ЗАДАНИЯ К ЛАБОРАТОРНОЙ РАБОТЕ №1

ПРОГРАММИРОВАНИЕ ЛИНЕЙНЫХ, РАЗВЕТВЛЯЮЩИХСЯ И ЦИКЛИЧЕСКИХ АЛГОРИТМОВ

Составить блок-схемы и программы к каждому из заданий.

В задании в) для организации цикла использовать оператор условного перехода.

ВАРИАНТ 1.

а) Дано х=2, у=-3.1

Вычислить: z=aSIN(b)-x^1/3, где а=COS³(x²-e²), b=(x+4)-y

б) Дано а=-0.5, b=2, t=0.324

Вычислить:

		at2Ln(t), если 1<=t2<=2
z=		1, если
		eatCOS(bt), если t2.2

в) Представить таблицу значений аргумента и заданной функции.

		х1/2+z, если z>0
у=
		ex-Ln(x), если z<=0

где z=COS(3x²-x+1) для х  [2;8] с шагом 0.5

Вариант 2

a) Дано: а=1.5, b=0.7, c=2.

Вычислить: z=SIN(xy)+2,

где

б) Вычислить:

		хLNx, если x>2
у=
		x2, если x<=2

z=COS²y³-e^Lgy для х=1.2, х=-5.3, х=4.2

в) Представить таблицу значений аргумента и заданной функции.

		, если x>0
z=		(2-x)c , если х=0
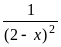		, если х>0

где b=e^(x+2)+0.6, c=x²-1 для х[-7;2] с шагом 2.

Вариант 3.

а) Дано: а=-2.7, b=4.1

Вычислить: y=xe^t-Lnxt, x=2SIN(a²b) - COS(a/b)

б) Вычислить: y=e^z+Lgz

		12-x, если x>0
z=		0 , если х=0
		COS4x, если х<0

для х=0.5, х=-2.73, х=5.1

в) Представить таблицу значений аргумента и заданной функции

		aSIN(x2+b), если x>0
y=		x2+b , если х=0
		bCOS(x2+a), если х<0

где a=2Tg(x), b=Arctg(x/18)-4 для x[7;17] с шагом h=2.

Вариант 4.

а) Вычислить:

где с=5.2, а=0.13, b=0.8

б) Вычислить: y=e^z+3.5-COS³(xz)

		1, если x>0
z=
		x2, если х<0

для х=3

в) Представить таблицу значений аргумента и заданной функции.

		3SIN(t)+Arctg(t), если t>-0.5
y=		(2t-et)/d , если t<-0.5
		bCOS(t)+a, если t=-0.5

где d=13e^t; a=0.5t³-SIN(t), b=1.5t-t^1/3

для t[-3.2;4.5] с шагом 0.9

Вариант 5.

a) Вычислить: у=х²-а²+Tg

где

для а=121.3, х=0.75, s=0.393

б) Вычислить:

		а(SIN(х)+COS2(x))+ea+bx, если bx3-65<a
y=		1-Ln((ax2-b))-x5, если bx3-65=a
		(x3-b)COS(3x-0.5), если bx3-65>a

a=15.631, b=3.084, x=0.194

в) Представить таблицу значений аргумента и заданной функции.

		aey, если y>1
z=
		Lny+5a, если y< =1

где а=COS(y-1) для у[-1;2] с шагом 0.3

ВАРИАНТ 6.

a) Дано: а=-1.7; b=2.4

Вычислить: z=e^x-SIN²(x+y),

где

б) Вычислить:

		х2/3-1, если х>=1
у=
		Lnх, если х<0

для х=1.2, х=-1.2, х=3.2

в) Представить таблицу значений аргумента и заданной функции.

		2COS(ux)/b, если u<0.1
z=		LnCOS(ux), если 0.1<=u<=2
		x2 COS(ux), если u>2

где x=COS²(u-2); b=SIN(u-2)² для u[-3.39;5.86] с шагом 0.93

ВАРИАНТ 7.

а) Дано: z=5.2, t=6.7, c=-2.5

Найти: y=4x²-Lgxz+c,

где

б) Вычислить: z=e^COS(xy)-2.7y

		0, если х>=0
у=
		x2+Lnх, если х<0

при х=-2, х=7.5, х=2.4

в) Представить таблицу значений аргумента и заданной функции .

		еz+x, если COS(х)>0.5
у=
		z-х, если COS(x)<=0.5

где для х[4;6] с шагом 0.2