5 Методические указания и пример к выполнению расчетного задания по развертке машин постоянного тока

По данным обмотки якоря, приведенным в таблице 5.1, требуется:

- вычислить шаги обмотки,

- начертить схему – развертку,

- показать напряжение тока в секциях и направление вращения якоря.

- определить шаг и максимальное число уравнительных соединений.

- показать несколько уравнительных соединений.

Таблица 5.1- Данные обмотки якоря

Вариант:	Тип обмотки	Z = k	2p	m (число контуров)
	Простая петлевая	24	6	1
	То же	22	4	1
	Сложная петлевая	28	6	2
	То же	22	4	2
	Простая волновая	21	4	1
	То же	28	6	1
	Сложная волновая	30	4	2
	То же	24	6	2
	Простая петлевая	32	4	1
	То же	24	4	1
	То же	32	6	1
	Простая волновая	24	4	1
	То же	17	4	1
	Сложная волновая	18	4	2
	Сложная петлевая	23	4	2
	То же	26	4	2
	Простая петлевая	27	6	1
	Простая волновая	21	4	1
	То же	27	4	1
	То же	18	4	1

Методические указания.

Выполнение схем – разверток обмоток, расположение полюсов и щеток производить аналогично примерам, приведенных в учебниках. Также следует показать уравнительные соединения обмоток варианта 3./2/

В подобных случаях обмотка выполняется с «мертвой» секцией. Число коллекторных пластин берется меньшим настолько, чтобы получить «у» равным целому числу. Секции не присоединенные к коллектору являются «мертвыми». В обмотках указанных вариантов берется по одной «мертвой» секции.

Вариант №10

Задание, по данным таблицы 5.2:

- вычислить шаги обмотки;

- начертить схему развертки;

- указать направление в секциях направление вращения якоря;

- начертить схему эл. соединения.

Таблица 5.2

Вариант:	Тип обмотки	Z = K	2p	m (число контуров)
10	Простая петлевая	24	4	1

Исходные данные:

Тип обмотки: простая петлевая.

Число зубьев якоря: Z = K = 24.

Число пар полюсов: 2p = 4.

Коэффициент сложности: m = 1.

Решение

Для симметричного расположения параллельных ветвей в магнитном поле необходимо, чтобы:

Z/а = ц.ч.;

2р/а = ц.ч.

Вычислим шаги обмотки (Рисунок 5.1):

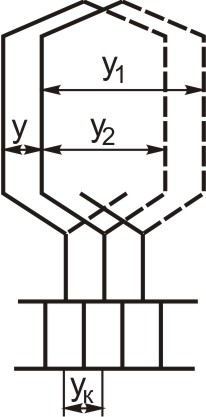
Рисунок 5.1 -Секции неперекрещенной, простой петлевой обмотки

Отличительным свойством простой петлевой обмотки является то, что для нее расстояние между данной и начальной секцией (результирующий шаг y) равен шагу коллектора y­­_к и равен 1:

.

Первый частичный шаг (шаг секции) определяется по формуле:

,

где: Z – число зубьев якоря,

2p – число пар полюсов,

 - дробь, при которой

y­₁ будет целым числом.

При ε = 0 шаг является полным.

Второй частичный шаг найдем из уравнения:

_,

_,

_.

_{Будем присваивать секционным сторонам номера тех элементарных пазов, в которых они лежат. Тогда по известным значениям шагов можно составить таблицу соединений секционных сторон обмотки, исходя из определенного элементарного паза и прибавляя к номеру этого паза значение первого частичного шага, значение второго шага, затем опять первого и т.д. Номера верхних сторон секций, изображенных сплошными линиями, проставлены в таблице сверху, а номера нижних сторон секций, изображенных штриховыми линиями, - снизу.}

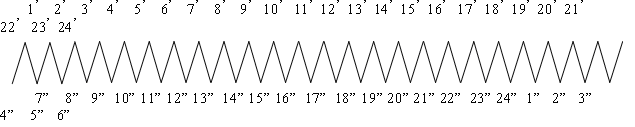
Рисунок 5.2 – Соединение секционных сторон простой петлевой обмотки

В секциях и во всей обмотке индуктируются переменные ЭДС. Как известно, синусоидальные ЭДС могут быть изображены на векторных диаграммах в виде векторов. Для изучения свойств якорных обмоток машин постоянного тока также целесообразно пользоваться подобными векторными диаграммами. Однако при этом ввиду несинусоидальной формы ЭДС проводников, витков и секций обмотки якоря необходимо рассматривать только основные гармоники этих ЭДС, т.е. первую гармонику.

Угол сдвига между ЭДС проводников соседних пазов

α =

Звезда пазовых ЭДС имеет Z векторов, но отдельные векторы могут совпадать по фазе, и число лучей поэтому может быть меньше Z, так как при построении звезды и обходе векторов ЭДС всех пазов совершается p полных оборотов. Если, например, Z/p= ц.ч., то и число лучей равно этой величине, и диаграмма состоит из p совпадающих или накладывающихся друг на друга звезд.

ЭДС проводников витка или проводников двух сторон секции сдвинуты на угол

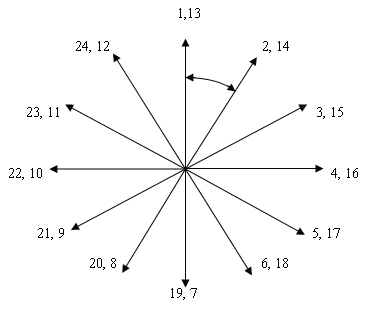Рисунок 5.3 – Векторная звезда ЭДС проводников всех пазов, при Z=24, 2p=4

α_с = , при _z =0, т.е. при полном шаге, векторы этих ЭДС сдвинуты на 180 .

Даже при соблюдении всех условий симметрии обмоток возможно нарушения равенства ЭДС параллельных ветвей из-за магнитной асимметрии или неравенства сопротивлений щеточного контакта отдельных щеточных болтов.

Чтобы уравнительные токи не загружали щеточный контакт, а замыкались внутри обмотки, выполняются специальные уравнительные соединения, связывающие равнопотенциальные точки обмотки якоря.

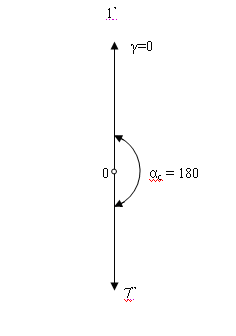
Рисунок 5.4 – Векторная диаграмма ЭДС секций 1^’ – 7^’’ , при z=24, p=4

Шаг уравнительных соединений равен:

,

Число уравнительных соединений равно:

,

Для простой петлевой обмотки 2а = 2р, тогда а = 2 .

Число уравнительных соединений применяется от одного на один паз, до 20% полного числа уравнительных соединений.

На рисунке 5.5 при выбранном положении якоря относительно полюсов получаются четыре параллельных ветви (2а = 2р = 4), где цифрами без штриха обозначены верхние секционные стороны, а цифрами со штрихом — нижние.

Рисунок 5.5 – Схема электрического соединения

6 Методические указания и примеры к выполнению задания по расчету трехфазного асинхронного двигателя, двигателей постоянного тока с параллельным и последовательным возбуждением и генератора постоянного тока