Синтез оптимального управления с полной обратной связью
Цель:Ознакомление с методикой построения линейных оптимальных систем управления с полной обратной связью методом динамического программирования Беллмана.
% Параметры системы
A=[3 0;1 -1]
B=[-1 3;1 0]
% Параметров критерия качества управления
Q=[1/2 0;0 1/2];
R=[1/2 0; 0 1/2];
% Время регулирования
T=10;
% Величина шага
SS=0.5;
% Количество шагов
N=T/SS
% Вычисление параметров регулятора
[k p e]= dlqr(A, B, Q, R)
x = zeros(2, N);
u= zeros(2, N-1);
% Начальные условия
x(1,1)=1;
x(2,1)=3;
% Построение графиков динамики системы
for i=1:N-1,
u(:, i)= - k*x(:, i);,
x(:, i+1)=A*x(:, i)+B*u(:, i);
end
x1= x(1,:);
x2= x(2,:);
t = 0:SS:T-SS;
subplot(4, 1, 1);
plot(t, x1, 'b');
subplot(4, 1, 2);
plot(t, x2, 'g');
subplot(4, 1, 3);
plot(SS:SS:T-SS, u(1, :), 'y');
subplot(4, 1, 4);
plot(SS:SS:T-SS, u(2, :), 'r');
k =
0.0617 -0.3498
0.8531 -0.0512
p =
4.7351 -1.3226
-1.3226 2.1176
e =
0.3109
-0.4588
Вывод: В данной работе мы ознакомились с методикой построения линейных оптимальных систем управления с полной обратной связью методом динамического программирования Беллмана.
В динамике система постепенно затухает, это мы можем наблюдать по графикам.
Контрольные вопросы
Сформулировать основную задачу оптимального управления. Оптимальное управление — это задача проектирования системы, обеспечивающей для заданного объекта управления или процесса закон управления или управляющую последовательность воздействий, обеспечивающих максимум или минимум заданной совокупности критериев качества системы.
Для решения задачи оптимального управления строится математическая модель управляемого объекта или процесса, описывающая его поведение с течением времени под влиянием управляющих воздействий и собственного текущего состояния. Математическая модель для задачи оптимального управления включает в себя: формулировку цели управления, выраженную через критерий качества управления; определение дифференциальных или разностных уравнений, описывающих возможные способы движения объекта управления; определение ограничений на используемые ресурсы в виде уравнений или неравенств.
формулируем задачу оптимального управления:
Уравнения
состояния:
(1).
Граничные
условия
,
(2).
Минимизируемый
функционал:
.
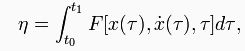здесь
x(t)
— вектор состояния , u(t)
— управление,
—
начальный и конечный моменты времени.
Задача
оптимального управления заключается
в нахождении функций состояния и
управления для времени
,
которые минимизируют функционал.
Дать определение критерия качества.
Для того, что сформулировать задачу оптимального управления, необходимо задать условие, которое позволяет отличать друг от друга более и менее выгодные решения данной задачи. Этой цели служит критерий оптимальности (критерий качества управления или целевой функционал)
Вывести необходимое условие оптимальности.
Теорема (Вейерштрасса). Для того, чтобы в задаче (2.3.1) существовала точка глобального максимума (минимума), достаточно, чтобы допустимое множество X было компактно в Rn, а целевая функция f непрерывна на X.