5. Вычисление показателей надежности и риска системы при наличии восстановления

Предположим, что количество ремонтных органов достаточно для того, чтобы подсистемы были независимы по восстановлению (неограниченное восстановление). В этом случае можно воспользоваться формулами (1.11) и (1.12). Поскольку восстановление элементов значительно повышает надежность системы и снижает риск из-за отказа элементов, то в каждой резервной группе можно оставить лишь по одному резервному элементу. Таким образом, для ремонтируемой системы ее структурная схема имеет вид, показанный на рисунке 5.

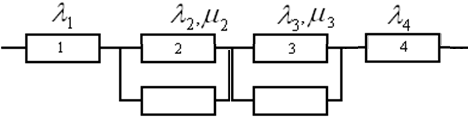
Рисунок 5 – Структурная схема восстанавливаемой системы

1. Постоянно включенный резерв

Поскольку первая и четвёртая подсистемы являются нерезервированными, а вторая и третья представляют собой дублированные подсистемы, то в соответствии с формулой (1.7) для постоянно включенного резерва получим следующие формулы для вероятности безотказной работы подсистем:

, , , ,

где:

, ,

, ,

- интенсивность восстановления элементов -й подсистемы,

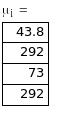
Теперь для вычисления показателей надежности системы можно воспользоваться соотношением (1.11). В результате получим:

.

Расчеты с помощью системы MathCAD показывают, что:

Аналогично, используя (1.2), найдем риск системы в момент :

2. Резерв замещением

В соответствии с формулой (1.9) для резерва замещением получим следующие формулы для вероятности безотказной работы подсистем:

, , , ,

где

, ,

, ,

- интенсивность восстановления элементов -й подсистемы,

Теперь для вычисления показателей надежности системы можно воспользоваться соотношением (1.11). В результате получим:

,

Расчеты с помощью системы MathCAD показывают, что:

Аналогично, используя (1.12), найдем риск системы в момент :

6. Определение показателей надежности и суммарного риска усовершенствованной системы

Ориентированный граф состояний ремонтируемой системы с постоянно включенным резервом изображен на рисунке 6. Он имеет 21 узел. Направление стрелок сверху вниз соответствует отказовым переходам, а снизу вверх – восстановлению элементов. На графе кружками отмечены исправные состояния, а квадратами – отказовые.

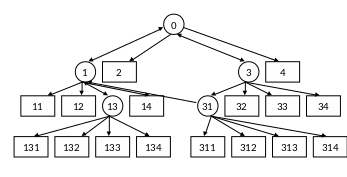
Рисунок 6 – Граф состояний восстанавливаемой системы

Интенсивности отказового перехода из каждого узла равны соответственно , , , , умноженным на число исправных элементов данной резервной группы. Интенсивности ремонта для четвертой и пятой подсистем равны соответственно и . Согласно заданной дисциплине обслуживания первыми восстанавливаются элементы четвертой подсистемы, а затем – элементы пятой подсистемы.

Для удобства записи уравнений пронумеруем узлы графа в естественном порядке. Тогда узлы (0), (1), (3), (7), (9) соответствуют исправным, а остальные узлы – отказовым состояниям. По графу составляется система обыкновенных дифференциальных уравнений, которая в данном случае имеет вид:

Считая, что при все элементы системы исправны, получаем начальные условия: , , .

Необходимо привести значения интенсивности переходов к одной размерности. Для этого следует интенсивности восстановления элементов умножить на 8760, что соответствует переводу 1 часа в годы.

Поэтому

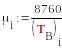
Систему уравнений решим численно с использованием метода Рунге-Кутты.

Метод состоит в следующем:

Определим начальные значения искомой функции

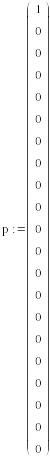
• Запишем уравнения:

• Находим решение с помощью следующей функции:

Z= Radau (p,x₁,x₂,n,D),

где

p - вектор начальных условий

x₁,x₂ - границы интервала для поиска решения

n - количество точек на интервале

D(x,y) - вектор-функция первых производных.

В нашем случае:

В результате получим:

Таблица 2. Вероятности и их значения

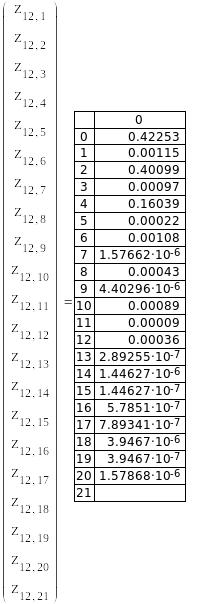
Таблица 3. Вероятность безотказной работы системы

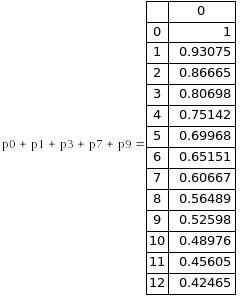
Для определения наработки на отказ составим следующую систему линейных алгебраических уравнений:

Для численного решения линейных систем уравнений в MathCAD имеется специальная функция:

Lsolve(A,B). Она решает систему линейных алгебраических уравнений вида A x X=B, выдавая решение – вектор Х .

А- матрица коэффициентов размерности (n x n);

B- вектор свободных членов размерности n;

Х-вектор неизвестных пока решений.

В нашем случае:

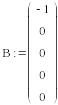
Решение этой системы дает следующие результаты:

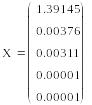
Следовательно, среднее время безотказной работы равно:

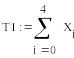
Найдем суммарный риск системы в соответствии с формулой (1.18). Для этого по графу необходимо найти все состояния отказа и для каждого из них определить номер элемента, отказ которого привет к отказу системы. Соответствие отказов состояний и номеров отказавших элементов приведено в таблице 4.

Таблица 4. Номер элемента и состояний

Номер состояния	Номер элемента	Номер состояния	Номер элемента
2	2	16	4
4	4	17	1
5	1	18	2
6	2	19	3
8	4	20	4
10	2	-	-
11	3	-	-
12	4	-	-
13	1	-	-
14	2	-	-
15	3	-	-

По формуле 1.18 получим:

R(1.2)= 29.6965

Выводы

По результатам проведенных исследований составлена таблица 5, в которой содержатся значения показателей надежности и риска системы для постоянно включенного резерва.

Таблица 5. Значения показателей надежности и риска резервированной системы

Система	Показатели надежности		Риск системы R(1.2)
	P(1.2)	Т1,лет
Неремонтируемая	0.3606	1.1765	42.9028
Ремонтируемая (неограниченное восстановление)	0.43145	1.4275	32.597
Ремонтируемая (ограниченное восстановление)	0.4316	1.428	29.6965

Из сводной таблицы видно, что при использовании неремонтируемой системы увеличивается риск системы, но при этом уменьшается вероятность безотказной работы системы и среднее время безотказной работы, по отношению к двум другим системам.

Резервирование повышает надежность системы. Это видно из следующих данных:

вероятность безотказной работы нерезервированной системы Р(1.2)= 0.3606, ниже чем для резервированной системы Р(1.2)= 0.43145; среднее время безотказной работы системы нерезервированной системы Т₁=1.1765 ниже, чем при резервированной системы Т₁=1.4275, риск нерезервированной системы R(1.2)= 42.9028 выше, чем у резервированной системы R(1.2)= 29.6965.

Также был рассмотрен метод повышения надежности при помощи восстановления отказавших элементов.

Восстановление- это событие, заключающее в переходе объекта из неработоспособного в работоспособное состояние, в результате устранения отказа путем перестройки структуры, ремонта или замены отказавших частей.

Из таблицы видно, что система неремонтируемая имеет больший риск, по сравнению с ремонтируемыми системами, причем с неограниченным восстановлением риск больше, чем с ограниченным восстановлением. Возможность ремонта элементов приводит к уменьшению кратности резервирования и сокращению объема оборудования.

Вар.	n	m	t, лет	Характ.	Элем. 1	Элем. 2	Элем. 3	Элем. 4	Элем. 5
1	4	110	1,9	Т, лет	12	2	16	2	−
				Тв, час	24	24	120	50	−
				r, у. е.	1000	30	1000000	20	−

Вар.	n	m	t, лет	Характ.	Элем. 1	Элем. 2	Элем. 3	Элем. 4	Элем. 5
2	4	90	1,8	Т, лет	10	16	5	3	−
				Тв, час	120	240	60	90	−
				r, у. е.	10000	1000000	30	30	−

Вар.	n	m	t, лет	Характ.	Элем. 1	Элем. 2	Элем. 3	Элем. 4	Элем. 5
3	4	110	2	Т, лет	5	3	16	14	−
				Тв, час	100	100	240	100	−
				r, у. е.	50	30	100000	1000	−

Вар.	n	m	t, лет	Характ.	Элем. 1	Элем. 2	Элем. 3	Элем. 4	Элем. 5
4	5	110	1,6	Т, лет	14	4	5	18	5
				Тв, час	120	96	20	200	24
				r, у. е.	10000	10	40	100000	40

Вар.	n	m	t, лет	Характ.	Элем. 1	Элем. 2	Элем. 3	Элем. 4	Элем. 5
5	4	100	1,9	Т, лет	14	20	3	4	−
				Тв, час	100	200	50	50	−
				r, у. е.	1000	100000	10	20	−

Вар.	n	m	t, лет	Характ.	Элем. 1	Элем. 2	Элем. 3	Элем. 4	Элем. 5
6	4	120	1,1	Т, лет	2	16	14	5	−
				Тв, час	50	200	120	90	−
				r, у. е.	40	1000000	10000	40	−

Вар.	n	m	t, лет	Характ.	Элем. 1	Элем. 2	Элем. 3	Элем. 4	Элем. 5
7	5	120	1,4	Т, лет	4	18	12	5	2
				Тв, час	30	200	100	50	40
				r, у. е.	30	100000	1000	50	10

Вар.	n	m	t, лет	Характ.	Элем. 1	Элем. 2	Элем. 3	Элем. 4	Элем. 5
8	4	80	1,2	Т, лет	2	14	10	2	−
				Тв, час	60	180	96	40	−
				r, у. е.	30	100000	1000	30	−

Вар.	n	m	t, лет	Характ.	Элем. 1	Элем. 2	Элем. 3	Элем. 4	Элем. 5
9	4	80	1,1	Т, лет	4	10	2	14	−
				Тв, час	70	200	50	180	−
				r, у. е.	30	1000	10	100000	−

Вар.	n	m	t, лет	Характ.	Элем. 1	Элем. 2	Элем. 3	Элем. 4	Элем. 5
10	4	120	1,5	Т, лет	3	12	12	4	−
				Тв, час	40	150	120	90	−
				r, у. е.	50	100000	10000	40	−

27