§6.Числовые характеристики системы двух случайных величин.
Для описания системы двух случайных величин кроме математических ожиданий и дисперсий составляющих используют и другие характеристики; к их числу относятся корреляционный момент и коэффициент корреляции.
Условное математическое ожидание в теории вероятностей - это среднее значение случайной величины относительно условного распределения.
Будем
считать, что дано вероятностное
пространство
.
Пусть
- интегрируемая случайная величина, то
есть
.
Пусть также
- под-σ-алгебра
σ-алгебры
.
УМО относительно σ-алгебры
Случайная
величина 
называется
условным математическим
ожиданием 
относительно
σ-алгебры 
,
если
измерима относительно .
,
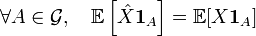где 
- индикатор события 
.
Условное математическое ожидание
обозначается 
.
Пример. Пусть 
Положим 
.
Тогда
-
σ-алгебра, и
.
Пусть случайная величина
имеет
вид
.
Тогда
УМО относительно семейства событий
Пусть 
-
произвольное семейство событий. Тогда
условным математическим
ожиданием
относительно 
называется
,
где 
-
минимальная сигма-алгебра, содержащая
.
Пример. Пусть
Пусть
также 
.
Тогда 
.
Пусть случайная величина
имеет
вид
.
Тогда
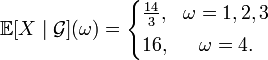
УМО относительно случайной величины
Пусть 
другая
случайная величина. Тогда условным
математическим ожиданием
относительно 
называется
,
где 
-
σ-алгебра, порождённая случайной
величиной
.
Условная вероятность
Пусть 
-
произвольное событие, и 
-
его индикатор. Тогда условной
вероятностью 
относительно
называется
.
Корреляционным
моментом
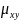случайных
величин
и
называют математическое ожидание
произведения отклонений этих величин:
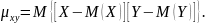
Для вычисления корреляционного момента дискретных величин используют формулу
а для непрерывных величин—формулу
Корреляционный момент служит для характеристики связи между величинами и . Как будет показано ниже, корреляционный момент равен нулю, если и независимы; следовательно, если корреляционный момент не равен нулю, то и — зависимые случайные величины.
Замечание 1. Учитывая, что отклонения есть центрированные случайные величины корреляционный момент можно определить как математическое ожидание произведения центрированных случайных величин:
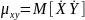
Замечание 2. Легко убедиться, что корреляционный момент можно записать в виде
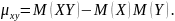
Теорема 1. Корреляционный момент двух независимых случайных величин X и Y равен нулю.
Из определения корреляционного момента следует, что он имеет размерность, равную произведению размерностей величин и . Другими словами, величина корреляционного момента зависит от единиц измерения случайных величин. По этой причине для одних и тех же двух величин величина корреляционного момента имеет различные значения в зависимости от того, в каких еди- ницах были измерены величины.
Пусть,
например,
и
были измерены в сантиметрах и
;
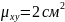если измерить
и
в миллиметрах, то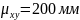
.
Такая особенность корреляционного
момента является недостатком этой
числовой характеристики, поскольку
сравнение корреляционных моментов
различных систем случайных величин
становится затруднительным. Для того
чтобы устранить этот недостаток, вводят
новую числовую характеристику—коэффициент
корреляции.
Коэффициентом
корреляции
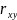случайных величин
и
называют отношение корреляционного
момента к произведению средних
квадратических отклонений этих величин:
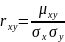
Так
как размерность
равна произведению размерностей величин
и
,
имеет размерность величины
,
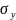имеет размерность величины
, то
—безразмерная
величина. Таким образом, величина
коэффициента корреляции не зависит от
выбора единиц измерения случайных
величин. В этом состоит преимущество
коэффициента корреляции перед
корреляционным моментом.
Очевидно,
коэффициент корреляции независимых
случайных величин равен нулю (так как
.
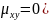Замечание
3. Во многих
вопросах теории вероятностей целесообразно
вместо случайной величины
рассматривать нормированную случайную
величину
,
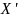которую определяют как отношение
отклонения к среднему квадратическому
отклонению:
Теорема 2. Абсолютная величина корреляционного момента двух случайных величин X и Y не превышает среднего геометрического их дисперсий:
Теорема 3. Абсолютная величина коэффициента корреляции не превышает единицы:
