§4.Плотность распределения двумерной случайной величины

Двумерная случайная величина задавалась с помощью функции распределения. Непрерывную двумерную величину можно также задать, пользуясь плотностью распределения. Здесь и далее будем предполагать, что функция распределения 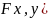всюду непрерывна и имеет всюду (за исключением, быть может, конечного числа кривых) непрерывную частную производную второго порядка.

Плотностью совместного распределения вероятностей 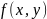двумерной непрерывной случайной величины (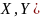 называют вторую смешанную частную производную от функции распределения:

Геометрически эту функцию можно истолковать как поверхность, которую называют поверхностью распределения.

Пример. Найти плотность совместного распределения системы случайных величин по известной функции распределения

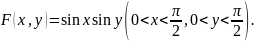
Решение. По определению плотности совместного распределения.

Найдем частную производную по х от функции распределения:

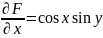
Найдем от полученного результата частную производную по , в итоге получим искомую плотность совместного распределения:

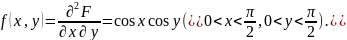
Свойства двумерной плотности вероятности

Свойство 1. Двумерная плотность вероятности неотрицательна:

Доказательство. Вероятность попадания случайной точки в прямоугольник со сторонам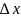и: и 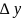есть неотрицательное число; площадь этого прямоугольника — положительное число. Следовательно, отношение этих двух чисел, а значит, и их предел (пр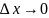и и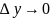 ), который равен есть неотрицательное число, т. е.

Заметим, что свойство непосредственно следует из того, что — неубывающая функция своих аргументов.

Свойство 2. Двойной несобственный интеграл с бесконечными пределами от двумерной плотности равен единице:

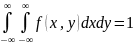
Доказательство. Бесконечные пределы интегрирования указывают, что областью интегрирования служит вся плоскость ; поскольку событие, состоящее в том, что случайная точка попадет при испытании на плоскость , достоверно, то вероятность этого события (она и определяется двойным несобственным интегралом от двумерной плотности) равна единице, т. е.

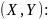
Пример. Задана плотность совместного распределения непрерывной двумерной случайной величины 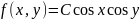в квадрате 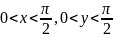; вне этого квадрата Найти постоянный параметр

Решение. Воспользуемся свойством 2, учитывая, что изменяются от 0 до :

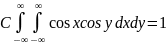
Отсюда

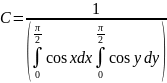
Выполнив интегрирование, получим искомое значение параметра .

§5.Условные законы распределения составляющих системы дискретных случайных величин

Известно, что если события и 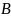зависимы, то условная вероятность события отличается от его безусловной вероятности. В этом случае

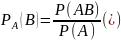
Аналогичное положение имеет место и для случайных величин. Для того чтобы охарактеризовать зависимость между составляющими двумерной случайной величины, введем понятие условного распределения.

Рассмотрим дискретную двумерную случайную величину 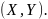Пусть возможные значения составляющих таковы: .

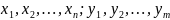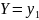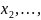Допустим, что в результате испытания величина приняла значение ; при этом примет одно из своих возможных значений: , или или 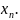Обозначим условную вероятность того, что примет, например, значение при условии, что , через . Эта вероятность, вообще говоря, не будет равна безусловной вероятности :

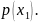
В общем случае условные вероятности составляющей будем обозначать так:

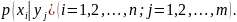
Условным распределением составляющей при 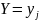называют совокупность условных вероятностей 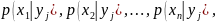вычисленных в предположении, что событие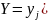 имеет одно и то же значение при всех значениях ) уже наступило. Аналогично определяется условное распределение составляющей .

Зная закон распределения двумерной дискретной случайной величины, можно, пользуясь формулой (*), вычислить условные законы распределения составляющих. Например, условный закон распределения в предположении, что событие уже произошло, может быть найден пo формуле

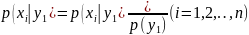
В общем случае условные законы распределения составляющей X определяются соотношением

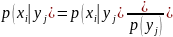
Аналогично находят условные законы распределения составляющей :

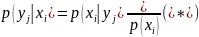
Замечание. Сумма вероятностей условного распределения равна единице. Действительно, так как при фиксированном имеем

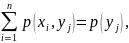
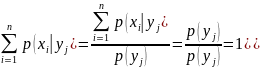
Аналогично доказывается, что при фиксированном

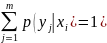
Это свойство условных распределений используют для контроля вычислений.

Пример. Дискретная двумерная случайная величина задана табл. 6.

Таблица6

	0,10	0,30	0,20
	0,06	0,18	0,16

Найти условный закон распределения составляющей при условии, что составляющая приняла значение .

Решение. Искомый закон определяется совокупностью следующих условных вероятностей:

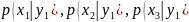
Воспользовавшись формулой (*) и приняв во внимание, что 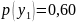, имеем:

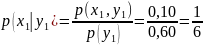
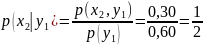
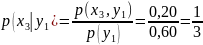
Сложив для контроля найденные условные вероятности, убедимся, что их сумма равна единице, как и должно быть, в соответствии с замечанием, помещенным выше: .

Условные законы распределения составляющих системы непрерывных случайных величин

Пусть (X, Y) — непрерывная двумерная случайная величина.

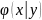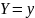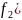Условной плотностью распределения составляющих при данном значении называют отношение плотности совместного распределения системы к плотности распределения ) составляющей :

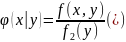
Подчеркнем, что отличие условной плотности от безусловной плотности 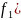) состоит в том, что функция дает распределение при условии, что составляющая приняла значение 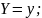функция же 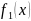дает распределение независимо от того, какие из возможных значений приняла составляющая .

Аналогично определяется условная плотность составляющей при данном значении :

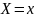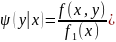
Если известна плотность совместного распределения 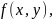то условные плотности составляющих могут быть найдены в силу (*) и (**) по формулам:

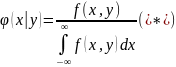
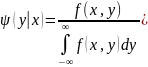
Запишем формулы (*) и (**) в виде

)

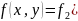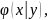
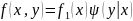
Отсюда заключаем: умножая закон распределения одной из составляющих на условный закон распределения другой составляющей, найдем закон распределения системы случайных величин.

Как и любая плотность распределения, условные плотности обладают следующими свойствами: