§3. Функция распределения двумерной случайной величины.

Рассмотрим двумерную случайную величину (безразлично, дискретную или непрерывную).

Пусть —пара действительных чисел. Вероятность события, состоящего в том, что примет значение, меньшее и при этом примет значение, меньшее , обозначим через Если и будут изменяться, то, вообще говоря, будет изменяться и т. е. есть функция от и .

Функцией распределения двумерной случайной величины называют функцию определяющую для каждой пары чиселx вероятность того, что примет значение, меньшее , и при этом примет значение, меньшее :

Геометрически это равенство можно истолковать так: есть вероятность того, что случайная точка попадет в бесконечный квадрант с вершиной , расположенный левее и ниже этой вершины (рис. 1).

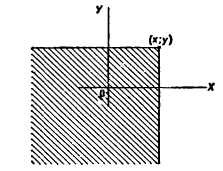
Рис 1.

Пример. Найти вероятность того, что в результате испытания составляющая двумерной случайной величины примет значение и при этом составляющая примет значение , если известна функция распределения системы

Решение. По определению функции распределения двумерной случайной величины,

Положив получим искомую вероятность

= .

Свойства функции распределения двумерной случайной величины

Свойство 1. Значения функции распределения удовлетворяют двойному неравенству

Доказательство. Свойство вытекает из определения функции распределения как вероятности: вероятность— всегда неотрицательное число, не превышающее единицу.

Свойство 2. есть неубываюищя функиия по каждому аргументу, т.е.

Доказательство. Докажем, что — неубывающая функция по аргументу . Событие, состоящее в том, что составляющая примет значение, меньшее , и при этом составляющая , можно подразделить на следующие два несовместных события:

1. примет значение, меньшее , и при этом с вероятностью ;

2. примет значение, удовлетворяющее неравенству , и при этом с вероятностью

По теореме сложения,

Отсюда

или

Любая вероятность есть число неотрицательное, поэтому

что и требовалось доказать.

Свойство становится наглядно ясным, если воспользоваться геометрическим истолкованием функции распределения как вероятности попадания случайной точки в бесконечный квадрант с вершиной (рис. 1). При возрастании х правая граница этого квадранта сдвигается вправо; при этом вероятность попадания случайной точки в «новый» квадрант, очевидно, не может уменьшиться.

Аналогично доказывается, что есть неубывающая функция по аргументу .

Свойство 3. Имеют место предельные соотношения:

1)

3) .

Доказательство. 1) есть вероятность события и ; но такое событие невозможно (поскольку невозможно событие ), следовательно, вероятность этого события равна нулю.

Свойство становится наглядно ясным, если прибегнуть к геометрической интерпретации: при , правая граница бесконечного квадранта (рис. 1) неограниченно сдвигается влево и при этом вероятность попадания случайной точки в квадрант стремится к нулю.

2) Событие , невозможно, поэтому )=0,

3) Событие , и Y , невозможно, поэтому )=0.

4) Событие , и , достоверно, следовательно, вероятность этого события .

Свойство становится наглядно ясным, если принять во внимание, что при , и , бесконечный квадрант (рис. 1) превращается во всю плоскость и, следовательно, попадание случайной точки ( в эту плоскость есть достоверное событие.

Свойство 4. а) При функция распределения системы становится функцией распределения составляющей :

б) При функция распределения системы становится функцией распределения составляющей :

Доказательство. а) Так как событие Y достоверно, то определяет вероятность события , т. е. представляет собой функцию распределения составляющей .

б) Доказывается аналогично.