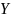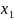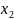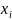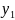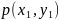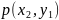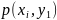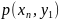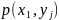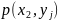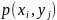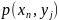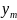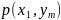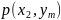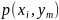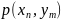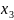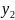Приднестровский государственный университет им. Т.Г. Шевченко

Инженерно-технический институт

Кафедра программного обеспечения вычислительной техники

и автоматизированных систем

РЕФЕРАТ

по дисциплине

«Теория вероятностей и математическая статистика»

Тема: «Двумерные случайные величины»

Работу выполнил

студент группы ИТ11ДР62ИВ1

Дурбайлов Иван

Тирасполь, 2012год.

СОДЕРЖАНИЕ

§2. Закон распределения дискретной двумерной случайной величины.

§3. Функция распределения двумерной случайной величины.

§4.Плотность распределения двумерной случайной величины

§5.Условные законы распределения составляющих системы дискретных случайных величин

§6.Числовые характеристики системы двух случайных величин.

§7.Зависимые и независимые случайные величины

Пусть на вероятностном пространстве Ω заданы две случайные величины: 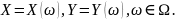 Каждому элементарному событию Ω ставится в соответствие упорядоченная пара значений   случайных величин X,Y.

Упорядоченную пару 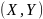   двух одномерных случайных величин   называют двумерной случайной величиной.

Двумерную случайную величину называют также случайным двумерным вектором, случайной двумерной точкой, системой двух случайных величин. Одномерные случайные величины   называются компонентами двумерной случайной величины  .

§2. Закон распределения дискретной двумерной случайной величины.

Двумерная случайная величина  . называется дискретной, если множество ее значений 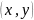  – конечное или счетное.

Закон распределения вероятностей двумерной дискретной случайной величины  . можно задать формулой

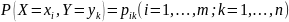(3)

События 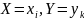  образуют полную группу событий, поэтому сумма всех вероятностей

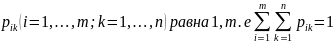(4)

Законом распределения дискретной двумерной случайной величины называют перечень возможных значений этой величины, т. е. пар чисел 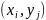и их вероятностей 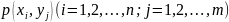. Обычно закон распределения задают в виде таблицы с двойным входом (табл. 1).

Первая строка таблицы содержит все возможные значения составляющей 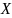, а первый столбец — все возможные значения составляющей Y. В клетке, стоящей на пересечении «столбца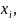 » и «строк 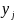», указана вероятность 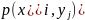того, что двумерная случайная величина примет значение .

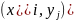Так как события 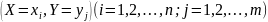образуют полную группу то сумма вероятностей, помещенных во всех клетках таблицы, равна единице.

Таблица 1

			…		…
…	…	…	…	…	…	…
…	…	…	…	…	…	…
			…		…

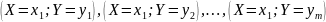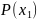Зная закон распределения двумерной дискретной случайной величины, можно найти законы распределения каждой из составляющих. Действительно, например, события несовместны, поэтому вероятность того, что примет значение по теореме сложения такова:

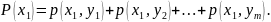
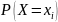Таким образом, вероятность того, что примет значение , равна сумме вероятностей «столбца ». В общем случае, для того чтобы найти вероятность , надо просуммировать вероятности столбца . Аналогично сложив вероятности «строки », получим вероятность .

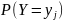Пример. Найти законы распределения составляющих двумерной случайной величины, заданной законом распределения (табл. 2).

Таблица 2

	0,10	0,30	0,20
	0,06	0,18	0,16

Решение. Сложив вероятности по столбцам, получим вероятности возможных значений :

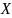Напишем закон распределения составляющей :

Таблица 4

	0,16	0,48	0,36

Контроль: 0,16+0,48+0,36=1.

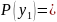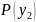Сложив вероятности по строкам, получим вероятности возможных значений : 0,60; =0,40. Напишем закон распределения составляющей :

Таблица 5

	0,60	0,40