Построение графов, матриц примыканий списка примыканий

Граф – множество вершин (узлов), соединенных ребрами (дугами). Обозначение графа: G = (V, E), где V – множество вершин, E – множество дуг.

Ориентированный граф – граф, ребра в котором имеют направление, т.е. являются дугами.

Взвешенный граф – граф, ребра которого имеют вес, то есть числовое или логическое значение. В нашем случае весом являются интенсивность в приведенных единицах.

Матрица примыканий – двумерный массив, в котором по вертикали указывается исходные вершины, по горизонтали – конечные. В ячейках матрицы ориентированного графа ставится 0, если из соответствующей исходной вершины нельзя пройти в соответствующую конечную вершину, и 1, если из соответствующей исходной вершины можно пройти в соответствующую конечную вершину.

Ячейка матрицы взвешенного графа содержит знак бесконечности ∞, если ребро отсутствует. Во всех остальных случаях значение ячейки равно весу.

Главная диагональ матрицы содержит нули.

Список примыканий содержит все вершины графа; каждая вершина представляет собой динамически формируемый список вершин, примыкающей к ней.

Ориентированный граф:

ул. Московское шоссе х ул. Революционная

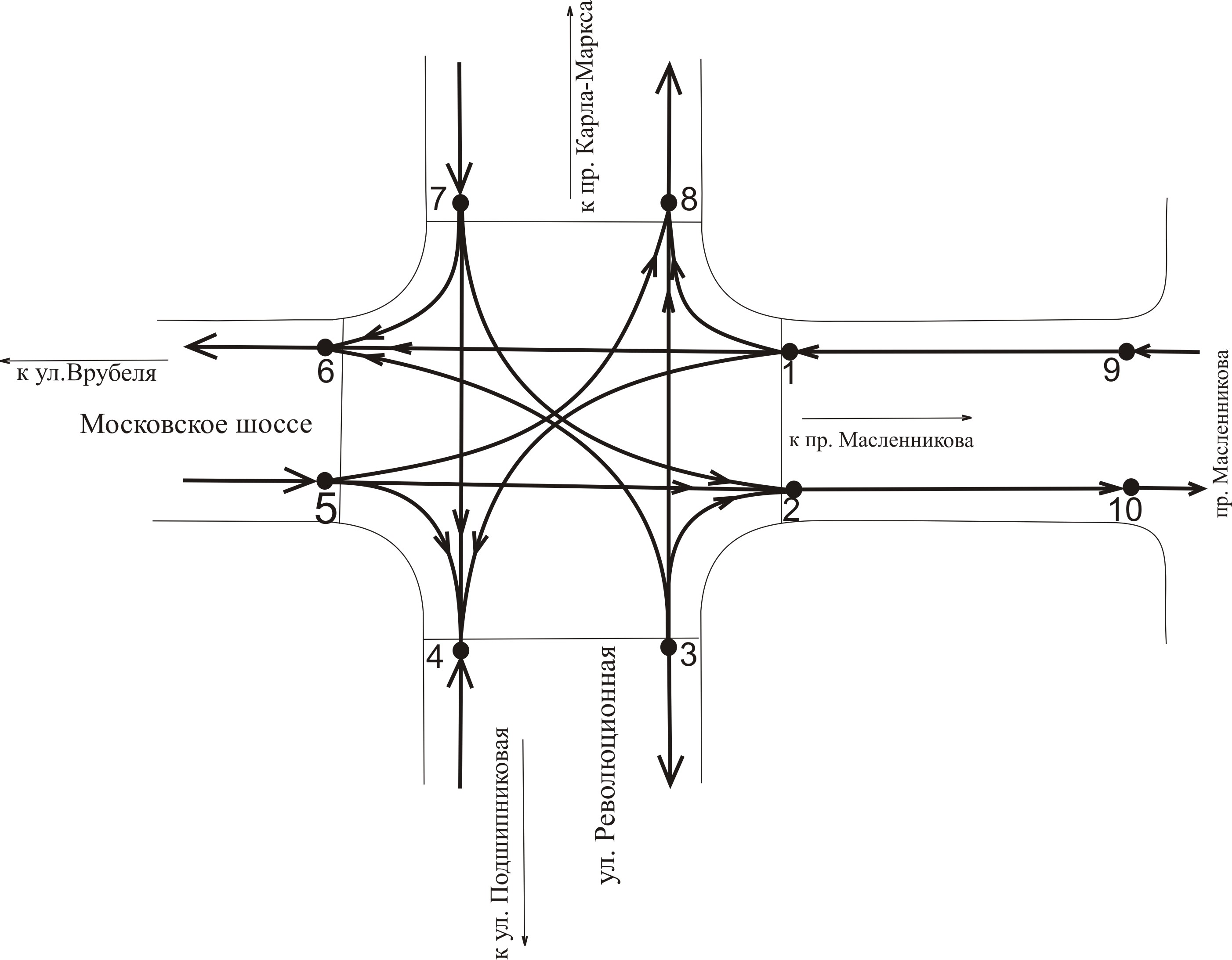
Рисунок 4. Ориентированный граф

Взвешенный граф:

ул. Московское шоссе х ул. Революционная

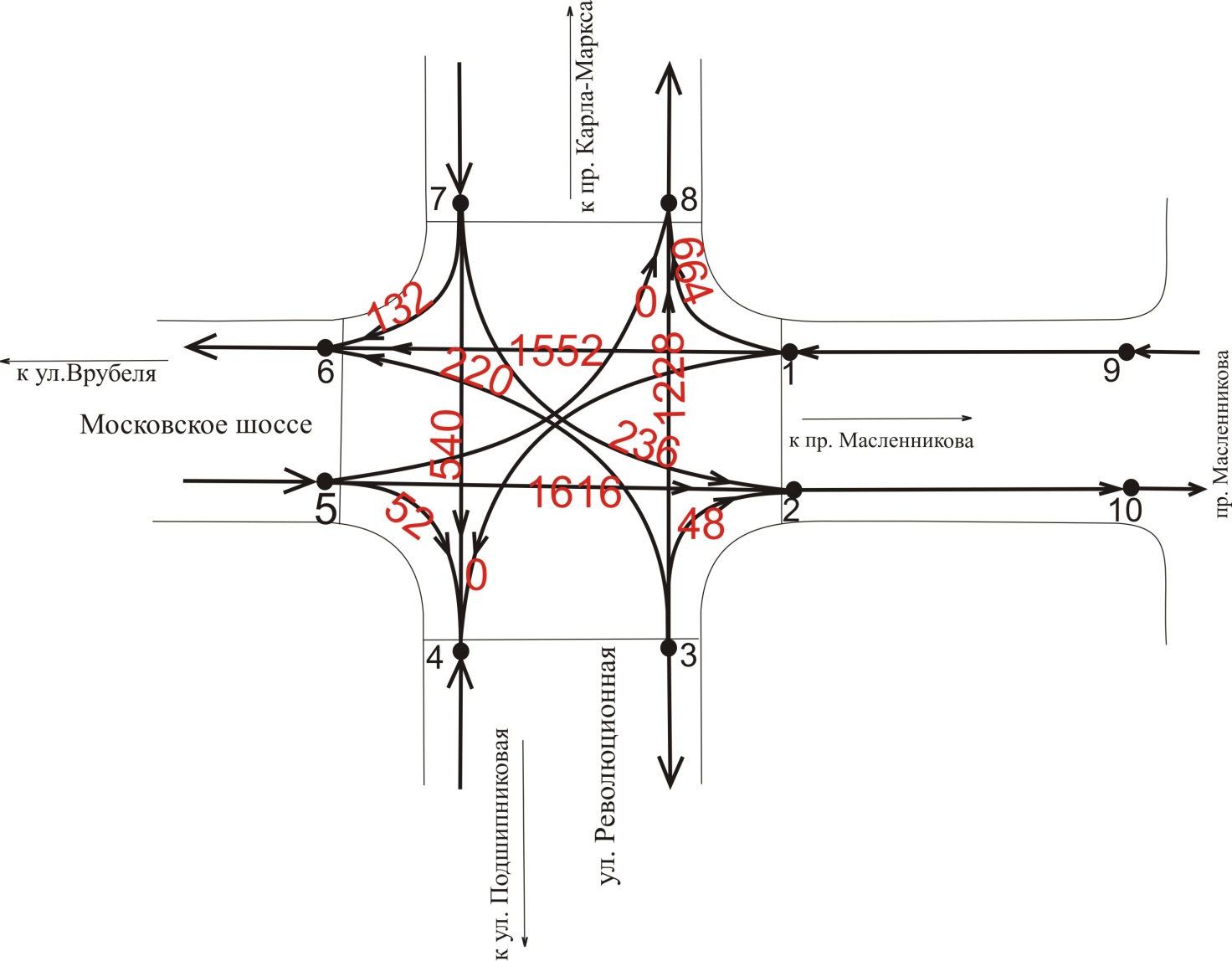
Рисунок 5. Взвешенный граф

Матрицы примыканий:

ул. Московское шоссе х ул. Революционная

Таблица 11 – матрица примыкания орграфа

	1	2	3	4	5	6	7	8	9	10
1	0	0	0	1	0	1	0	1	0	0
2	0	0	0	0	0	0	0	0	0	1
3	0	1	0	0	0	1	0	1	0	0
4	0	0	0	0	0	0	0	0	0	0
5	0	1	0	1	0	0	0	1	0	0
6	0	0	0	0	0	0	0	0	0	0
7	0	1	0	1	0	1	0	0	0	0
8	0	0	0	0	0	0	0	0	0	0
9	1	0	0	0	0	0	0	0	0	0
10	0	0	0	0	0	0	0	0	0	0

ул. Московское шоссе х ул. Революционная

Таблица 12 – матрица примыкания взвешенного графа

	1	2	3	4	5	6	7	8	9	10
1	0	∞	∞	0	∞	1552	∞	664	∞	∞
2	∞	0	∞	∞	∞	∞	∞	∞	∞	I
3	∞	48	0	∞	∞	220	∞	1228	∞	∞
4	∞	∞	∞	0	∞	∞	∞	∞	∞	∞
5	∞	1616	∞	52	0	∞	∞	0	∞	∞
6	∞	∞	∞	∞	∞	0	∞	∞	∞	∞
7	∞	236	∞	540	∞	132	0	∞	∞	∞
8	∞	∞	∞	∞	∞	∞	∞	0	∞	∞
9	I	∞	∞	∞	∞	∞	∞	∞	0	∞
10	∞	∞	∞	∞	∞	∞	∞	∞	∞	0