
- •1.Прочность,жесткость, устойчивость
- •3.Типы элементов сооружений.
- •Этапы метода сечений
- •6.Какой вид нагружения называется растяжением-сжатием
- •7.Каким методом строятся эпюры внутренних силовых факторов?Применение на примере построения эпюры продольных сил
- •8.Напряжения в поперечных сечениях стержня при растяжении-сжатии Напряжения
- •9.Эпюры внутренних усилий при растяжении-сжатии
- •10.Механические испытания Испытание на растяжение
- •11.Условие прочности при растяжении сжатии
- •12.Деформации при растяжении-сжатии
Этапы метода сечений
Метод сечений состоит из четырех последовательных этапов: разрезать, отбросить, заменить, уравновесить.
1.Разрежем стержень,
находящийся в равновесии под действием
некоторой системы сил![]() (рис.
1.3, а) на две части плоскостью,
перпендикулярной к его оси z.
(рис.
1.3, а) на две части плоскостью,
перпендикулярной к его оси z.
2.Отбросим одну из частей стержня и рассмотрим оставленную часть.
3.Поскольку мы как бы разрезали бесчисленное множество пружинок, соединявших бесконечно близкие частицы тела, разделенного теперь на две части, в каждой точке поперечного сечения стержня необходимо приложить силы упругости, которые при деформации тела возникли между этими частицами. Иными словами, заменимдействие отброшенной части внутренними силами (рис. 1.3, б).
ВНУТРЕННИЕ СИЛЫ В МЕТОДЕ СЕЧЕНИЙ
1.Полученную бесконечную систему сил по правилам теоретической механики можно привести к центру тяжести поперечного сечения. В результате получим главный вектор R и главный момент M (рис. 1.3, в).
2.Разложим главный вектор и главный момент на составляющие по осям x, y (главные центральные оси) и z.
3.Получим
6 внутренних
силовых факторов,
возникающих в поперечном сечении стержня
при его деформировании: три силы ![]() (рис.
1.3, г) и три момента
(рис.
1.3, г) и три момента ![]() (рис.
1.3, д).
(рис.
1.3, д).
Сила N - продольная сила
![]() –
поперечные
силамы,
–
поперечные
силамы,
момент
относительно оси z (![]() )
– крутящий момент
)
– крутящий момент
моменты
относительно осей x, y (![]() )
– изгибающие моменты.
)
– изгибающие моменты.
Запишем для оставленной части тела уравнения равновесия (уравновесим):
![]() .
.
Из
уравнений определяются внутренние
усилия, возникающие в рассматриваемом
поперечном сечении стержня.
ВЫЧИСЛЕНИЕ ПРОДОЛЬНОЙ И ПОПЕРЕЧНЫХ СИЛ, КРУТЯЩЕГО И ИЗГИБАЮЩИХ МОМЕНТОВ
продольная сила N равна сумме проекций всех сил (активных и реактивных), действующих на любую из частей рассеченного стержня, на ось z;поперечные силы равны сумме проекций всех сил, действующих на любую из частей стержня, на оси x и y, соответственно;крутящий момент равен сумме моментов всех сил, действующих на любую из частей стержня, относительно продольной оси z;изгибающие моменты равны сумме моментов всех сил, действующих на любую из частей стержня, относительно осей x и y, соответственно.
6.Какой вид нагружения называется растяжением-сжатием
Растяжением или сжатием называют вид нагружения, при котором в поперечном сечении бруса возникает только один внутренний силовой фактор -продольная сила. Продольные силы меняются по длине бруса. При расчётах после определения величин продольных сил по сечениям строится график - эпюра продольных сил. Условно назначают знак продольной силы Если продольная сила направлена от сечения, то брус растянут. Растяжение считают положительной деформацией. Если продольная сила направлена к сечению, то брус сжат. Сжатие считают отрицательной деформацией.
|
7.Каким методом строятся эпюры внутренних силовых факторов?Применение на примере построения эпюры продольных сил
Рассмотрим брус, обладающий хотя бы одной плоскостью симметрии нагруженный произвольной системой сил (рис. 1.1,а). Свяжем с ним прямоугольную декартову систему координат. Ось zсовместим с осью бруса (геометрическое место центров тяжести поперечных сечений), а две другие, xи y , расположим в плоскости поперечного сечения, совместив одну из них, например, ось y, с осью симметрии последнего.
|
Рассечем
брус плоскостью П, перпендикулярной к
оси z,
на две части и одну из частей, например
П, отбросим, заменив ее действие на
оставшуюся внутренними силами (рис.
1.1,б). Выбрав в качестве центра приведения
центр тяжести сечения abcd,
заменим внутренние силы их интегральными
характеристиками – главным вектором ![]() и
главным моментом
и
главным моментом ![]() .
Раскладывая
и
по
осям x, y и z,
получим
.
Раскладывая
и
по
осям x, y и z,
получим  (1.1)
Здесь Nz –
продольная сила; Qx(Qy)
– поперечные силы; Mx(My)
– изгибающие моменты; Mz
крутящий момент. Это и есть внутренние
силовые факторы в поперечном сечении
бруса.
Для расчета конструкций
на прочность необходимо знать, как
изменяются внутренние силовые факторы
по длине бруса. С этой целью строятся
их графики, называемые эпюрами.
Построение
эпюр продольных сил
(1.1)
Здесь Nz –
продольная сила; Qx(Qy)
– поперечные силы; Mx(My)
– изгибающие моменты; Mz
крутящий момент. Это и есть внутренние
силовые факторы в поперечном сечении
бруса.
Для расчета конструкций
на прочность необходимо знать, как
изменяются внутренние силовые факторы
по длине бруса. С этой целью строятся
их графики, называемые эпюрами.
Построение
эпюр продольных сил ![]()
Продольная сила в сечении численно равна алгебраической сумме проекций всех сил, приложенных по одну сторону от рассматриваемого сечения, на продольную ось стержня.
Правило знаков для : условимся считать продольную силу в сечении положительной, если внешняя нагрузка, приложенная к рассматриваемой отсеченной части стержня, вызывает растяжение и отрицательной - в противном случае.
Пример 1. Построить эпюру продольных сил для жестко защемленной балки (рис.4).
Порядок расчета:
1. Намечаем характерные сечения, нумеруя их от свободного конца стержня к заделке.
2. Определяем продольную силу в каждом характерном сечении. При этом рассматриваем всегда ту отсеченную часть, в которую не попадает жесткая заделка.
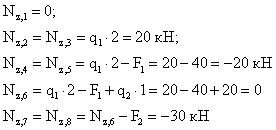
3. По найденным значениям строим эпюру .
Положительные значения откладываются (в выбранном масштабе) над осью эпюры, отрицательные - под осью.
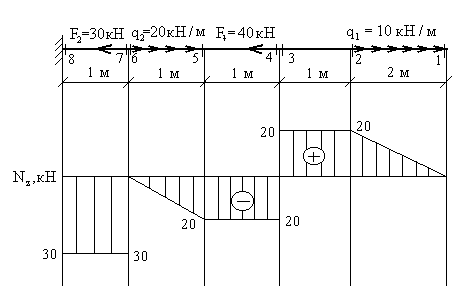

 Рис.
1.1
Рис.
1.1