5.2 Графический анализ результатов расчета

Следующим шагом будет графический анализ полученного решения. Установим курсор в позицию Графический анализ раздела Результаты дерева проектов и нажмем левую кнопку мыши. При этом активизируется окно постпроцессора, инструментальная панель которого включает различные функции отображения результатов расчета.

5.3 Анализ перемещений

Анализ перемещений выполняется с помощью функций раздела Деформации (рисунок 11). Для анализа перемещений необходимо выполнить следующие операции:

• активизировать режим анализа перемещений (закладка Деформации);

• выбрать в списке номер загружения;

• выбрать направление перемещения;

• нажать на одну из кнопок функций отображения результатов.

Рисунок 11 - Инструментальная панель режима анализа перемещений (Деформации)

5.4 Анализ напряжений

Обычно напряжения в элементах относятся к местным системам координат. У конечного элемента 22-го типа местная система координат совпадает с глобальной (общей) системой координат.

А нализ напряжений выполняется с помощью функций раздела Поля напряжений. На рисунке 12 дано отображение изополей компонента NX (_x) напряжения.

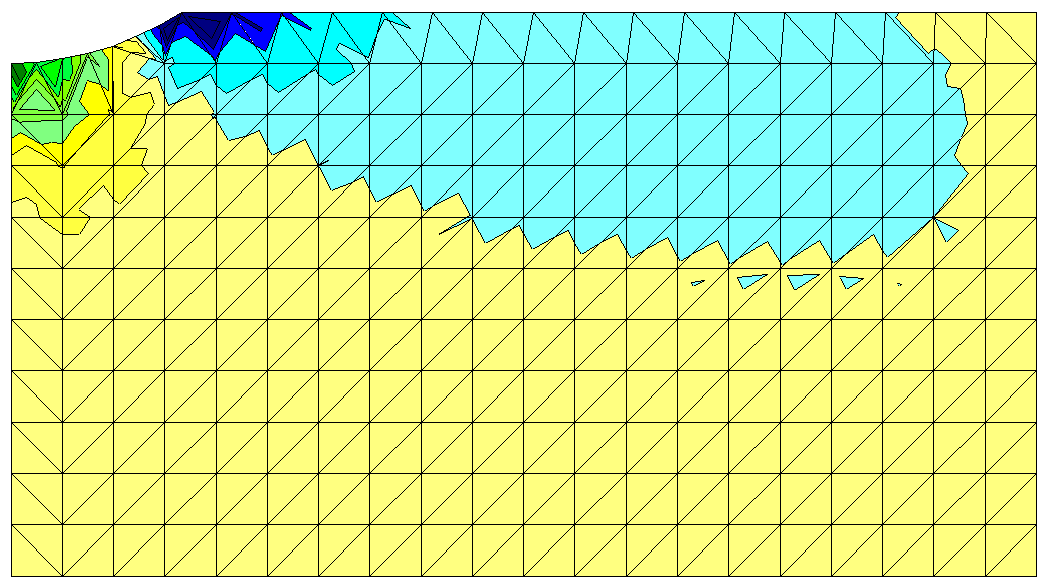
Рисунок 12 - Карта нормального компонента _x напряженного состояния

Максимальное напряжение возникает в элементе 2: σ_x=52242,7 кН/м²=52,2427МПа (рисунок 13).

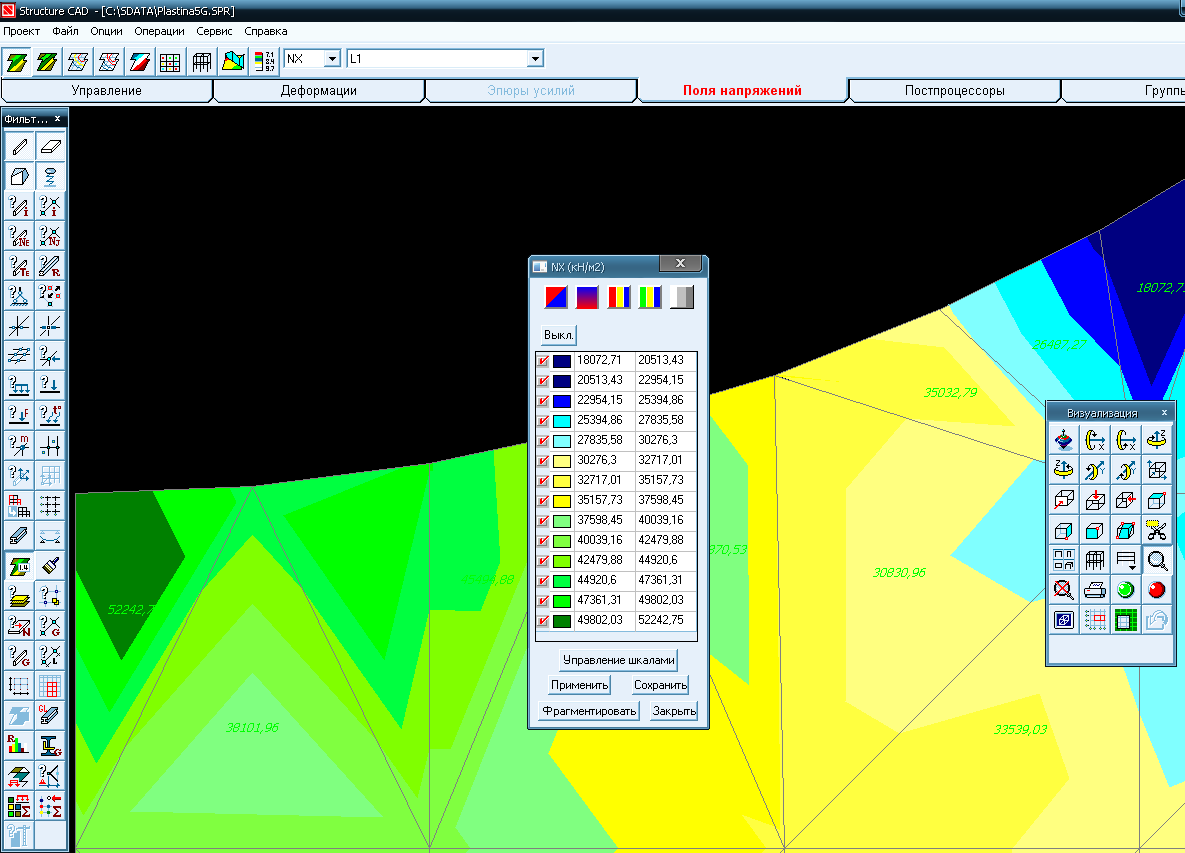
Рисунок 13 - Увеличенная карта нормального компонента _x напряженного состояния

Также можно провести контроль расчета, зайдя в раздел деформации и в инструментальной панели выбрав кнопку Анимация перемещений . Это покажет поведение пластины при действии нагрузки (рисунок 14).

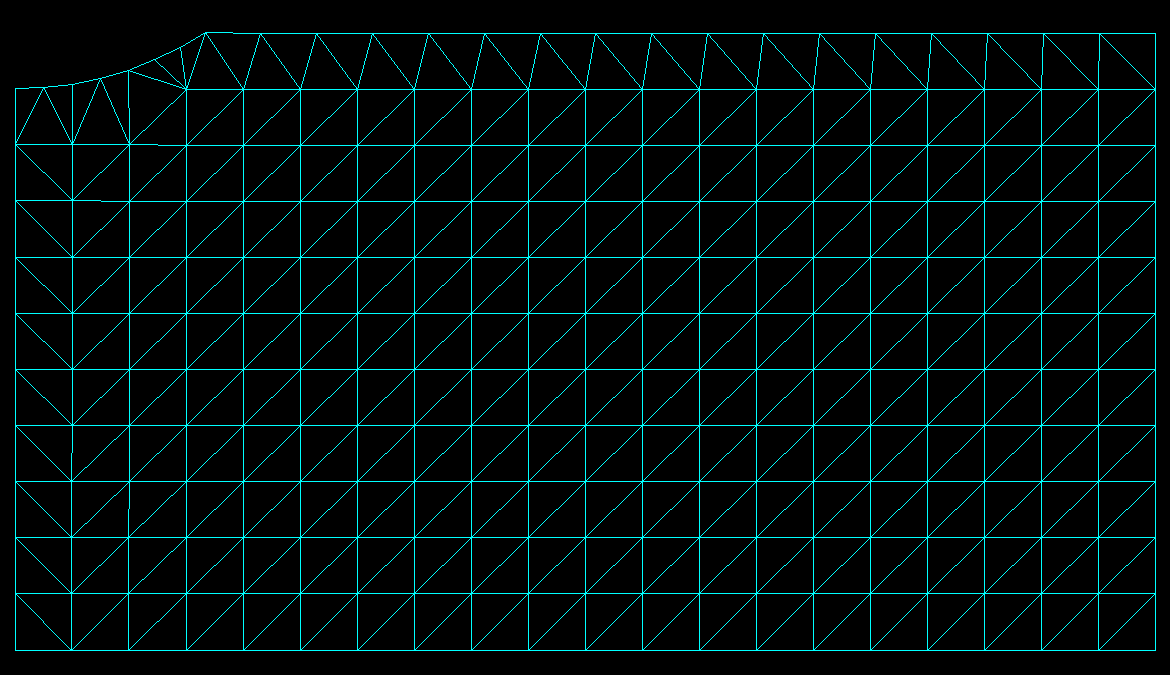
Рисунок 14 - Анимация перемещений

5.5 Печать и анализ результатов

Для того, чтобы просмотреть или распечатать результаты расчета, следует перейти в Дерево и активизировать позицию Печать таблиц раздела Результаты. В диалоговом окне Оформление результатов расчета (рисунок 14) выбираем разделы, например, Усилия и напряжения, и активизируем его.

Устанавливаем параметры выходных данных, нажимая на кнопку Параметры вывода. В появившемся окне задаем Выходные единицы измерения: перемещения – мм, усилия и напряжения – кН, единицы длины для силовых факторов – м.

Тогда напряжения будут представлены кН/м². Нажимаем ОК, Формирование документа и Просмотр результатов, вызывая тем самым текстовый редактор WordPad с таблицами результатов.

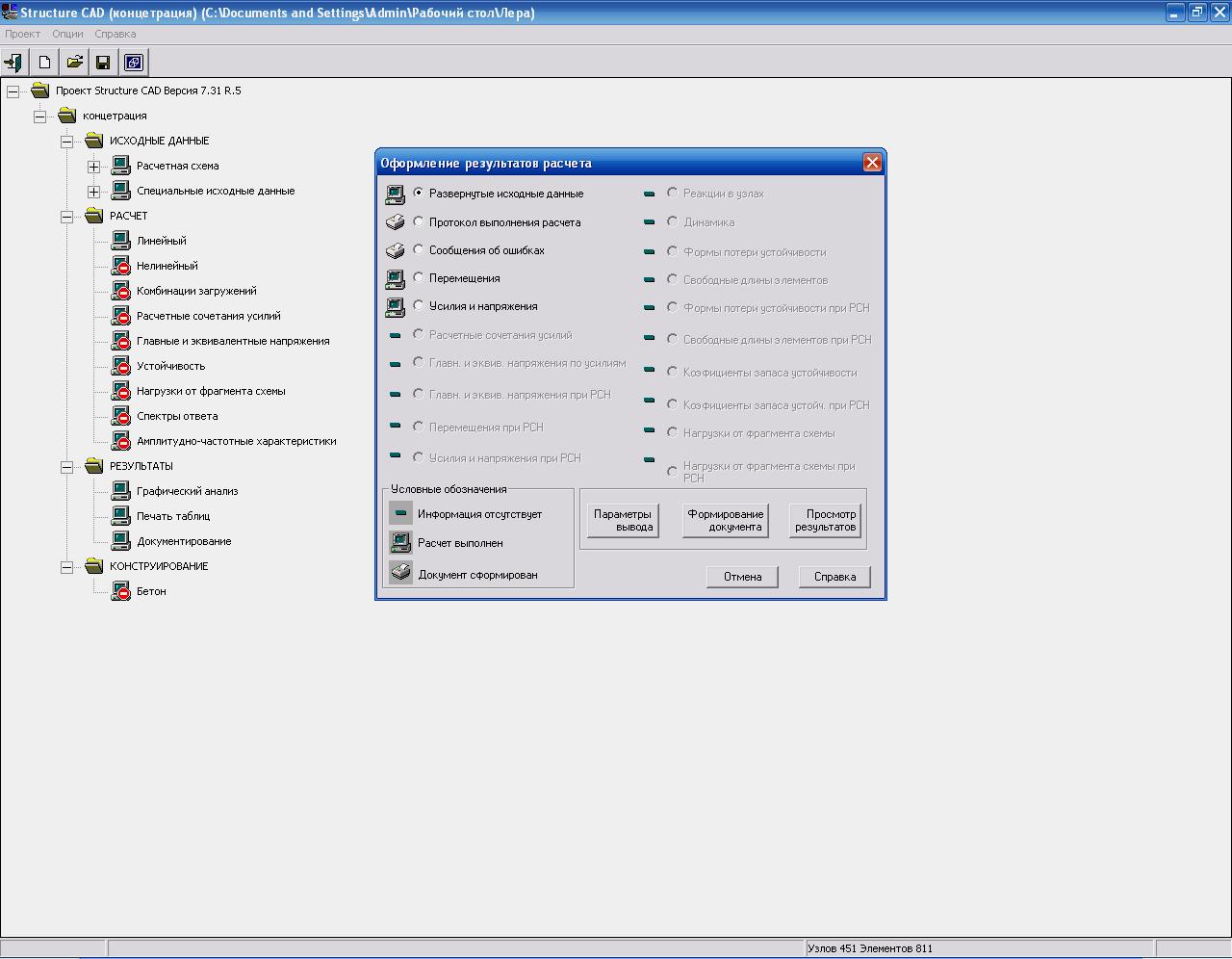
Рисунок 15 - Диалоговое окно Оформление результатов расчета

На экране появится документ с таблицами напряжений в конечных элементах. В конце документа размещается таблица "Максимальные усилия /напряжения/ в элементах расчетной схемы", из которой выписываем значение наибольшего растягивающего напряжения: σ_max=52242,7 кН/м²=52,24МПа. Оно возникает в элементе № 2.

Номинальное напряжение можно найти по формуле из сопротивления материалов:

Коэффициент концентрации напряжений в данной задаче найдем из отношения:

Отметим, что эта величина соответствует конечно-элементной схеме, состоящей из 811 элементов и имеющей 451 узлов.

В изуальная проверка полученного решения может быть сделана на основе анализа деформаций схемы. Для этого переходим в Дерево и выбираем Графический анализ, затем активизируем раздел Деформации и нажимаем кнопку Совместное отображение исходной и деформированной схемы. Анализ деформаций позволяет, в частности, проверить выполнение условий закрепления.