Министерство образования и науки Российской Федерации

Федеральное государственное бюджетное образовательное учреждение

высшего профессионального образования

«Алтайский государственный технический университет им. И.И. Ползунова»

Кафедра "Прикладная механика"

УДК 624.04 (075.8)

Курсовая работа защищена

с оценкой _______________

Руководитель : доцент,

к.т.н. ________ В.Г.Бусыгин

Исследование концентрации напряжений методом конечных элементов

Пояснительная записка к курсовой работе по дисциплине

«Вычислительная механика»

КР 150301.5Г.000ПЗ

Студент группы ДПМ-81_____________Матвиенко О.Ю.

Барнаул 2012

О главление

Исследование концентрации напряжений 1

методом конечных элементов 1

1 Постановка задачи и исходные данные 2

2 Вычисление теоретического коэффициента концентрации 5

3 Создание нового проекта в среде SCAD 6

4 Формирование расчетной схемы 8

4.1 Общие сведения 8

4.2 Ввод опорных узлов 8

4.3 Формирование контура пластинки 9

4.4 Триангуляция расчетной схемы 9

4.5 Назначение типа элементов 11

4.6 Задание жесткости пластинки 12

4.7 Назначение связей 12

4.8 Задание нагрузок 12

5 Расчет и анализ результатов 15

5.1 Расчет проекта 15

5.2 Графический анализ результатов расчета 15

5.3 Анализ перемещений 15

5.4 Анализ напряжений 15

5.5 Печать и анализ результатов 18

Список литературы 21

Приложение А 22

1 Постановка задачи и исходные данные

Целью курсовой работы является исследование методом конечных элементов напряженного состояния и определение коэффициента концентрации напряжений в плоских элементах машиностроительных конструкций. Решение МКЭ предполагается получить с помощью пакета прикладных программ SCAD. Предлагаемая для численного решения задача имеет аналитическое решение, на основе которого в работе [2 ] приведен график (рисунок 2), по которому может быть вычислен теоретический коэффициент концентрации напряжений.

Исследуем напряженное состояние пластинки, ослабленной двумя широкими симметричными выкружками по краям и растянутой торцевой нагрузкой Р (рисунок 1).

Исходные данные: толщина пластинки: h=1 см, t=0,6 см, D=13,2 см, r=3,6 см, P =40 кН, модуль упругости материала пластинки E = 2,1·10⁵ MПа, коэффициент Пуассона ν = 0,3.Выберем длину пластинки L=24см.

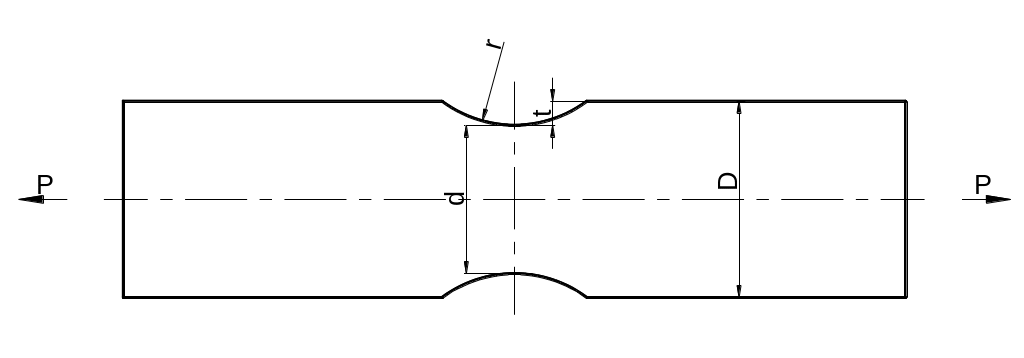
Рисунок 1 – Заданная схема пластинки

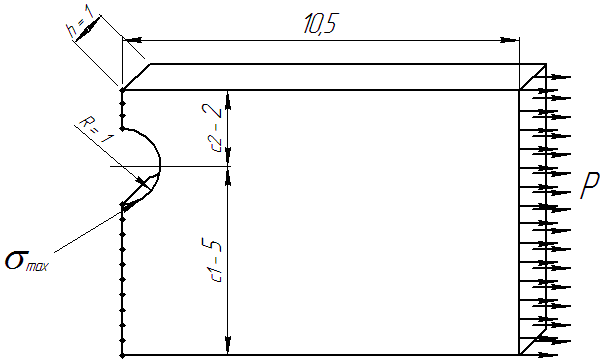
Расчет пластинки в данном случае классифицируется как плоская задача теории упругости (расчет плоского напряженного состояния). Сетка не должна быть слишком мелкой – использовано не более 1500 конечных элементов треугольной формы. В то же время сетка достаточно точно аппроксимирует имеющиеся в пластинке выкружки.

Деталь имеет вертикальную и горизонтальную ось симметрии, расчетная схема составляется из четверти схемы детали. Для бесконечной пластины назначены конечные размеры расчетной схемы на основе принципа Сен-Венана.

2 Вычисление теоретического коэффициента концентрации

Как уже сказано в главе 1, данная задача имеет теоретическое решение, полученное с помощью методов теории упругости. График, показанный на рисунке 2, позволяет узнать величину K при известных величинах r/d и D/d.

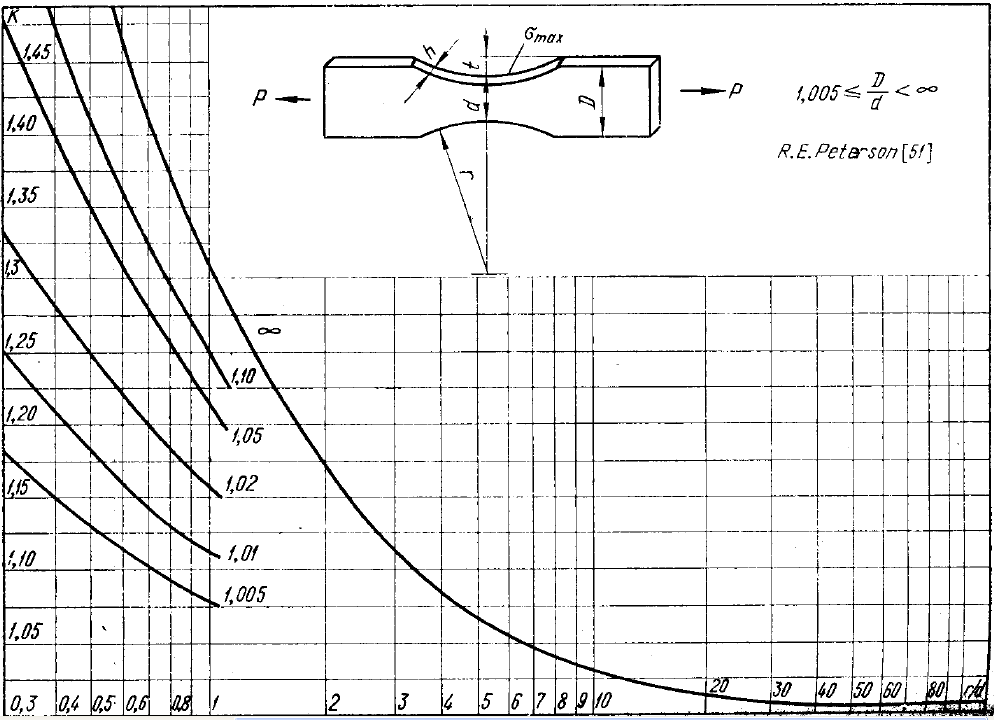
Рисунок 2 - График расчета величины коэффициента концентрации напряжений в исходной пластине

В нашем случае r/d=0,3 и D/d=1,1 получим K=1,65