7. Система масового обслуговування з відмовами

Розглянемо систему з п однаковими обслуговуючими приладами, в яку надходить найпростіший потік заявок з інтенсивністю . Тривалість обслуговування однієї заявки розподілена за показниковим законом з параметром . Заявка, що надійшла, коли всі прилади зайняті, покидає систему. Кожен прилад одночасно може обслуговувати тільки одну заявку.

Позначимо через – випадковий процес, що в кожен момент часу співпадає з числом зайнятих приладів в системі. Простір станів процесу має вигляд . Стан "0" означає, що в системі немає зайнятих приладів, стан "1" – один зайнятий прилад, а всі інші простоюють, ..., "п" – всі прилади зайняті. Граф переходів із стану в стан має вигляд, зображений на рис. 12.

Рис. 12.

Інтенсивності, що стоять на стрілках, знаходимо з допомогою теорем (1) та (2) з розділу 3.

Наприклад:

,

, .

Процес – процес загибелі та народження. Граничні ймовірності станів знаходимо, враховуючи результати розділу 5:

,

.

Останні формули називають формулами Ерланга. Заявка отримає відмову, якщо вона застане всі прилади зайнятими, тобто система знаходиться в стані "п", це означає, що ймовірність відмови співпадає з :

.

Позначимо через відносну пропускну здатність системи:

,

тоді абсолютна пропускна здатність (позначимо її через А) обчислюється за формулою

.

Позначимо через середнє число зайнятих приладів:

.

Можна показати, що

.

Приклад. СМО з відмовами представляє собою три телефонні лінії. Заявка, що надійшла в момент, коли всі лінії зайняті, отримує відмову. Інтенсивність потоку заявок (заявок за хвилину). Середня тривалість розмови хвилини. Всі потоки подій – найпростіші. Визначити граничні (при ) значення ймовірностей станів, ймовірності відмови та середнього числа зайнятих каналів, абсолютну та відносну пропускну здатності.

Розв’язування. Обчислимо , , а пов’язане з середнім часом обслуговування обернено пропорційною залежністю:

.

Тоді .

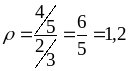За формулами Ерланга одержуємо:

,

,

,

.

Тоді

; ; .

Ймовірність відмови

.

Відносна та абсолютна пропускні здатність дорівнюють:

.

Середнє число зайнятих каналів

,

тобто в усталеному режимі роботи СМО в середньому буде зайнятий один з невеликим канал з трьох – інші два будуть простоювати. Цією ціною досягається порівняно високий рівень ефективності обслуговування – близько 91 % всіх заявок, що надходять в систему, будуть обслужені.

Коли число обслуговуючих каналів велике, розрахунки за формулами Ерланга стають громіздкими, тому в цьому випадку краще характеристики системи обчислювати на ЕОМ. При програмуванні формул Ерланга треба зважати на те, що вираз , якщо його обчислення програмувати безпосередньо так, як записаний вираз, призводить до виникнення помилки "переповнення". Щоб уникнути цієї помилки, треба цей вираз програмувати у циклі, як добуток:

.

8. Система масового обслуговування з обмеженою чергою

В систему надходить найпростіший потік заявок з інтенсивністю . Число обслуговуючих приладів дорівнює п. Є т місць дожидання. Коли заявка, що надійшла в систему, застає хоча б один вільний прилад, вона негайно береться на обслуговування. Якщо ж всі прилади зайняті, але є хоч одне вільне місце дожидання, то заявка стає в чергу і дожидається, поки звільниться хоча б один прилад. Якщо ж і всі прилади зайняті і всі місця дожидання зайняті, то заявка отримує відмову і покидає систему необслуженою. Кожен прилад обслуговує одночасно тільки одну заявку. Час обслуговування – випадкова величина, що розподілена за показниковим законом з параметром . Тобто середній час обслуговування однієї заявки дорівнює  .

Позначимо через – число заявок в системі в момент часу (на обслуговуванні та в черзі). Простір станів має вигляд

.

Граф переходів із стану в стан має вигляд (рис. 13)

0 1 2 . . . . . .

Рис. 13.

– процес загибелі та народження. Граничні ймовірності станів в усталеному режимі мають вигляд:

,

,

.

Середнє число зайнятих приладів ,

ймовірність відмови ,

відносна пропускна здатність ,

абсолютна пропускна здатність ,

середня довжина черги ,

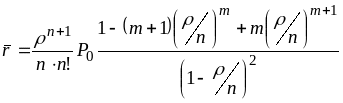середнє число заявок в системі ,

середній час дожидання початку обслуговування ,

середній час перебування заявки в системі .

Приклад. Біля поста ДАІ три автоінспектори перевіряють путьові листи у водіїв вантажних автомобілів. На перевірку путьового листа інспектор затрачує в середньому 5 хвилин. Потік вантажних машин найпростіший, його інтенсивність дорівнює одному автомобілю за хвилину. Інспектори підрахували, що оскільки в середньому кожну хвилину під’їжджає новий автомобіль, а перевірити вони можуть в середньому не більше путьових листів, то дуже скоро біля пункту ДАІ виросте довгий хвіст машин і рух застопориться. Тому інспектори вирішили, що черга не повинна перевищувати трьох машин. Якщо автомобіль, що проїжджає, застає в черзі три машини, то його не зупиняють. Знайти середню довжину черги з машин, що стоять біля пункту ДАІ та ймовірність того, що вантажний автомобіль, що проїздить біля пункту ДАІ, не буде зупинено.

Розв’язування. Пункт ДАІ представляє собою систему масового обслуговування з обмеженою чергою. В ролі обслуговуючих приладів виступають автоінспектори, тобто . Число місць дожидання за умовою задачі . Інтенсивність вхідного потоку , інтенсивність обслуговування , .

Обчислимо середню довжину черги

.

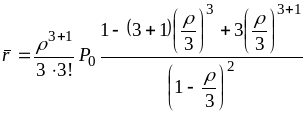Знайдемо спочатку :

.

Тепер

.

Ймовірність того, що вантажний автомобіль, який проїздить біля пункту ДАІ, не буде зупинено, дорівнює

.