5. Процес загибелі та народження

Процес, про який піде мова далі, широко використовується в математичних моделях масового обслуговування та надійності.

Марковський процес з множиною станів називають процесом загибелі та народження, якщо граф його станів має вигляд, представлений на рис.10.

0 1 2 . . . . . .

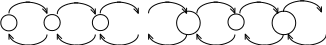
Рис. 10.

Доведено, що для процесів загибелі та народження існують граничні ймовірності

,

які мають вигляд: ,

де ,

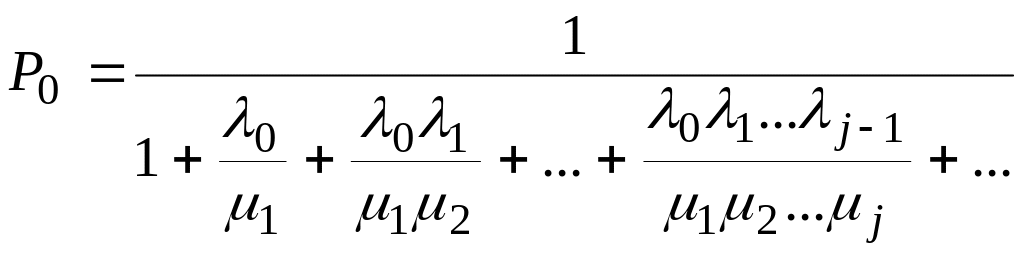якщо сума ряду, що стоїть в знаменнику , скінчена. Якщо ж ряд розбіжний, то і всі . В останньому випадку, в системі, що описується таким процесом, усталений режим не існує, процес при прямує до .

П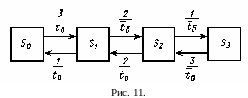 риклад. Прилад складається з трьох вузлів; потік відмов – пуассонівський процес, середній час безвідмовної роботи кожного вузла дорівнює , вузол, що відмовив, зразу ж починає ремонтуватись; середній час ремонту (відновлення) вузла дорівнює , закон розподілу цього часу показниковий (потік відновлень – пуассонівський процес). Знайти середню продуктивність приладу, якщо при трьох працюючих вузлах вона дорівнює 100 %, при двох – 50 %, а при одному і менше – прилад взагалі не працює.

Розв’язування. Перерахуємо можливі стани нашої системи:

– всі три вузли справні;

– один вузол відмовив (відновлюється), два справні;

– два вузли відновлюються, один справний;

– всі три вузли відновлюються.

Граф станів має вигляд, що показаний на рис. 11.

Інтенсивності переходів, що проставлені на стрілках, знайдено з використанням теорем 1-2 (розділ 3). За умовою задачі час безвідмовної роботи одного вузла розподілений за показниковим законом, середній час безвідмовної роботи , тому параметр розподілу . Інтенсивність переходу з в знаходимо за теоремою 2, враховуючи, що ймовірність того, що з трьох вузлів за час з ладу вийде один вузол, обчислюється за біномним законом:

.

Аналогічно

,

.

Інтенсивності переходів з в , з в , з в знаходяться аналогічно, тільки параметр показникового закону .

Процес, що описує роботу системи, є процесом загибелі та народження. Використовуючи вираз для граничних ймовірностей станів цього процесу, одержимо

;

;

;

.

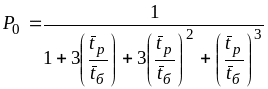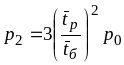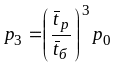Середня продуктивність приладу в усталеному режимі

.

6. Поняття системи масового обслуговування. Типи систем масового обслуговування та їх характеристики

Під системою масового обслуговування (СМО) розуміють математичну модель, що складається з таких елементів:

1. вхідний потік заявок (вимог);

2. обслуговуючі прилади (канали);

3. дисципліна обслуговування;

4. вихідний потік заявок.

Кожна СМО призначена для обслуговування деякого потоку заявок, що надходять в СМО в якісь, взагалі кажучи, випадкові моменти часу. Обслуговування заявки, що надійшла, триває деякий, взагалі кажучи, випадковий час, після чого прилад звільнюється і готовий до прийняття наступної заявки.

В ролі заявок можуть бути люди, пароплави, поїзди, літаки і т.д. В ролі обслуговуючих приладів можуть виступати сортувальна гірка на станції, люди, станки, білетні каси і т.д.

Випадковий характер потоку заявок призводить до того, що в деякі проміжки часу на вході СМО накопичується занадто велике число заявок (вони або утворюють чергу або покидають систему необслуженими); в інші періоди СМО буде працювати з недовантаженням або взагалі простоювати.

Кожна система масового обслуговування, в залежності від числа каналів і їх продуктивності, а також від характеру потоку заявок, має якусь пропускну здатність, що дозволяє їй більш-менш успішно справлятись з потоком заявок.

Предмет теорії масового обслуговування – встановлення залежності між характером потоку заявок, числом каналів, їх продуктивністю, правилами роботи СМО і успішністю (ефективністю) обслуговування.

СМО можна розподілити на системи без черг і системи з чергою. Якщо в системі не буває черги, то можливі два варіанти. Перший – система з відмовами – заявка, заставши всі прилади зайнятими, покидає систему необслуженою. Коли ви, набравши потрібний номер телефону, чуєте короткі гудки, це значить, що на АТС всі лінії зв’язку зайняті. Ви отримали відмову. Другий варіант – система без відмов – з необмеженим числом приладів. В житті таких систем, звичайно, не буває, однак, коли число приладів набагато більше можливого числа заявок, зручно вважати число приладів нескінченним. Прикладом може служити та ж АТС в нічний час. Потік телефонних викликів вночі невеликий, і на АТС завжди знайдеться вільна лінія для вашої розмови.

Системи з чергою, або з дожиданням, теж можна розбити на дві групи: системи з необмеженою чергою і системи з обмеженою чергою. В першому випадку заявка, що попала в систему, не вийде з неї необслуженою незалежно від того, в якому стані вона застала систему і скільки їй прийдеться стояти в черзі. Наприклад, на вантажній станції всі вагони будуть стояти в черзі, поки їх не розвантажать. Прикладом системи з обмеженою довжиною черги може бути управляюча обчислювальна машина, в яку надходять повідомлення про стан деякого об’єкта. Оскільки буферний запам’ятовуючий пристрій має обмежену ємність, у випадку відсутності в ньому вільних ячейок нові повідомлення, що надходять, губляться.

Дисципліна обслуговування – це порядок, у якому заявки з черги надходять на обслуговування. В тих чергах, з якими ми щоденно маємо справу, заявки звичайно обслуговуються в порядку надходження. Однак може бути і інший порядок – наприклад, інверсійний – заявки обслуговуються в порядку, оберненому порядку надходження, або випадковий – заявки вибираються з черги випадково. Крім того, важливий клас складають системи, в які поступають заявки з різними пріоритетами. В таких системах заявки з більш високим пріоритетом обслуговуються в першу чергу. Так, на телеграфі в першу чергу посилають термінові телеграми, літаки, що йдуть на посадку, мають перевагу перед літаками, що готуються злітати.

СМО розрізняються і за структурою обслуговуючого пристрою. Бувають системи одноканальні – з одним приладом і багатоканальні – з декількома приладами. Про теоретичний випадок нескінченного числа приладів говорилось раніше.

Розглянемо вхідний потік заявок. Інтервали, через які заявки надходять до системи, – випадкові величини (в окремому випадку вони можуть бути постійні: заявки надходять через рівні інтервали, утворюючи регулярний потік). Різні види розподілів довжин цих інтервалів і кількості заявок, що одночасно надходять до системи, породжують різні вхідні потоки.

Ми в подальшому будемо користуватись так званим найпростішим вхідним потоком. Вхідний потік, процес надходження заявок в якому описується пуассонівським процесом, називають найпростішим. Цей потік заявок має наступні властивості:

1. ймовірність надходження певної кількості заявок за деякий проміжок часу залежить тільки від довжини цього проміжку і не залежить від того, де на осі часу знаходиться цей проміжок. Цю властивість називають стаціонарністю потоку. В природі стаціонарних потоків не існує, але дуже багато з них можна без особливої похибки вважати стаціонарними, або такими, що мають стаціонарні ділянки. Потік пасажирів, що бажають придбати квиток на поїзд далекого прямування вдень і вночі не один і той же (каси працюють цілодобово). Однак між 10-ю та 14-ю годинами цей потік, як правило, можна вважати стаціонарним. Стаціонарний потік має постійну інтенсивність надходжень (інтенсивність – це математичне сподівання числа заявок, що надходять за одиницю часу);

2. найпростіший потік заявок є ординарним. Потік називається ординарним, якщо в будь-який момент часу може надійти тільки одна заявка;

3. найпростіший потік має ще одну чудову властивість, що називається відсутністю післядії. Вона полягає в тому, що час, що залишився до моменту надходження нової заявки, не залежить від того, скільки часу пройшло після надходження останньої заявки. Функція розподілу інтервалів між заявками цього потоку

,

де називається параметром потоку, а число заявок, що надходять за проміжок часу , розподілене за законом Пуассона

,

де – ймовірність того, що за проміжок часу надійде рівно заявок, .

В залежності від типу СМО при оцінюванні її ефективності застосовують ті чи інші величини (показники ефективності). Наприклад, для СМО з відмовами однією з найважливіших характеристик її продуктивності є так звана абсолютна пропускна здатність – середнє число заявок, що може обслужити система за одиницю часу. Нарівні з абсолютною часто розглядається відносна пропускна здатність СМО – відношення середнього числа заявок, що обслуговуються системою в одиницю часу, до середнього числа заявок, що надійшли за цей час.

Окрім абсолютної та відносної пропускної здатностей, при аналізі СМО з відмовами нас можуть, в залежності від задачі дослідження, цікавити і інші характеристики, наприклад:

• середнє число зайнятих каналів,

• середній відносний час простоювання системи в цілому і окремого канала і т.д.

Для системи з необмеженим дожиданням як абсолютна, так і відносна пропускна здатність втрачають смисл, оскільки кожна заявка, що надійшла, рано чи пізно буде обслужена. Для таких СМО досить важливими характеристиками є:

• середнє число заявок в черзі,

• середнє число заявок в системі (в черзі і на обслуговуванні),

• середній час дожидання заявки в черзі,

• середній час перебування заявки в системі (в черзі і на обслуговуванні)

та інші характеристики.

Математичний аналіз роботи СМО дуже полегшується, якщо випадковий процес, що протікає в системі, марковський. Надалі будемо розглядати саме такі системи.