Процеси з незалежними приростами

Якщо випадкові величини

незалежні для всіх таких, що

, ,

то процес є процесом з незалежними приростами.

Прикладом такого процесу може бути так званий пуассонівській процес: процес з простором станів називають пуассонівським, якщо виконуються умови:

1. у початковий момент часу процес знаходиться в стані "0"

;

2. – процес з незалежними приростами;

3. прирости процесу розподілені згідно з законом Пуассона:

,

.

Пуассонівський процес є хорошою математичною моделлю для багатьох транспортних потоків, для потоків заявок на телефонні станції. Якщо ми маємо справу з якою-небудь складною радіотехнічною системою, що складається з великого числа елементів, кожний з яких з малою ймовірністю може відмовити в роботі за одиницю часу незалежно від інших елементів, то число елементів, що відмовили за проміжок часу , становить випадковий процес, який в багатьох випадках добре описується пуассонівським процесом. Пуассонівський процес з великою точністю описує численні природничо-наукові явища і технічні процеси.

Стаціонарні процеси

Випадковий процес називають стаціонарним у вузькому смислі слова, якщо сумісні розподіли сімейств випадкових величин

та

співпадають для всіх і з , .

Випадковий процес називають стаціонарним в широкому смислі, якщо

1. ,

2. .

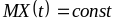Це означає, що кореляційна функція не залежить від того, де і лежать на осі часу, а залежить тільки від відстані між ними.

Рис. 4.

Рис. 5.

На рисунку 4 зображено стаціонарний в широкому смислі процес, на рисунку 5 – нестаціонарний.

Марковські процеси (процеси без післядії)

Марковський процес – це процес, який має властивість: коли відоме значення випадкової величини , то ймовірність значення , , не залежить від , , тобто ймовірнісні характеристики поведінки процесу в "майбутньому" не залежать від того, в яких станах і як довго процес перебував в "минулому", а залежать тільки від того, в якому стані процес перебуває зараз, в теперішній момент часу.

Розглянемо приклад. Нехай система представляє собою технічний пристрій, який вже проробив деякий час, відповідним чином "зносився" і прийшов у деякий стан, що характеризується повним ступенем зношеності . Нас цікавить, як буде працювати система в майбутньому. Ясно що, принаймні в першому наближенні, характеристики роботи системи в майбутньому (частота відмов, необхідність ремонту) залежать від стану пристрою в теперішній момент і не залежать від того, коли і як пристрій досяг свого теперішнього стану.

Теорія марковських випадкових процесів має широкий спектр різноманітних застосувань – від опису фізичних явищ типу дифузії або премішування шихти під час плавки в доменній печі до процесів утворення черг або розповсюдження мутацій генів в біологічній популяції.

Процеси з незалежними приростами є окремим частковим випадком марковських процесів.

Марковські процеси широко використовуються в теорії масового обслуговування та надійності.