38.Кривые поверхности. (Определение; способы задания; касательные и нормали к поверхности; особые точки поверхности; кривизна поверхности).

Для завдання поверхні застосовують різні способи, з яких основними є наступні:

1) Аналітичний спосіб – поверхню розглядають як геометричне місце крапок, координати яких задовольняють заданому рівнянню (алгебраїчні й трансцесдентні поверхні).

2) Кінематичний спосіб – поверхні утворяться безперервним переміщенням у просторі лінії (утворюючої) за певним законом.

3) Каркасний спосіб – поверхні задають деяким числом (сукупністю) лежачих на них ліній – каркасом.

Динамічними називаються поверхні складних технічних форм, що обмежують деталі, вузли, агрегати або вироби, взаємодіючі із середовищем, і у зв'язку із цим, що відповідають певним наперед заданим технічним умовам.

Зовнішніми динамічними називаються поверхні, обтичні середовищем.

Внутрішніми динамічними називаються поверхні, що направляють середовище.

Основною функціональною загальною характеристикою зовнішніх і внутрішніх динамічних поверхонь, є мінімум гідравлічних втрат у прикордонному шарі потоку й потоці в цілому. Поряд із цим до функціональних характеристик зовнішніх динамічних поверхонь можна віднести регламентовану піднімальну силу (крило), поворот потоку або струменя (рули), мінімальний лобовий опір і ін.; для внутрішніх динамічних поверхонь це транспортування середовища, підвищення (дифузор) або зниження (конфузор) тиску в потоці, поворот потоку та ін.

2. Локальні характеристики поверхонь

2. А) Дотична пряма поверхні

Поняття дотичній прямій до поверхні засновано на уведеному раніше визначенні дотичної до плоскої й просторової кривої.

Граничне положення прямої, що перетинає поверхню у двох крапках, коли точки перетинання збігаються, представляє дотичну до поверхні. Через крапку поверхні проходить незліченна безліч кривих qⁱ, кожна з яких має в крапці М свою дотичну. По визначенню, кожна із цих дотичних, буде в той же час дотичної до поверхні. Звідси випливає, що через точку поверхні проходить безліч дотичних.

Дотична площина поверхні в даній точці містить дотичні, побудовані до кожної з кривих ліній, намічених на поверхні і що проходять через дану точку. Звідси випливає, що дотичну площину в даній точці поверхні можна визначити як площина, утворена дотичними до двох будь-яких ліній, побудованим на поверхні та пересічної в заданій на поверхні точці.

Дотичні площини можна побудувати не у всякій точці поверхні. Залежно від цього, точки поверхні поділяють на звичайні та особливі. У звичайних точках є, або може бути, побудована тільки одна певна дотична площина. В особливих точках дотична площина або не визначена, або ж існує, не будучи єдиної.

В якості прикладів особливих точок поверхонь служать:

а) вершина будь-якої конічної поверхні;

б) будь-яка точка на ребрі повернення торсової поверхні.

Пряму лінію, що проходить через точку торкання та перпендикулярну дотичної площини, називають нормаллю поверхні в даній точці. Нормаль у даній крапці поверхні визначає, отже, напрямок дотичної площини до поверхні в цій крапці.

2. в) Кривина поверхні

Подання про викривленості поверхні в наміченій на ній точці, можна одержати шляхом дослідження кривизн у цій точці кривих ліній, отриманих від перетинання поверхні рядом нормальних площин.

Площини нормальних перетинів утворять пучок площин, що має віссю нормаль поверхні в розглянутій точці, і перетинають дотичну в цій точці площина до поверхні по прямих лініях дотичним до кривих ліній нормальних перетинів.

Якщо відкладати від розглянутої точці, двусторонне, у дотичної площини, у напрямку дотичних до кривих ліній нормальних перетинів відрізки, рівні квадратним корінням з величин відповідних радіусів кривизни, то кінці цих відрізків намітять криву лінію яку називають індикатрисою Дюпена.

Для еліптичних точок індикатриса Дюпена еліпс, для гіперболічних точок - сполучена гіпербола, для параболічних точок - дві паралельні прямі лінії.

В індикатрисі Дюпена є два головних напрямки, що збігаються з її осями, для яких величини, зворотні радіусам кривизни, досягають крайніх значень. Відповідним цим кривизнам радіуси називають головними радіусами кривизни.

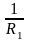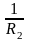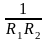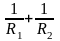Величини та , зворотні головним радіусам кривизни R₁ і R₂, називають головними кривизнами поверхні в розглянутій її точці. Добуток головних кривизн називають головною або гауссовой кривизною в даній точці, а суму – середньою кривизною поверхні в даній її точці. Радіуси кривизни мають знак, залежно від того, по яку сторону від дотичної площини розташовується відповідний центр кривизни. У гіперболічних крапках поверхонь головні радіуси кривизни мають різні знаки і тому для цих точок гауссова кривизна є негативною.