2. Исходные данные для проектирования корпуса плуга.

Робоча поверхня культурного або напівгвинтового типу для плужних корпусів будується за єдиною методикою, що полягає в побудові поверхні горизонтального цилиндроида із соответствующе обраними параметрами, та у наступному побудові робочої поверхні по її контурі в поперечно-вертикальній площині проекцій.

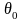Вихідними даними при проектуванні таких поверхневий є: розміри перетину шару; кут нахилу лемеша до дна борозни і кут нахилу леза лемеша (початкова утворююча) до стінки борозни; закон зміни кутів утворюючих по висоті поверхні, т, е, .

Розміри перетину шару b і а визначають контур робочої поверхні корпуса в поперечно-вертикальній площині. По заданим b і а будують лобовий контур поверхні, т, е. її поперечно-вертикальну проекцію.

Кути й (рис. 3.1) визначають початковий елементарний клин робочої поверхні, що підрізає шар.

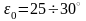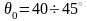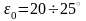Для культурних поверхонь приймають і , для напівгвинтових і .

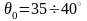3. Кривые линии, используемые при формообразовании деталей планетарно-роторных машин. (Циклоидальные кривые, трохоидные кривые, схема образования, аналитическое представление, свойства).

Конструкція більшості механізмів і машин передбачає наявність елементів, що роблять рух відносно один одного, перебуваючи в постійному контакті.

Це газорозподільний і кривошипно-шатунний механізми двигуна внутрішнього згоряння, шестерні механізми, усілякі кінематичні передачі, ін.

При конструюванні таких механізмів, однієї із ключових завдань є визначення траєкторій руху складових деталей.

Якщо крива або плоска фігура переміщюється у своїй же площині за певним законом, то траєкторією крапки, незмінно з нею зв'язаної, є деяка крива лінія. Таку криву можна визначити, як траєкторію крапки, незмінно пов'язаної з деякою рухливою кривою лінією, що котиться без ковзання по іншої нерухомої кривої лінії.

Якщо кожний з миттєвих центрів обертання незмінно зв'язати із плоскою фігурою, що рухається, то їхнім геометричним місцем є деяка крива лінія, незмінно пов'язана з фігурою. Таку криву лінію називають рухливий центроидой руху фігури.

Кривая лінія, по якій котиться без ковзання інша лінія (рухлива центроида) є геометричним місцем миттєвих центрів обертання останньої. Таку криву лінію називають нерухомою центроидой руху фігури.

У такий спосіб траєкторією крапки, незмінно пов'язаної із плоскою фігурою, що рухається, є крива лінія, яку можна розглядати як траєкторію крапки, незмінно пов'язаної з рухливий центроидой, що обкатує без ковзання нерухому центроиду. Рухлива центроида може стикатися з нерухомої, як із внутрішньої, так і із зовнішньої її сторони.

Криві лінії, побудовані за допомогою центроид, називають рулеттами. Рулетту можна задати рухливий і нерухомої центроидами та виробляючою крапкою.

Рулетту називають циклічною або циклоїдальної, якщо центроидами її є дуги окружностей.

Циклоїдальні криві застосовують при багатьох технічних розрахунках. Профілі зубів шестірень, обрис багатьох типів ексцентриків, кулачків і інших деталей машин мають форму цих кривих ліній. Циклоїдальні криві мають таке ж значення, як еліпс, парабола, гіпербола, балістична траєкторія та ін.

Розглянемо криву лінію, як траєкторію крапки окружності, що котиться без ковзання по прямої лінії. Таку криву називають циклоїдою. Пряму лінію, (нерухому центроиду) розглядаємо, як дугу окружності нескінченно великого радіуса.

Циклічну рулетту називають епіциклоідою (надциклоїдою), якщо рухлива центроида перебуває поза нерухомим центроїдом. Якщо рухлива центроїда (окружність) перебуває усередині нерухомої центроїди, то рулетту називають гіпоциклоідою (підциклоідою). Побудова епіциклоіди і гіпоциклоіди аналогічно побудові циклоїди.

Циклоїди (епіциклоіди, гіпоциклоіди) бувають подовжені і укорочені. Якщо виробляюча крапка перебуває поза виробляючим колом (рухливий центроїд), що котиться без ковзання по напрямній прямій або окружності (нерухомої центроїди), то траєкторією її є крива лінія — подовжена циклоїда (эпициклоїда, гипоциклоїда).

Якщо виробляюча точка перебуває усередині виробляючого кола, то вона при русі без ковзання кола по прямій (окружності) описує криву лінію, що називають укороченою циклоїдою (епіциклоідою, гіпоциклоідою). Подовжені й укорочені циклоїди називають інакше трохоидами.

Геометричним місцем цих точок є крива лінія – рулетта, називана эвольвентой або розгорненням кола (окружності).

Эвольвента набутила широкого застосування при конструюванні різний виробів (профіль зубів шестірень, шліців, роторів газодувок, кулачків, ін.) і моделюванні траєкторій (обводи другого порядку гладкості).