5 Выбор материала открытой конической зубчатой передачи. Определение допускаемых напряжений

5.1 Выбор материала зубчатой пары (шестерни и колеса)

Для изготовления зубчатой пары выбираем сталь 40Х [1]. Определяем ее механические характеристики [1]: предел прочности σ_в = 900 Н/мм²; предел текучести σ_т = 750 Н/мм²; предел выносливости при симметричном цикле σ_–1 = 410 Н/мм²; заготовка зубчатой пары D_пред = 125 мм, S_пред=80 мм. Применим термообработку – улучшение с твердостью для шестерни Н = 300НВ, для колеса Н=270НВ.

5.2 Определение допускаемых контактных и изгибных напряжений для зубьев шестерни и колеса

5.2.1 Определяем допускаемое контактное напряжение [σ]_H (Н/мм²) для зубьев шестерни колеса, [1]:

Н/мм²,

где

5.2.2 Определяем допускаемое напряжение изгиба [σ]_F (Н/мм²), [1]:

где К_FL – коэффициент долговечности при расчете на изгиб,

,

где N – число циклов перемены напряжений за весь срок службы, [1],

Для реверсивных передач уменьшают на 25 %

Н/мм².

6 Расчет открытой конической зубчатой передачи

Проектный расчет

6.1 Определяем главный параметр – внешний делительный диаметр колеса d_e2 (мм), [1]:

,

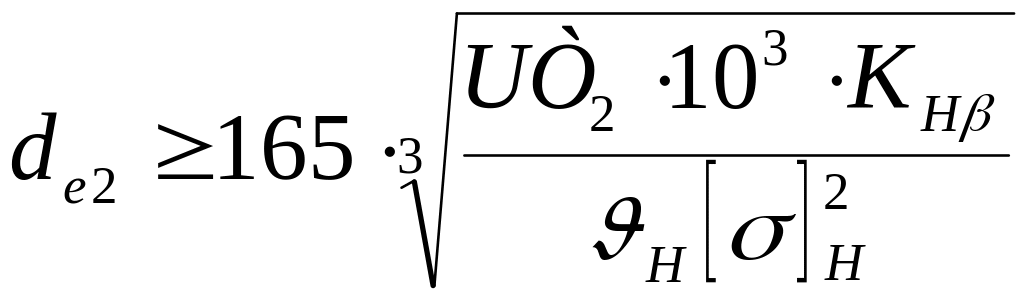где К_Hβ – коэффициент, учитывающий распределение нагрузки по ширине венца. Для прирабатывающих колес с прямыми зубьями К_Нβ=1.

ϑ_Н – коэффициент вида конических колес. Для прямозубых колес ϑ_Н=1.[1].

мм.

Полученное значение делительного диаметра колеса для нестандартных передач округляем до ближайшего числа по табл. 13.15, получаем:

d_e2=230мм.

6.2Определяем углы делительных конусов шестерни δ₁ и колеса δ₂, [1]:

.

6.3 Определяем внешнее конусное расстояние R_e:

,

6.4 Определяем ширину зубчатого венца шестерни и колеса b (мм), [1]:

мм,

b=63мм.

-коэффициент ширины венца.

6.5 Определяем внешний окружной модуль m_e– для прямозубых колес , [1]:

В силовых конических передачах m_e>1,5, при этом в открытых передачах значение модуля увеличиваем на 30% из-за повышения изнашивания зубьев

m_e=1,95.

К_Fβ – коэффициент, учитывающий распределение нагрузки по ширине венца. Для прирабатывающих колес с прямыми зубьями К_Hβ=1.

Θ_F – коэффициент вида конических колес. Для прямозубых колес ϑ_F=0,85

6.6 определяем число зубьев колеса z₂ и шестерни z₁, [1]:

.

6.7 Определяем фактическое передаточное число U_ф и проверяем его отклонение ∆U от заданного U, [1]:

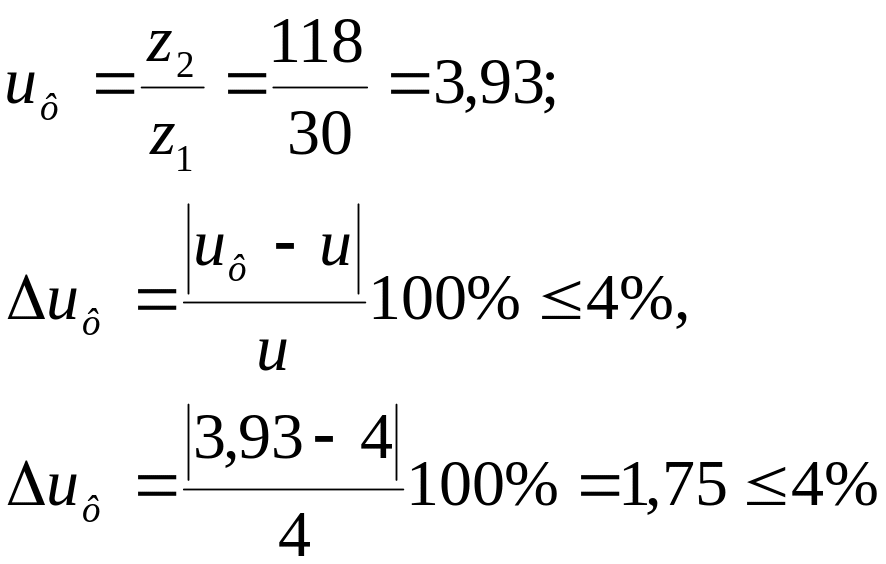
6.8 Определяем действительные углы делительных конусов шестерни δ₁ и колеса δ₂, [1]:

6.9 Для конических передач с разностью средних твердостей шестерни и колеса НВ_1ср–НВ_2ср<100 выбрать из табл. 4.6 коэффициент смещения инструмента х_е1 для прямозубой шестерни. Коэффициенты колес соответственно х_е2= – х_е1, [1].

Х_е1=0,33

6.10 Определяем фактические внешние диаметры шестерни и колеса (мм), [1].

Делительный:

мм;

Вершин зубьев:

мм.

Вершин зубьев:

,

6.11 Определяем средний делительный диаметр шестерни d₁ и колеса d₂, (мм), [1].

;

Проверочный расчет

6.12 Проверяем пригодность заготовок колес. [1]

Условие пригодности заготовок колес:

Диаметр заготовки шестерни мм,

Толщину диска или обвода колеса принимают меньшей из двух:

,

6.13 Проверяем контактные напряжения S_H, Н/мм,[1]:

с^-1;

[U] – допускаемое число ударов,

;

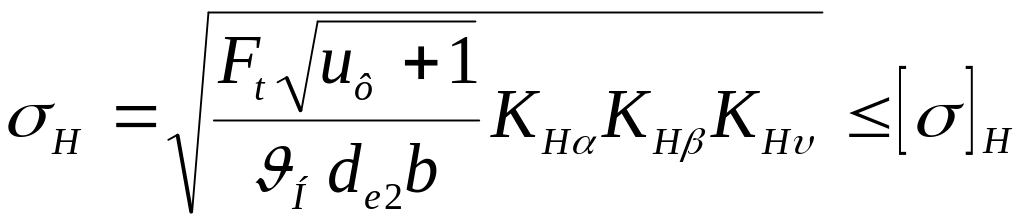Где – окружная сила в зацеплении, Н;

K_Hα=1 – коэффициент, учитывающий распределение нагрузки мезду зубьями прямозубых колес;

К_Нυ – коэффициент динамической нагрузки. Определяется по табл. 4.3 в зависимости от окружной скорости колес и степени точности передачи 9 (по табл. 4.2).

ω₂ – угловая скорость вала колеса редуктора или открытой передачи, 1/с.

К_Нυ=1,05

6.14 Проверяем напряжения изгиба зубьев шестерни σ_F1 и колеса σ_F2,Н/мм², [1]:

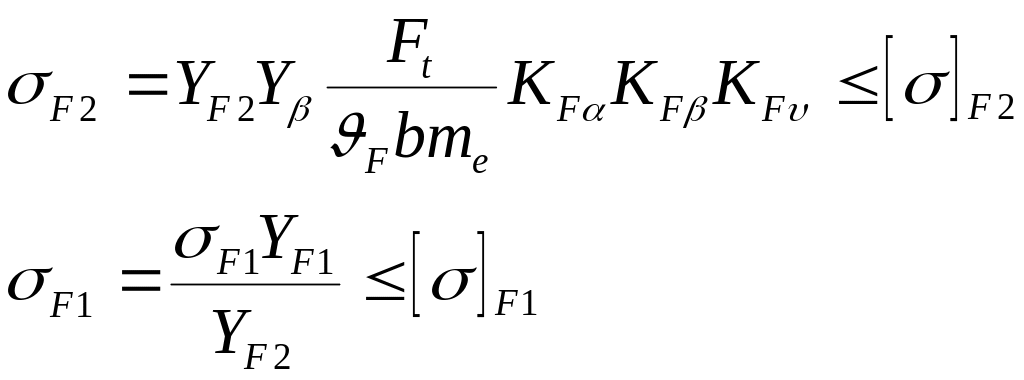
Где К_Fα=1 – коэффициент, учитывающий распределение нагрузки между зубьями прямозубых колес;

К_Fυ – коэффициент динамической нагрузки. Определяется аналогично К_Нυ;

Y_F1 и Y_F2 – коэффициенты формы зуба шестерни и колеса. Определяются по табл. 4.7 интерполированием в зависимости от эквивалентного числа зубьев шестерни z_υ1 и колеса z_υ2