IV) Модель Моисеева.

В этом случае производственная функция может быть записана в виде , где А – неизвестная функция от времени, удовлетворяющая дифференциальному уравнению ; при этом функция V характеризует затраты на научные исследования, а – заданная функция. Тогда модель экономики записывается в виде (здесь s₂ означает долю национального дохода, идущую на финансирование научных исследований, сама же величина этих средств равна V):

Выводы.

Наиболее перспективным из рассмотренных подходов к моделированию технического прогресса является последний, хотя вопросы построения функции до сих пор плохо разработаны. Данную модель тоже можно оптимизировать, хотя такая задача гораздо сложнее уже решённых нами здесь (метод имитационного моделирования). Вопрос о применении всех четырёх подходов к решению различных задач будет разрешён в недалёком будущем.

Имитационное динамическое моделирование и применение производственных функций к прогнозированию экономики.

В последнее время для решения задач управления² и анализа функционирования различных систем всё шире применяется метод системной динамики, основы которого разработаны профессором Дж. Форрестером (США) в 50-х годах XX века /6/. Со временем название этого метода исследования было уточнено в форме «имитационного динамического моделирования».

Любую систему (произвольной природы) можно представить в виде сложной структуры, элементы которой тесно связаны и влияют друг на друга различным образом. Так как реальные системы обладают инерционностью, то часть связей может иметь запаздывания, т.е. реакция на изменения будет происходить не сразу, а с некоторой задержкой во времени /8/.

Сложность структуры и внутренние взаимодействия обусловливают характер реакции системы на воздействия внешней среды и траекторию её поведения в будущем: она может стать через некоторое время отличной от ожидаемой (а иногда и противоположной), т.к. с течением времени поведение системы может измениться из-за внутренних причин. Именно поэтому целесообразно предварительно проверять поведение системы с помощью модели, что позволяет избежать ошибок и неоправданных затрат в настоящем и будущем, выработав компенсационные мероприятия по негативным последствиям тех или иных неблагоприятных изменений.

При имитационном моделировании строится модель, адекватно отражающая внутреннюю структуру моделируемой системы; затем поведение модели проверяется на ЭВМ³ на сколько угодно продолжительное время вперед. Это даёт возможность исследовать поведение как системы в целом, так и ее составных частей /16/.

Имитационные динамические модели (сокращённо, ИДМ) используют специфический аппарат, позволяющий отразить причинно-следственные связи между элементами системы и динамику изменения каждого элемента. Модели реальных систем, как правило, содержат большое количество переменных, поэтому их имитация осуществляется на ЭВМ (кроме того, с помощью новых программ процесс моделирования становится наглядным, и пользователь избавлен от необходимости ручного пересчёта многих функций). Существует ряд общих требований, предъявляемых к ИДМ /18/:

а) Модель должна иметь простую математическую форму;

б) Охватывать большое число переменных, не превышая, однако, возможностей ЭВМ;

в) Быть пригодной для отражения непрерывных взаимодействий.

Базовая структура ИДМ включает следующие элементы [Стратегия и тактика А.У., Системный анализ в экономике и организации производства]:

1. Уровень (контейнер, накопитель) характеризует возникающие накопления внутри системы (см. рис. 21а). Это товары, имеющиеся на складе, деньги на расчётном счёте предприятия или в амортизационном фонде; для физической системы – количество жидкости в некоторой ёмкости и т.д.

2. Поток (или темп потока в другой терминологии⁴) отражает мгновенные потоки между уровнями в системе (см. рис. 21б). Темп отражает активность, в то время как уровни измеряют состояние, которое является результатом активности в системе.

3. Функции решений представляют собой формулировку линии поведения, определяющую, каким образом имеющаяся информация об уровнях приводит к выбору решений, связанных с величинами текущих темпов⁵.

4. Связи между элементами (см. рис. 21в) определяют взаимную зависимость элементов (например, входящая связь означает зависимость данного элемента от другого, а исходящая – наоборот, зависимость другого элемента от данного).

а)	б)	в)	г)	д)

Рис. 21.

Имитационная динамическая модель должна разрабатываться в определённом порядке:

а) Составление вербального описания моделируемой системы.

б) Построение диаграммы причинно-следственных связей, возникающих в моделируемой системе.

в) Построение в компьютерной программе диаграммы потоков и уровней, являющейся основой для математического описания выявленных причинно-следственных связей.

г) Математическое описание моделируемой системы, которое представляет собой комплекс взаимосвязанных уравнений, описывающих взаимодействие причинно-следственных связей.

д) Ввод начальных значений переменных и констант для проведения эксперимента над моделью⁶.

е) Проведение машинных экспериментов и анализ результатов.

Рассмотрим применение ИДМ на примере модели экономики страны, описанной в /8/⁷.

Данная модель учитывает производственную деятельность, демографию, научно-технический прогресс, динамику основных фондов. Результат – объём потребления как по стране в целом, так и на душу населения.

В качестве основного показателя оценки деятельности страны за год берется национальный доход Y, представляемый производственной функцией с постоянными пропорциями от стоимости основных фондов и количества работающих:

, (50)

где K – стоимость основных фондов страны в некотором году t, K₀ – эта же величина в начале рассмотрения (t=0);

L – количество работающих в году t, L₀ – начальное значение L;

Y₀ – национальный доход в году t = 0.

Производственная функция вида (50) учитывает только экстенсивный рост производства, когда количество рабочих и стоимость основных фондов (в виде количества станков, рабочих мест) растут пропорционально друг другу. В этом случае в модели отсутствуют качественные изменения в производстве, которые связаны с созданием новых технологий, новой техники, с меньшей материалоёмкостью, энергоёмкостью производства, меньшим процентом брака и т.п. Для учёта таких качественных изменений в производстве необходимо моделировать их в производственной функции.

Как указывают авторы, самым простым способом моделирования НТП является так называемый автономный технический прогресс (в этом подходе считается, что рост эффективности использования ресурсов не зависит от динамики рабочей силы и капиталовложений и «приносится извне»), когда в функции вида (50) вместо коэффициента Y₀ используется коэффициент A(t), характеризующий эффект от затрат на научные исследования. Таким образом, в нашей модели будет использована производственная функция вида (51):

. (51)

Далее, национальный доход Y расходуется в трёх направлениях: капиталовложения (создание новых основных фондов) I, затраты на проведение научных исследований V и потребление C, т.е. можно записать следующие соотношения:

(52)

где s₁ и s₂ – некоторые положительные числа (можно заметить, что в сумме I, V и C составляют Y).

Демографический блок модели характеризуется уравнением экспоненциального роста:

, (53)

где  – темп роста населения (он может быть непостоянным, т.е. меняться с течением времени).

Количество основных фондов K увеличивается ежегодно на величину капиталовложений I и снижается на величину износа (начальное значение K(0) = K₀):

. (54)

Выбытие основных фондов за счёт износа можно задать как фиксированную долю от текущего состояния основных фондов (в нашей модели – это 1% от их общего количества):

. (55)

Последним не определённым элементом модели является величина A: закон определения этой величины неизвестен; авторы /8/ указывают лишь, что величина A удовлетворяет дифференциальному уравнению . Условно считая, что эффект от научных исследований является периодическим, можно записать уравнение для A:

. (56)

Окончательно получаем модель развития экономики:

(57)

Диаграмма причинно-следственных связей модели представлена на рисунке 22. В данном случае, очевидно, величина A «накапливает» величину за все предыдущие периоды времени, т.е. определяется как уровень с входящим потоком.

Аналогично, стоимость основных фондов K определена как уровень с входящим потоком I и исходящим потоком IZNOS.

Обычные переменные величины изображаются в программе Powersim в виде окружностей, а постоянные – в виде ромбов. Параметры, зависящие от времени, автоматически помечаются значком в форме часов.

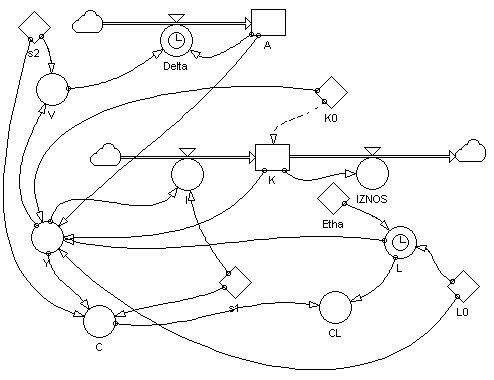
Рис. 22.

Модель задачи в программе Powersim представлена на рисунке 23:

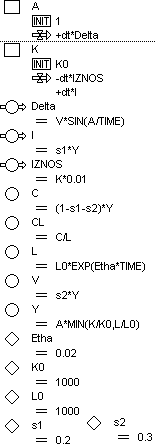
Рис. 23.

Потребление на душу населения CL (не отображённое в основной модели (57)) также показано в модели на рис. 22.

Выходные параметры данной модели при заданных на рис. 23 значениях постоянных, показаны на рис. 24 и 25:

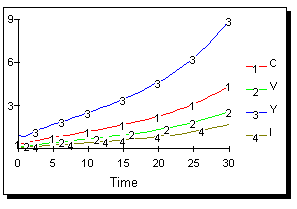
Рис. 24.

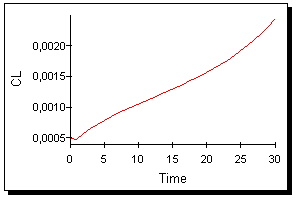
Рис. 25.

Оптимизацию этой модели можно проводить, сравнивая различные варианты управления (например, можно регулировать долю национального дохода, идущую на научные исследования, плавно меняя его с течением времени) экономикой. В качестве критерия оптимальности можно рассматривать, например, потребление на душу населения.

Предположим, что государство намеревается планомерно, в течение 15 лет увеличивать (снижать) долю национального дохода, идущую на научные исследования s₂ (будем считать темп роста населения постоянным, т.е. эти изменения не повлияют на рождаемость или смертность)⁸. Рассмотрим различные варианты, сравнивая между собой динамику потребления на душу населения.

а) Величина s₂ остаётся неизменной, равной 0,3. Очевидно (см. рис. 26), что потребление на душу населения растёт практически линейно.

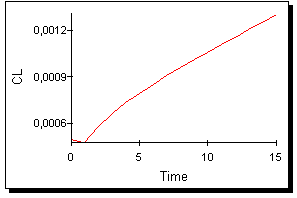
Рис. 26.

б) Величина s₂ снижается линейно по закону , где TIME – время (см. рис. 27). В этом случае, очевидно, есть тенденция к стабилизации потребления на душу населения, а сама величина этого показателя имеет к 15-му году несколько меньшую величину.

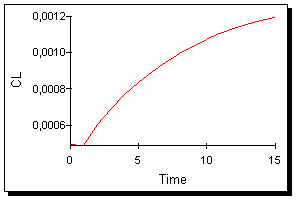
Рис. 27.

в) Величина s₂ растёт линейно по закону (см. рис. 28). В этом случае, очевидно, примерно на 7-8 году наблюдается резкое возрастание темпа роста CL (кривая имеет характерный излом).

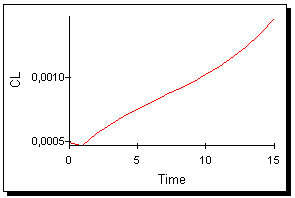
Рис. 28.

Таким образом, меняя всего лишь один управляемый параметр с течением времени, мы можем выбрать более предпочтительный, т.е. оптимальный процесс.

В качестве усложнений модели можно предложить изменение темпа роста населения  с течением времени; особенно интересен случай, когда рост величины s₂ сопровождается и ростом  (см. рис. 29):

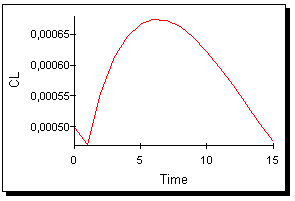
Рис. 29.

Очевидно, на 5-6 году правительство будет вынуждено кардинально решать проблемы, возникшие в государстве, т.к. в противном случае из-за быстрого роста населения люди будут постепенно беднеть.

В более сложном случае (что уже не входит в данную дипломную работу из-за большого количества выкладок) можно рассматривать рост численности населения через рождаемость и смертность как управляемые (в определенных рамках) государством процессы; при этом можно ввести сферу здравоохранения, и др. важные составные части общества (например, повышение качества здравоохранения должно способствовать снижению смертности, а повышение потребления на душу населения – росту рождаемости и т.д.); уровень детализации модели ограничивается только возможностями компьютеров и целями, уровнем проводимых исследований. В некоторых случаях возможны и многокритериальные оптимизации, не сводящиеся только к росту благосостояния народа, но и, например, к максимальному ускорению проведения научных исследований в обществе.