Типичные производственные функции с несколькими ресурсами.

Пусть аргументы ПФ и продукт – нормированы, т.е. , , …  (в этой записи верхний индекс означает не степень от числа, а лишь номер ресурса). Рассмотрим производственные функции, применяемые при использовании более чем двух видов ресурсов.

А) Линейная ПФ . Все ресурсы полностью замещаемы, имеется постоянная отдача от расширения масштабов производства (пропорции между ресурсами роли не играют).

Б) Функция Кобба-Дугласа . Все ресурсы взаимозамещаемы, но ценность ресурса падает при возрастании его доли в общих затратах. Пусть . Тогда при имеется возрастающая отдача от масштабов производства, при – постоянная отдача, при – убывающая отдача.

В) Производственная функция с постоянными пропорциями . Функция непрерывна и не дифференцируема. Увеличение затрат одного из ресурсов при фиксированном количестве остальных – не приводит к увеличению выпуска. Эта ПФ применима в тех случаях, когда имеется один или несколько лимитирующих ресурсов.

Г) Производственная функция с постоянной эластичностью замещения. Перед тем, как давать формулу этой функции, дадим несколько определений.

Предельной нормой замещения одного ресурса (xⁱ) другим (x^j) называется величина , которая показывает, сколько единиц первого ресурса может быть высвобождено при увеличении затрат второго на 1 при условии неизменности результата и постоянства количества всех остальных ресурсов.

Эластичностью замещения одного ресурса другим называется величина . Данная величина показывает, на сколько процентов должно измениться отношение количества одного ресурса к количеству другого при движении вдоль изокванты, чтобы предельная норма замещения изменилась на 1%.

Таким образом, в функции с постоянной эластичностью замещения коэффициент постоянен для всех пар ресурсов и равен . Формула функции выглядит следующим образом: , где  – некоторый показатель однородности.

Предельный переход от одного вида функции к другому в общем виде выглядит следующим образом:

Пусть , тогда:

• при 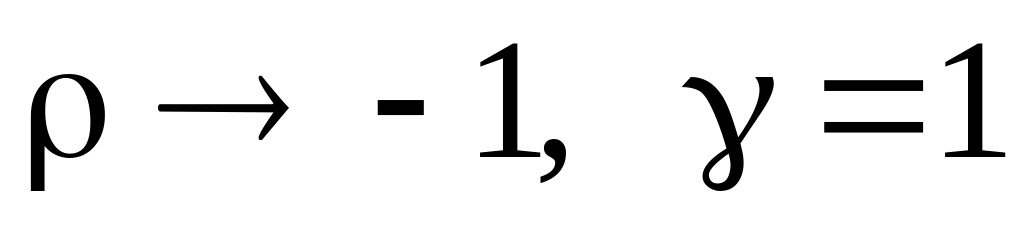получаем линейную ПФ;

• при – ПФ Кобба-Дугласа;

• при – ПФ с постоянными пропорциями.

Модели экономики

Модели народного хозяйства разделяются на дескриптивные модели производства и потребления (производственные функции и функции потребления) и нормативные (балансовые и оптимизационные) модели планирования.

Что касается первого типа моделей, то производственные функции нами уже были рассмотрены, а функции потребления выражаются следующими зависимостями потребления u от дохода v:

а) Предметы первой необходимости , что отражается графической зависимостью примерного вида (рис. 3а):

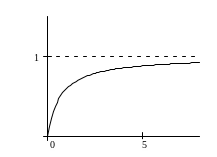
Рис. 3а.

б) Предметы не первой необходимости (см. рис. 3б):

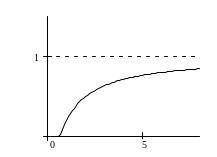
Рис. 3б.

в) Предметы роскоши :

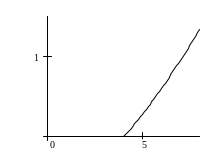
Рис. 3в.

Среди нормативных моделей отметим прежде всего межотраслевой баланс.

Межотраслевой баланс (МОБ) может составляться в натуральном, трудовом или денежном выражении, и представляет собой таблицу связей между отраслями экономической системы. Пусть число отраслей экономической системы равно n. Межотраслевой баланс включает 4 раздела:

I раздел представляет межотраслевые поставки сырья, материалов, полуфабрикатов, топлива и энергии, обусловленные производственной деятельностью отраслей производства.

II раздел отражает конечное потребление отраслей (личное и общественное потребление, не идущее на текущее производственное потребление). Сюда включается возмещение выбытия основных фондов, прирост запасов, личное потребление населения, содержание госаппарата, оборона страны и др.

III раздел включает условно-чистую продукцию отраслей (амортизация, зарплата, прибыль и др.).

IV раздел составлен из перераспределительных отношений в народном хозяйстве через кредитно-финансовую систему (обычно в таблицу этот раздел не вписывается).

Рассмотрим МОБ более детально (в денежной форме).

Межотраслевой баланс

Отрасли	1	2	…	n	Итого	Конечный продукт	Валовый продукт
1	х11	x12	…	x1n		y1	x1
2	х21	x22	…	x2n		y2	x2
…	…	…	…	…	…	…	…
n	хn1	xn2	…	xnn		yn	xn
Итого:			…
Чистая продукция	v1	v2	…	vn
Всего	x1	x2	…	xn

Итак, первый раздел представляет собой первые (n+1) строк и столбцов этой таблицы. Здесь x_ij – производственное потребление j-ой отраслью продукции i-ой отрасли за год (например, первая отрасль может заниматься производством электроэнергии, а вторая – производством угля, тогда x₁₂ – годовые затраты электроэнергии на производство угля).

Здесь i-я строка (x_i1,x_i2,…x_in) – поставки i-ой отраслью своей продукции другим отраслям народного хозяйства, – сумма всех производственных затрат i-ой отрасли – другим отраслям народного хозяйства в год.

j-й столбец (x_1i,x_2i,…x_ni) – использование j-ой отраслью – сырья из других отраслей. – сумма всех производственных затрат i-ой отрасли народного хозяйства за год. – сумма всех производственных затрат всех отраслей затрат за год (промежуточный продукт народного хозяйства).

II раздел – столбцы (n+2) и (n+3): y_i – конечное потребление продукции отраслей (то, что не идёт на текущее производственное потребление). Суммарный (валовой) выпуск отраслей – x_i: ((n+3)-й столбец равен сумме (n+1) и (n+2) столбцов).

III раздел – строки (n+2) и (n+3). Здесь v_j – условно-чистая продукция: .

IV раздел – не заполняется.

Из разложения продукции отрасли на конечный и промежуточный продукт ( ) и разложения продукции отраслей на производственные затраты и условно-чистую продукцию ( ) следует, что или, что то же самое, – суммарный конечный продукт народного хозяйства равен суммарной условно-чистой продукции (т.е. между ними наблюдается баланс).

Оптимизационные модели народного хозяйства.

Среди оптимизационных моделей народного хозяйства отметим простейшую модель экономики, которая позволяет прогнозировать развитие основных показателей экономики страны на 20-30 лет вперёд. Для подобного рода моделей характерно малое число показателей, поскольку при большем их количестве трудно было бы предугадать развитие экономики из-за случайности, непредсказуемости многих параметров.

Обычно модели народного хозяйства включают пять основных блоков: а) блок производственной деятельности; б) блок НТП; в) блок ресурсов; г) демографии; д) социально-экономических механизмов.

Наша модель включает лишь блоки производственной деятельности, НТП и упрощённо – демографии. Краткосрочные и среднесрочные модели планирования являются более детальными.

Итак, основное балансовое соотношение модели можно записать в виде: . Здесь I_t – чистые капиталовложения (средства на расширение производства), C_t – потребление (всё непроизводственное потребление – отдельных лиц, образование, содержание госаппарата, оборона страны и др.), Y_t – национальный доход.

Считаем, что капиталовложения приводят к росту основных фондов (K_t – основные фонды в году t): . Если L_t – число трудящихся в году t, то – производственная функция (с ресурсами L_t и K_t). Часто принимают зависимость численности населения от времени экспоненциальной: ( – темп роста населения).

Пусть s_t – норма накопления, т.е. (распределение средств между накоплением и потреблением): , следовательно, (разумеется, значения s_t должны принадлежать промежутку [0;1]).

Тогда модель можно сформировать в виде:

Эта модель является многошаговой, её параметры – дискретными. Для удобства можно привести её к дифференциальному виду (прежде всего, переходя от разностной формы уравнения к дифференциальному виду, получим ; здесь означает производную по времени). Окончательно получим:

При дезагрегировании (разукрупнении) модели отдельные из этих уравнений разбиваются на части и рассматриваются отдельно, производится их детальное описание.

Если в нашей модели в четвертое уравнение подставить второе, первое – в пятое и т.д. (где это возможно), то модель можно представить в более кратком, упрощённом виде:

Исследование модели.

Введем новые переменные: (фондовооруженность), (потребление на душу населения). Найдём производную от фондовооружённости по времени:

.

Аналогично: .

Таким образом, модель принимает вид:

Пусть , тогда коэффициенты уравнения не зависят от времени t. Возникает вопрос о существовании значений таких, что – так называемых равновесных точек уравнения. Для этого решить уравнение .

Если вспомнить о свойствах производственных функций (возрастание с замедляющимся темпом), то график функции будет выглядеть примерно следующим образом:

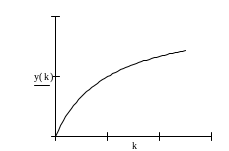
Рис. 4.

Рассмотрим графически решения данного уравнения (см. рис. 5). Очевидно, имеется два решения – и (в нашем примере ):

Рис. 5.

Отметим, что второе из решений существует не всегда (см. рис. 6.). Такое относительное расположение графиков возможно, если .

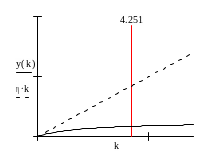
Рис. 6.

Первое, всегда существующее решение (k=0) нас мало интересует, поскольку оно имеет место при полном отсутствии выпуска продукции.

Пусть второе из решений существует. Рассмотрим два промежутка: (до второй точки пересечения графиков – см. рис. 5) и (после пересечения графиков).

а) или (см. рис. 5). Это означает, что значения k растут до тех пор, пока не будет достигнуто значение .

б) : величина k уменьшается до тех пор, пока .

Из обоих случаев (а и б) можно констатировать: равновесная точка устойчива, поскольку значения k стремятся к точке с обеих сторон (возрастание и убывание функции происходит до достижения ).

Если , то и – так называемый режим сбалансированного роста (т.е. с одинаковым темпом растут основные фонды К, национальный доход Y, потребление С, капиталовложения I и население L): всё определяется оптимальной величиной s (долей капиталовложений) и при этом качественных изменений в потреблении не происходит, оно остаётся на душу населения прежним.

Если внимательно посмотреть на рисунок 5 и на уравнение , то можно заметить, что при росте s происходит увеличение числа k^*, а при уменьшении с – k^* убывает.

Выбор наиболее предпочтительного режима сбалансированного роста.

В случае решения данной задачи проблема выбора критерия не решена до сих пор. Пусть критерием будет максимальный уровень потребления на душу населения c.

При сбалансированном росте , при этом определяется из соотношения :

Из уравнений и имеем . Определим максимум этой функции (для этого, очевидно, данная функция должна быть продифференцирована и определена точка, где её производная равна нулю): .

Из условия (определение дифференциала) имеем: .

При этом (из увеличения s следует увеличение k^*, что показано нами выше). Таким образом, из двух сомножителей в выражении лишь или, что то же самое, . Такая точка чаще всего является единственной.

Таким образом, определение искомого значения проводим следующим образом: находим точку k^* из условия , а затем из условия находим .

Итоги.

Потребление на душу населения не растёт, всё изменяется в соответствии с темпом роста населения страны. Можно получить более оптимальный результат, если использовать управление s(t) – норму накопления.

Другие методы оптимизации модели.

Максимизируем суммарное потребление на одного трудящегося за весь период времени t=1,2…T: . Часто берут критерий более общего вида: , где q(t) – заданная функция, соизмеряющая потребление в различные моменты времени ( ).

В качестве необходимого условия зададим (k_T – достаточно большое число).

Тогда задача формулируется так: найти такую форму функции нормы накопления , чтобы с условием максимизировать функцию . Такая задача не всегда имеет решение, поскольку уровень не должен быть слишком высоким. В случае же, если решение имеется, оптимальное управление s(t) состоит в следующем: сначала s(t) выбирается так, чтобы как можно быстрее попасть в точку k^*, затем в течение почти всего периода времени , а в конце периода за минимальное время совершается переход из точки k^* в точку k_T. Таким образом, вновь на большей части промежутка времени имеет место режим сбалансированного роста экономики.

Такое свойство модели называется магистральным, по аналогии с решением следующей задачи:

Необходимо из точки А за кратчайшее время попасть в точку В, при этом в некотором отдалении от точек А и В имеется шоссе. Скорость движения по шоссе во много раз превосходит скорость вне шоссе (см. рис. 7).

Решением в случае данной задачи также будет наиболее быстрое попадание на шоссе из пункта А, затем движение по шоссе в течение большей части времени, а в конце периода времени – наискорейшее попадание с шоссе в пункт В.

Рис. 7.

Окончательные выводы по модели.

Таким образом, экономическая система, в которой производственная функция зависит только от количества основных фондов и числа трудящихся, растёт с темпом, не превышающим темпа роста населения страны. Для исправления этого недостатка необходимо моделирование научно-технического прогресса.

Моделирование научно-технического прогресса.