1.3. Прогнозирование национальной экономики

Прогноз, в общем виде, представляет собой комплекс аргументиро­ванных предположений относительно будущих параметров тех или иных процессов, имеющий вероятностный характер.

Государственное (национальное) прогнозирование - это процесс фор­мирования системы научно обоснованных представлений о направлениях развития национальной экономики, базирующийся на совокупности про­гнозных исследований.

В основе государственного прогнозирования лежит предположение о том, что будущее национальной экономики во многом зависит от ее про­шлого и настоящего. Имея представление о действии объективных эконо­мических законов, исходя из предполагаемых действий различных эконо­мических субъектов, государство может, с определенной степенью досто­верности, прогнозировать будущее состояние социально-экономической системы.

Учитывая то, что будущее и все оценки возможных перспектив связа­ны с элементом неопределенности, в прогнозировании используется веро­ятностный подход. Сущность данного подхода, сочетающего неопределен­ность и детерминированность, заключается в ограничении первого из эле­ментов и описании интервала, в пределах которого возможен поиск регу­лирующих решений.

Важное место в экономическом прогнозировании занимает типологизация прогнозов. Она строится в зависимости от различных критериев и признаков, из которых выделяются важнейшие:

1. По масштабу прогнозирования:

a) макроэкономический и структурный прогнозы;

b) прогнозы развития народнохозяйственных комплексов (топ­ливно-энергетического, оборонно-промышленного, агропро­мышленного и т.д.),*

c) прогнозы отраслевые и региональные;

d) прогнозы первичных звеньев народнохозяйственной системы -предприятий, производственных объединений, отдельных про­изводств.

2. По времени упреждения (см. также табл. 4):

a) оперативные - до 1 месяца;

b) краткосрочные - от 1 месяца до 1 года;

c) среднесрочные - от 1 года до 5 лет;

d) долгосрочные - от 5 до 20 лет;

e) дальнесрочные - свыше 20 лет.

3. По характеру объекта:

a) экономические;

b) финансовые;

c) социальные;

d) научно-технические и т.д.

4. По способу описания тенденций:

a) трендовые (на основе эконометрических моделей с использо­ванием только одного фактора времени);

b) факторные (на основе эконометрических моделей с использо­ванием различных других факторов) .

5. По способу формирования параметров прогноза:

a) генетические - прогнозы "от настоящего к будущему" (состав­ленные на основе инерционности развития экономики и сфор­мировавшихся в ней устойчивых тенденций);

b) нормативные - прогнозы "от будущего к настоящему" (разра­ботанные на основе подхода, связанного с регулируемостью экономики и исходящего из целей развития, которые жела­тельно достичь в прогнозируемом периоде, т.е. в определении параметров воспроизводства, необходимых для достижения за­данных целей экономического роста).

Табл. 4

Прогнозы и их отличия

Оперативные	Кратко­срочные	Среднесрочные	Долгосрочные	Дальнесрочные
по содержанию
нет существенных количественных изменений	количественные изменения	количественные и качественные изменения		качественные изменения
по характеристике оценок
детальные количественные изменения	количественные изменения	количественно-качественные изменения		качественные изменения на уровне общих закономерностей

Главной задачей национального прогнозирования является согласова­ние результатов прогнозных расчетов, получаемых на основе генетическо­го и нормативного подходов. В процессе прогнозирования выявляются су­ществующие проблемы развития экономики и обосновываются возможные способы их решения. Перечень таких проблем и их значимость могут быть раскрыты в процессе анализа расхождений результатов прогнозных расче­тов, полученных при параллельном использовании двух названных мето­дических подходов. Величина таких расхождений определяет меру слож­ности проблем макроэкономического развития.

В результате выполнения прогнозных расчетов получают следующие варианты развития национальной экономики:

• Пессимистический (экстраполяция сложившихся тенденций на бу­дущее)

• Оптимистический (совпадающий с нормативным прогнозом)

• Система вероятных прогнозов (рабочие гипотезы, составленные на основе генетического и нормативного прогнозов).

Процесс прогнозирования включает следующие основные этапы:

1) анализ сложившихся закономерностей и устойчивых тенденций развития;

2) определение возможных вариантов развития;

3) обоснование главных целей и приоритетов развития национальной экономики;

4) выбор способов и ресурсов для достижения поставленных целей;

5) разработка концепции социально-экономического развития

В соответствии с Законом РФ «О государственном прогнозировании и программах социально-экономического развития Российской Федерации" Правительство РФ обеспечивает разработку государственных прогнозов на долгосрочную, среднесрочную и краткосрочную перспективу

Табл. 5

Содержание и этапы разработки государственных прогнозов

Содержание работ	Исполнители
=> Разработка сценарных вариантов разви­тия национальной экономики по на­правлениям	Функциональные ведомства и научные центры
=> Подготовка обобщенных прогнозных параметров по сценариям	Министерство экономического развития и торговли
=> Рассмотрение сценариев развития: по целям, методам, средствам и приори­тетности	Правительство РФ
=> Отраслевые, секторальные и региональ­ные прогнозы	Федеральные органы и субъекты Федерации
=> Уточнение целей, приоритетов развития с у четом ограничений по финансам, ре­сурсам, кадрам	Министерство экономического развития и торговли
=> Разработка концепции социально-экономического развития РФ	Правительство РФ

В процессе государственного прогнозирования задействуется множество ведомств и учреждений: Российская академия наук; Министерства социально-экономического блока, науки и технологий, природных ресур­сов и др.; Государственный комитет по статистике; Центральный банк РФ; институты различных ведомств. Участвуют в данном процессе и субъекты Федерации. Основные этапы разработки государственных прогнозов изо­бражены в табл. 5.

Прогнозирование экономического роста

В разработке прогнозов экономического роста наиболее часто исполь­зуются многофакторные эконометрические модели типа:

где: Y - объем производства;

X₁, Х₂,... Х_n - факторы производства.

Однако в ряде случаев, когда не требуется высокая степень точности прогноза, можно использовать и однофакторные модели. В частности, ши­рокое распространение получили трендовые модели, где единственным фактором выступает время, и модели, характеризующие зависимость объ­ема производства от количества работников.

Методы экстраполяции тенденций (использование трендовых моделей)

Данный метод является количественным и применяется, когда помимо данных измерений некоторой экономической величины Y в дискретные моменты времени имеются еще и теоретические данные о потенциальной форме кривой Y(t), т.е. известно, что зависимость параметра Y от времени t «вписывается» в формулу Y(t)=F(c₁, c₂,…, c_m, t), где величины (c₁, c₂,…, c_m) в нашем случае пока неизвестны. Метод наименьших квадратов, рассматриваемый ниже, представляет собой в некотором смысле «соединение теории с практикой».

Итак, пусть некоторая экономическая величина Y измерена в дискретные моменты времени t₁, t₂, …, t_n: получены её значения y₁, y₂, …, y_n. Известно, что теоретическая зависимость Y(t) должна принадлежать некоторому классу функций F(c₁, c₂, …,c_m, t), т.е. зависимость y(t) известна нам с точностью до нескольких постоянных c₁, c₂, …, c_m. Данные измерений величины Y могут иметь ошибки, не носящие, однако, систематического характера. Требуется подобрать зависимость Y(t) из заданного класса функций с тем расчётом, чтобы ошибка такого подбора была минимальной, т.е. определить значения неизвестных c₁, c₂, …, c_m , лучше всего подходящие проведенным измерениям (t_i, y_i).

В качестве ошибки подбора функции метод наименьших квадратов рассматривает сумму квадратов отклонений значений y_i в каждой точке от значений подобранной функции F(c₁, c₂, …,c_m, t_i):

. (1)

Для минимизации этой функции (дело в том, что значения t_i и y_i для конкретной задачи являются постоянными и в расчёт не принимаются) используются условия (2):

. (2)

Формулы (2) в некоторых случаях (достаточно простой вид функции F(c₁, c₂, …,c_m, t), либо приводимый к линейному виду) позволяют определить недостающие значения c₁, c₂, …,c_m и решить, таким образом, поставленную задачу¹. При найденных значениях неизвестных c₁, c₂, …,c_m мы получаем явный вид зависимости Y(t), что позволяет проводить прогнозирование для произвольных значений t путём подстановки значений t в полученную функцию. Точность прогнозирования будет тем выше, чем меньше мы отклоняемся от точки проведения последних измерений (t_n, Y_n).

Рассмотрим задачу, связанную с линейной регрессией. Пусть имеются данные о ценах на некоторый вид ресурсов в некоторые дискретные моменты времени. Необходимо спрогнозировать значение цен в будущие моменты времени (экстраполяция) и определить, какими (ориентировочно) могли быть цены в моменты времени, когда наблюдения не производились (интерполяция). Зависимость цены от времени считать линейной.

Будем обозначать цену ресурса через P, а время – через t. Тогда функция ошибки  равна:

. (3)

Вычислим её частные производные:

, (4)

. (5)

Преобразовав оба выражения, получим систему линейных алгебраических уравнений:

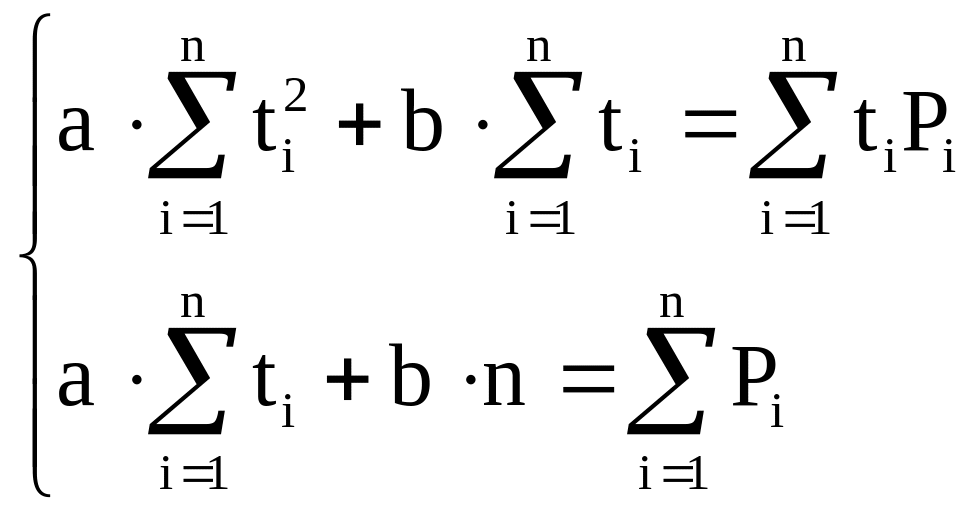(6)

Решим систему (6) методом Крамера, получим:

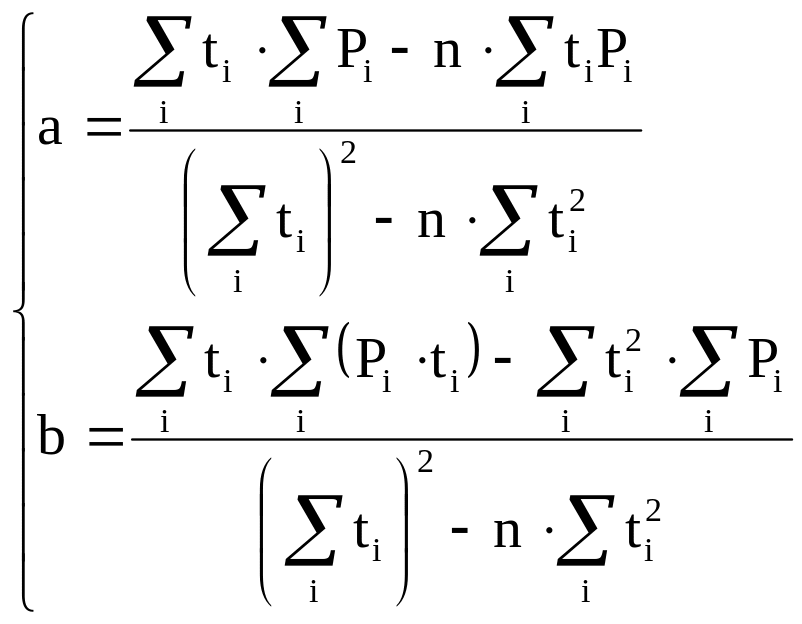(7)

Многие компьютерные программы уже содержат встроенные функции для построения линейных и нелинейных регрессий (например, в системе Mathcad – функции slope и intercept; для построения линейной комбинации произвольных функций – linfit), что избавляет пользователя от их ручного набора. В случае, когда зависимость Y(t) не является линейной, метод наименьших квадратов может не дать требуемого результата из-за сложности получаемых выражений (2) для поиска неизвестных констант c₁, c₂, …,c_m. По этой причине может применяться линеаризация, т.е. сведение нелинейной функции к линейному виду путем алгебраических преобразований.

Линеаризация применяется для построения нелинейных зависимостей при использовании линейной регрессионной модели. В этом случае перед применением формул (7) необходимо провести преобразование координат, которое может быть различным, в зависимости от вида аппроксимирующей функции. Случаев, когда применяется линеаризация, очень много, рассмотрим лишь некоторые из них. Например, зависимость Y(x) может быть:

а) Логарифмической . В этом случае делается преобразование и далее коэффициенты (7) вычисляются для координат (x1, Y).

б) Показательной . Чтобы линеаризовать функцию, нужно прологарифмировать обе части формулы: . Здесь делаются обозначения . Тогда – вновь сформированная линейная зависимость, к которой применимы формулы (7).

в) Дробно-линейной: . Здесь достаточно «перевернуть» функцию, т.е. сделать замену переменной : .

Возможны и другие случаи функции. Для проверки качества построения линейной (или линеаризованной) зависимости можно использовать коэффициент корреляции, который приближается по модулю к 1, когда зависимость близка к линейной. Коэффициент корреляции применяют для новых координат в случае линеаризации, и для исходных – для линейной зависимости. Многое видно и по построению графика.

Применение производственных функций

Производственной функцией называется функция связи между объёмами используемых ресурсов x₁, x₂, …, x_n и результатом производственной деятельности Y: Y=F(x₁, x₂, …, x_n) Иногда для простоты количество ресурсов берут равным двум (количество рабочих и стоимость основных фондов производственной системы). Результат может выражаться количеством единиц выпускаемой продукции, её стоимостью или себестоимостью, возможны и другие варианты. Существует несколько подходов к построению производственных функций, среди которых наиболее распространены функция Кобба-Дугласа , функция с постоянными пропорциями 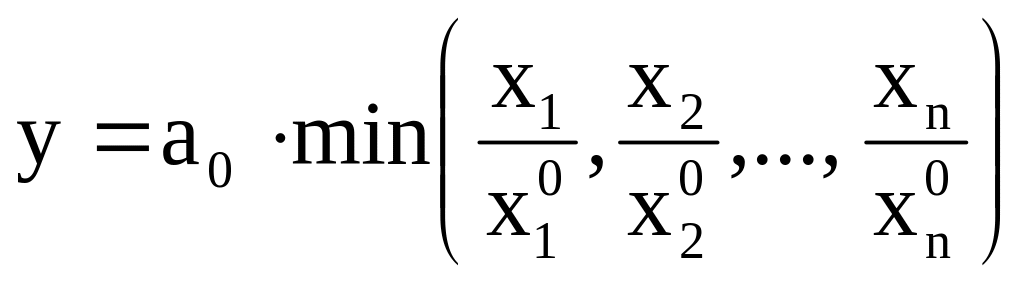и др. Иногда используют и другие типы производственных функций.

Рассмотрим производственную функцию от двух параметров (видов ресурсов): Y = F(K,L), где К – основные фонды, L – затраты труда (число работающих), Y – национальный доход. Перечислим её основные свойства (для простоты мы периодически будем возвращаться к ней, используя данный вид функции наряду со всеми остальными):

1) F(0,L) = F(K,0) = F(0,0) = 0 (выпуск продукции невозможен без наличия хотя бы одного вида ресурсов);

2) , – рост использования одного из ресурсов ведёт к росту результата (национального дохода);

3) , – увеличение использования лишь одного вида ресурсов приводит к снижению эффективности его использования;

4) при  > 1 (положительный эффект от масштаба производства).

Наиболее распространённые производственные функции:

А) Степенная функция . Для двух ресурсов она принимает вид: . Здесь , , К₀, L₀, Y₀ – положительные числа, определяемые при помощи анализа статистической информации. Если при этом  +  = 1, то – функция Кобба-Дугласа (была предложена американскими учёными Коббом и Дугласом). Пусть Y = Y_C = const, тогда – неявная функция связи K и L – изокванта 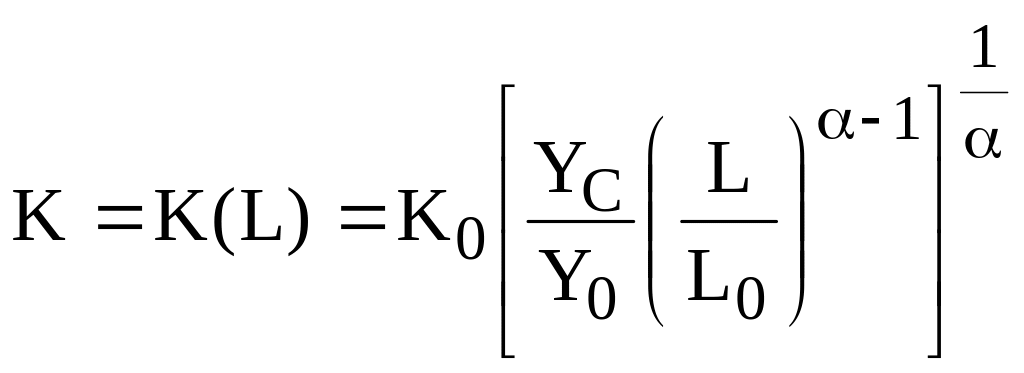. При этом , :

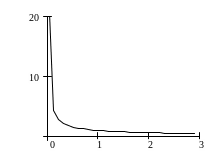
Рис. 1. Типичная изокванта функции Кобба-Дугласа.

Такое положение графика изокванты (при этом следует отметить, что подобный вид имеют все изокванты, лишь приближение графика к осям координат происходит разными темпами) означает, что любое данное количество продукта может быть произведено при сколь угодно малом количестве одного из ресурсов – был бы в достаточном количестве другой. Это существенный недостаток производственной функции, который не отражает реального положения вещей: так, например, для строительства самолёта недостаточно простого избытка рабочей силы – необходим высокообразованный персонал, технология и прочие факторы.

Ещё один недостаток – полная взаимозаменяемость ресурсов в отношении 1:1 (чего лишена следующая производственная функция).

Б) CES-функция или производственная функция с постоянной эластичностью замещения имеет вид: 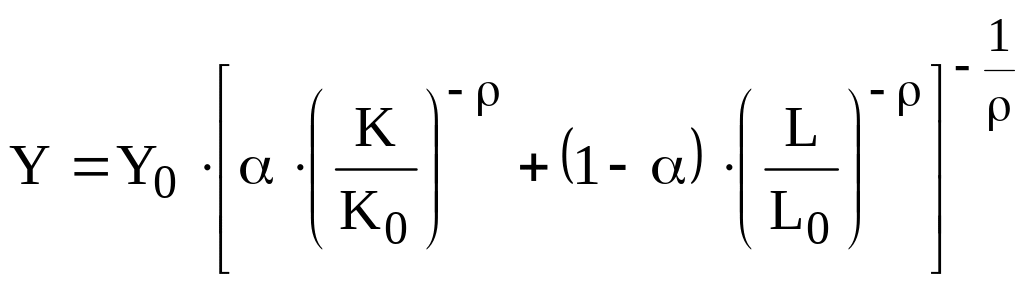. Из свойств данной функции следует, что замещение ресурсов возможно лишь до определённых пределов, а потом увеличение любого из ресурсов практически не даст результата (изокванты функции имеют асимптоты, не являющиеся осями координат, графики изоквант «прижимаются» к осям координат «не вплотную»).

В) Если теперь у функции CES устремить коэффициент  к плюс бесконечности, то мы придём к так называемой производственной функции с постоянными пропорциями или кусочно-линейной производственной функции: . Важным свойством этой функции является наличие разумных пропорций между основными фондами и количеством рабочей силы. Пусть – фондовооружённость в данный момент времени. При этом, если , то дополнительные фонды (по сравнению с фондовооружённостью k₀) пользы не приносят. Если же , то часть рабочей силы также не используется в производстве и пользы также не приносит.

Если взять функцию CES и устремить коэффициент  к нулю, то получится функция Кобба-Дугласа, а если , то выражение преобразуется в кусочно-линейную производственную функцию. Поверхности для двумерных производственных функций и их изокванты приведены на рисунке 2.

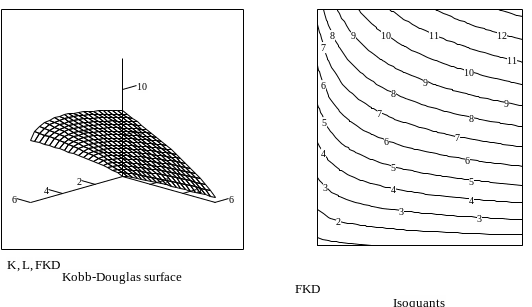
Рис. 2а. Поверхность функции Кобба-Дугласа и её изокванты.

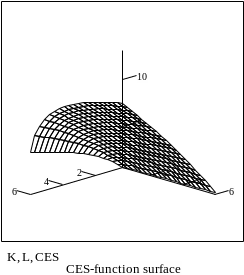
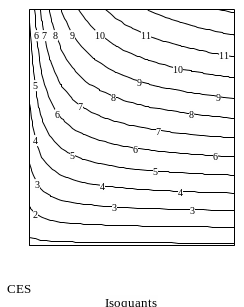
Рис. 2б. Поверхность CES-функции и её изокванты.

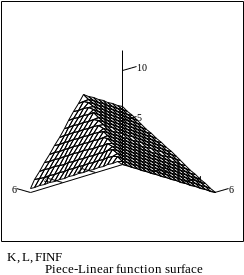
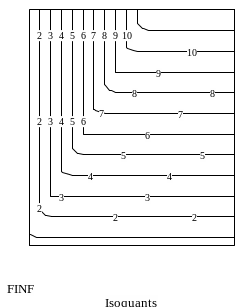
Рис. 2в. Поверхность кусочно-линейной функции и её изокванты.