Кривые Безье
Кривые Безье — это линии особой формы, описываемые тремя или четырьмя точками: начальной, конечной и одной или двумя контрольными. Начальная и конечная точки, как и в случае прямой линии, задают начало и конец кривой Безье, а контрольные точки формируют касательные, определяющие форму этой кривой.
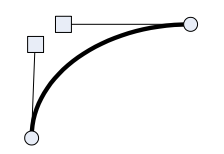
Рис. 17.1. Кривая Безье с двумя контрольными точками
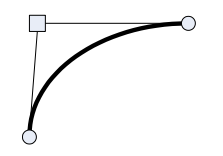
Рис. 17.2. Кривая Безье с одной контрольной точкой
На рис. 17.1 кривая Безье выделена утолщенной линией, ее начальная и конечная точки обозначены круглыми маркерами, квадратные маркеры соответствуют контрольным точкам. Через каждую контрольную точку, а также через начальную и конечную точки кривой Безье проведены касательные (тонкие прямые линии) — они определяют форму кривой. Если мы мысленно переместим какую-либо из контрольных точек, то направление проведенной через нее касательной изменится, и, следовательно, изменится и форма кривой Безье.
На рис. 17.1 представлена кривая Безье с двумя контрольными точками. Такие кривые применяются чаще всего.
Но зачастую предпочтительнее использовать другую, "вырожденную", форму кривых Безье — с одной контрольной точкой (рис. 17.2).
На основе кривых Безье с одной контрольной точкой можно создавать дуги и рисовать секторы, в чем мы вскоре убедимся.
Для рисования кривых Безье с двумя контрольными точками предусмотрен метод bezierCurveTo:
<контекст рисования>.bezierCurveTo (<горизонтальная координата первой контрольной точки>, <вертикальная координата первой контрольной точки>, <горизонтальная координата второй контрольной точки>, <вертикальная координата второй контрольной точки>, <горизонтальная координата конечной точки>, <вертикальная координата конечной точки>)
Назначение параметров этого метода понятно из их описания. Все они задаются в пикселах в виде чисел. Метод не возвращает результата.
Рисование кривой Безье начинается в той точке, где в данный момент установлено перо. После рисования кривой перо устанавливается в ее конечную точку.
Web-сценарий, рисующий кривую Безье с двумя контрольными точками:
ctxCanvas.beginPath();
ctxCanvas.moveTo(100, 100);
ctxCanvas.bezierCurveTo(120, 80, 160, 20, 100, 200);
ctxCanvas.stroke();
Рисование кривых Безье с одной контрольной точкой реализует метод quadraticCurveTo:
<контекст рисования>.quadraticCurveTo (<горизонтальная координата контрольной точки>, <вертикальная координата контрольной точки>, <горизонтальная координата конечной точки>, <вертикальная координата конечной точки>)
Описывать параметры этого метода также нет смысла — их назначение понятно. Все они задаются в пикселах в виде чисел. Метод не возвращает результата.
Рисование такой кривой Безье также начинается в той точке, где в данный момент установлено перо. После рисования кривой перо устанавливается в ее конечную точку.
Web-сценарий, рисующий кривую Безье с одной контрольной точкой:
ctxCanvas.beginPath();
ctxCanvas.moveTo(100, 100);
ctxCanvas.quadraticCurveTo(200, 100, 200, 200);
ctxCanvas.stroke();
Получившаяся кривая будет иметь вид дуги.
Более сложный пример иллюстрирует листинг 17.3.
Листинг 17.3
ctxCanvas.beginPath();
ctxCanvas.strokeStyle = "red";
ctxCanvas.fillStyle = "red";
ctxCanvas.moveTo(100, 100);
ctxCanvas.quadraticCurveTo(200, 100, 200, 200);
ctxCanvas.lineTo(100, 200);
ctxCanvas.lineTo(100, 100);
ctxCanvas.fill();
Web-сценарий из листинга 17.3 рисует красный сектор окружности с красной же заливкой. Мы проводим кривую Безье с одной контрольной точкой, имеющую вид дуги, и соединяем ее начальную и конечную точки с центром воображаемой окружности.
Задание 4. Реализуйте Web-сценарий из листинга 17.4, рисующий прямоугольник со скругленными углами. В виде комментариев допишите происходящее в каждой строке кода.
Листинг 17.4
