3.Расчет статически неопределимых ферм.

Статическая неопределимость фермы может возникнуть, если:

1)отказаться в расчетной схеме от введения в узлы шарниров;

2)в ферме имеются лишние стержни или опоры.

Шарниры в узлах расчетной схемы отражают действительную работу конструкции с гибкими элементами. Поэтому рассмотрим только те случаи возникновения статической неопределимости, которые связаны с наличием лишних связей.

Различают внешне и внутренне статически неопределимые фермы.нешне статически неопределимые фермы имеют лишние по сравнению со статически определимой балкой опорные элементы. Ферма на рис.2.15,например, дважды статически неопределима ( внешне).

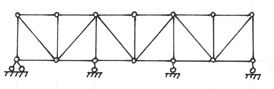
Рис.2.15

Внутренне статически неопределимые фермы имеют лишние (по сравнению с простой фермой) элементы решетки. На рис.2.16 показана шесть раз статически неопределимая ферма (внутренне).

Рис.2.16

Порядок расчета

1. Определяют степень статической неопределимости (ССН).

В ферме с шарнирными узлами проще всего это можно сделать по формуле

ССН = С + С₀ -2k , ( 18.2 )

Где С – число стержней, С₀ - число опорных стержней ( связей ), k – число узлов.

2. Выбирают основную систему для расчета методом сил: отбрасывают лишние опоры, если ферма внешне статически неопределима, или разрезают лишние внутренние элементы так, чтобы превратить ферму в неизменяемую статически определимую систему. По направлению отброшенных связей прикладывают неизвестные продольные усилия Х_{i .}

3. Записывают канонические уравнения метода сил.

. . . . . . . . . . . . . . . . . . . . ( 19.2 )

4.Вычисляют коэффициентss и свободныt члены канонических уравнений.

4.1. Последовательно рассчитывают ферму – основную систему на силы Х_i =1. ( Если ферма имеет n лишних стержней, то ее рассчитывают n раз) Определяют усилия во всех стержнях N_i . Если основная система симметричная, то, естественно, рассчитывают лишь половину фермы.

4.2. Рассчитывают ферму- основную систему на заданную нагрузку. Находят усилия N_Р .

4.3.Перемещения и определяют, используя интеграл Мора для систем с элементами, работающими только на растяжение- сжатие.

( 20.2 )

( 21.2 )

Здесь суммирование ведется по всем стержням, l_n – длина n – ого стержня, А_n – площадь сечения n – ого стержня.

Так как стержни верхнего пояса, решетки и нижнего пояса могут иметь разные жесткости, то удобно искать перемещения, умноженными на некоторую произвольную жесткость ЕА₀

ЕА_{0 =} ( 22.2 )

EA₀ ( 23.2)

5. Решая систему уравнений ( 19.2 ), определяют усилия в отброшенных связях (стержнях) X_i .

6. Расчетные значения усилий в элементах статически неопределимой фермы определяют по формуле

( 24.2)

7.Проверка правильности расчета: ищут перемещение ,которое заведомо равно нулю, например, по направлению одного из отброшенных стержней. Для этого нужно взять интеграл

ЕА₀ (25.2)

Если сумма равна нулю, то расчет верен.

Приведенный алгоритм расчета удобно укладывается в табличную форму

Вопросы для самоконтроля

1.Какие фермы статически неопределимы?

2.Как определить степень статической неопределимости ферм?

3.Как выбрать основную систему при расчете статически неопределимой фермы методом сил?

4.Каков порядок расчета ферм методом сил?

5.Как определяются коэффициенты и свободные члены канонических уравнений?

6.Как проверить результаты расчета?