5.Порядок расчета рам методом сил с несколькими неизвестными.

1.Определяют степень статической неопределимости системы.

2.Выбирают основную систему

3.По направлению отброшенных связей прикладывают неизвестные усилия Х_i .

4.Записывают систему канонических уравнений, каждое из которых имеет простой физический смысл: перемещения в основной системе по направлению отброшенных связей от заданной нагрузки и неизвестных Х_i равны нулю.

Таких уравнений можно записать столько, сколько раз система статически неопределима, то есть сколько она имеет лишних связей. Для системы с n лишними связями система канонических уравнений метода сил имеет вид:

( 16.1 )

Коэффициенты этих уравнений - перемещения в основной системе по направлению отброшенных связей от действия единичных сил – обладают следующими свойствами.

На основании теоремы о взаимности перемещений

(17.1)

Отсюда следует, что матрица коэффициентов симметрична относительно диагонали, образованной коэффициентами с одинаковыми индексами .

Коэффициенты с одинаковыми индексами всегда положительны и не равны нулю, так как получаются умножением эпюры М_i самой на себя.

Коэффициенты с разными индексами могут быть положительными, отрицательными или равными нулю.

Для проверки правильности вычисления коэффициентов руководствуются правилами, с которыми можно познакомиться по учебнику.

5.Вычисляют коэффициенты и свободные (грузовые) члены канонических уравнений. Для этого следует проделать следующую работу.

5.1.В основной системе от заданной нагрузки строят эпюру М_Р (грузовую эпюру).

5.2.Последовательно,прикладывая к основной системе усилия Х₁=1,

Х₂= 1…Х_n=1,строят n единичных эпюр.

5.3.Вычисляют коэффициенты и грузовые члены канонических уравнений по формулам ( 6.1 ) и ( 7.1 ), используя способ Верещагина. На сложных участках целесообразно применять формулу для перемножения трапеций ( 12.1 ) или формулу Симпсона ( 13.1 )

6. Решают систему канонических уравнений, находят Х₁ , Х₂ …Х_n .

7. Строят окончательную эпюру изгибающих моментов М.

Это построение удобно провести в два этапа.

7.1. Строят так называемые “исправленные” эпюры, умножая ординаты единичных эпюр М_i на найденные значения X_i : M₁X₁,…M_nX_{n .} Если при решении канонических уравнений усилие Х_i получилось отрицательным, то ординаты исправленной эпюры откладывают со стороны противоположной ординатам единичной эпюры.

7.2 Окончательную эпюру М получают , суммируя по точкам грузовую эпюру и исправленные:

М = М_Р + M₁X₁ +M₂X₂ + … + M_nX_n ( 18.1)

8. Проверяют правильность окончательной эпюры М, перемножая эпюры М и М_S (9.1) 9. Строят эпюру поперечных сил Q, используя формулу Журавского.

10.Строят эпюру продольных сил N, рассматривая равновесие узлов.

11. Проверяют равновесие системы в целом.

Пример расчета рамы с двумя неизвестными.

Дано: статически неопределимая рама (рис.1.21) и задано соотношение моментов инерции сечений ее элементов I₁ : I₂ = 3 : 4.

Требуется построить эпюры изгибающих моментов М, поперечных сил Q и продольных сил N.

1 Определяют степень статической неопределимости рамы (ССН).

ССН = 5 – 3=2, (19.2)

где 5 – число независимых опорных реакций,

3 – число уравнений статики на плоскости.

2.Основная система показана на рис.1.22

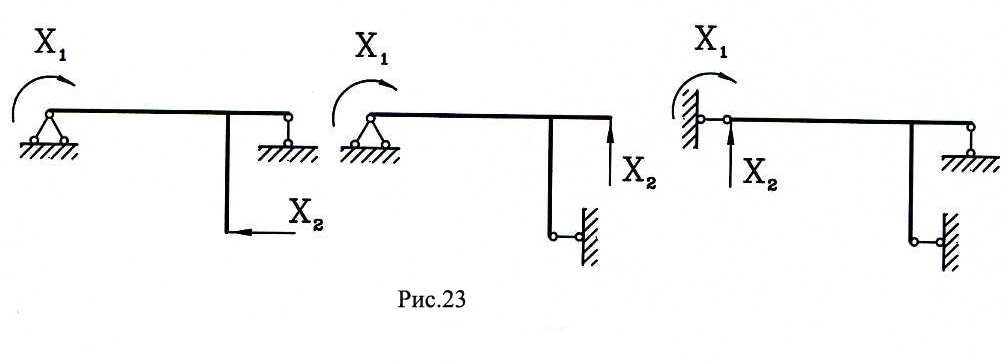
В рассматриваемой задаче возможны и другие варианты основной системы, показанные на рис.1.23.

В выбранной консольной основной системе (рис.1.22) грузовая и единичные эпюры моментов могут быть построены без вычисления опорных реакций, только на основании одного лишь определения изгибающего момента в сечении.

Если основная система балочного или арочного типа, то необходимо привести все расчеты, связанные с построением эпюр.

3.Канонические уравнения:

(20.1)

Здесь и -неизвестные усилия (реакции) в отброшенных связях.

4. Определение коэффициентов и грузовых членов канонических уравнений.

4.1.На рисунках 1.24 и 1.25 показаны единичные эпюры моментов М₁ и М₂ и

эпюра изгибающих моментов от заданной нагрузки М_Р (рис 1.26.)

4.3. Вычисление коэффициентов и свободных (грузовых) членов .

Рис.1.26

Так как элементы рамы имеют разную жесткость на изгиб, то при вычислениях вводят условную жесткость , учитывая заданное соотношение моментов инерции = 3 : 4. Жесткость вертикального элемента примем равной , а ригеля - .

Раму разбивают на участки, на которых перемножаемые эпюры изображены прямыми линиями или очерчены по параболе.

Для определения перемещений применим способ Верещагина.

(Точное положение центра тяжести трапеции на участке А1 определять не нужно, так как где бы он не находился внутри площади трапеции, ордината под ним в эпюре М₂ будет постоянна).

Знак минус перед произведением объясняется тем, что площадь трапеции в эпюре М₁ и ордината под ее центром тяжести в эпюре М₂ лежат по разные стороны элемента А1.

При вычислении грузовых членов и на участке А1 применим формулу (12.1), а при вычислении на участке 1В – формулу (13.1)

= 5. Решают систему канонических уравнений, находят неизвестные усилия X_i .

5,33 X₁ –3,75 X₂ –4,625 = 0

-3,75 X₁ +3,88 X₂+0,9166=0

X₁=2,18

X₂=1,865

6.Строят окончательную эпюру М=М_Р + М₁ X₁ +М₂ X₂.

6.1. Вначале строят исправленные эпюры М₁ X₁ и М₂ X₂ (Рис.1.27)

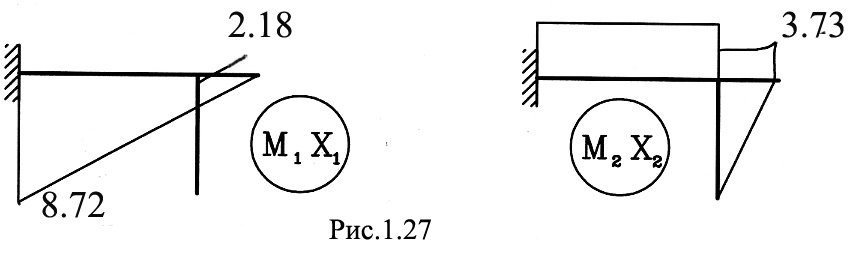
Если найденное усилие X_i получилось со знаком минус. то соответствующая исправленная эпюра должна быть построена на противоположных, чем эпюра М_i, сторонах элементов рамы.

6.2 Окончательная эпюра моментов М получается аккуратным сложением ( по точкам) исправленных и грузовой эпюр.(Рис.1.28)

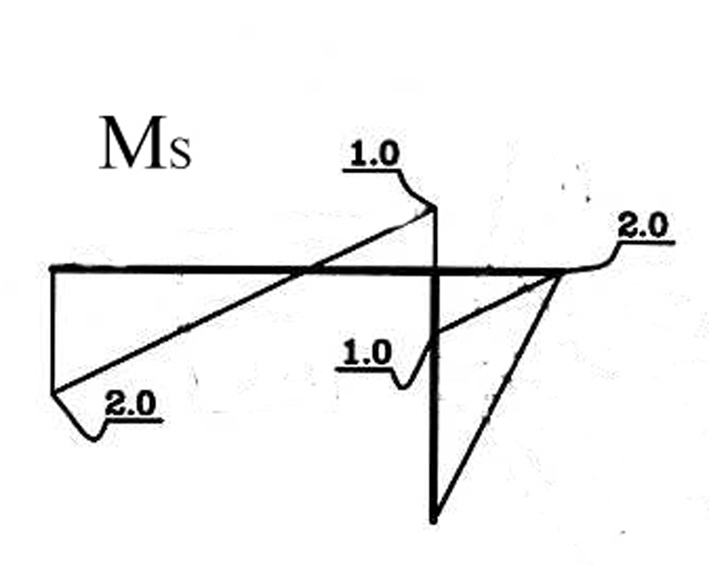
7. Проверка эпюры М.

На рис.1.29 показана суммарная единичная эпюра М_S= М₁+М₂

При перемножении эпюр M и M_S применяем формулы (12.1) и (13.1)

Рис.29

Ошибка счета составляет всего

8. Строят эпюру поперечных сил Q. (См. указания к построению этих эпюр на стр.12)

Эпюра поперечных сил показана на рис. 1.30

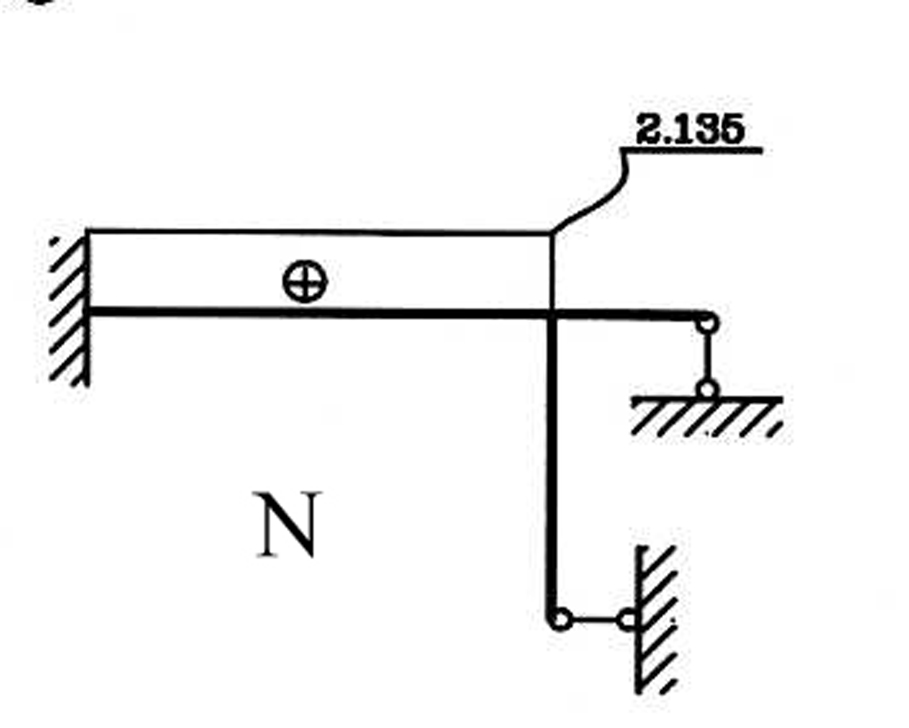
9.Строят эпюру продольных сил N .

Продольные силы находят из равновесия узлов рамы.

Вырежем элемент рамы у опоры С (Рис.1.31)

.

Вырежем узел 1. (Рис.1.32) Рис.1.32

2,1765+3=0,

Эпюра N показана на рис.1. 33

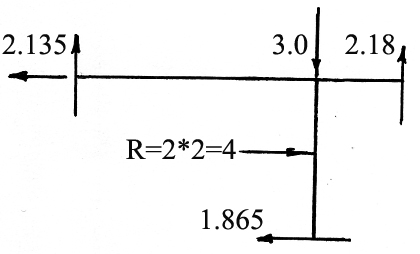
10. Проверка общего равновесия рамы.

Раму отрезают от опор и в местах разрезов прикладывают значения N и Q с полученных эпюр. Эти усилия должны находиться в равновесии с действующей на раму нагрузкой.(Рис.1.34) Рис.1.33

Рис.1.34

Вопросы для самоконтроля

1.Какие внутренние усилия являются предметом поиска при решении задач строительной механики?

2.Каков путь рассуждений при расчете стержневой конструкции на прочность?

3.Какие стержневые системы называют статически неопределимыми?

4.Каковы основные свойства статически неопределимых систем?

5.Какое объяснение можно дать понятию “лишние связи” ?

6.Какова основная идея метода сил?

7.Что принимают за неизвестные при расчете стержневой системы методом сил?

8.Что представляет собой основная система метода сил?

9.Физический смысл канонических уравнений метода сил?

10.Какой физический смысл имеют коэффициенты и свободные (грузовые) члены канонических уравнений метода сил?

11.Как вычисляют коэффициенты и свободные члены канонических уравнений при расчете рам?

12.Как определяют неизвестные X_i ?

13.Какова последовательность построения окончательной эпюры изгибающих моментов М ?

14.В чем состоит проверка правильности окончательной эпюры М ?

15.Как проводится статическая проверка правильности эпюр М, Q и N?