5. Физическая сторона задачи. Матрица жесткости системы

На основе закона Гука устанавливают связь между усилиями и деформациями. Искомые усилия – это моменты М в рассматриваемых сечениях, а деформации - углы поворота каждого из этих сечений. Эта связь устанавливается на основании закона Гука и может быть представлена в виде

М_n = к_n , ( 12.4 )

М_n и к_n – векторы момента и матрица жесткости в n – ом стержне

Эту связь легко установить, если помнить о характере и величине моментов от единичных воздействий на балку, приведенных в таблице на стр.42-43.

10

2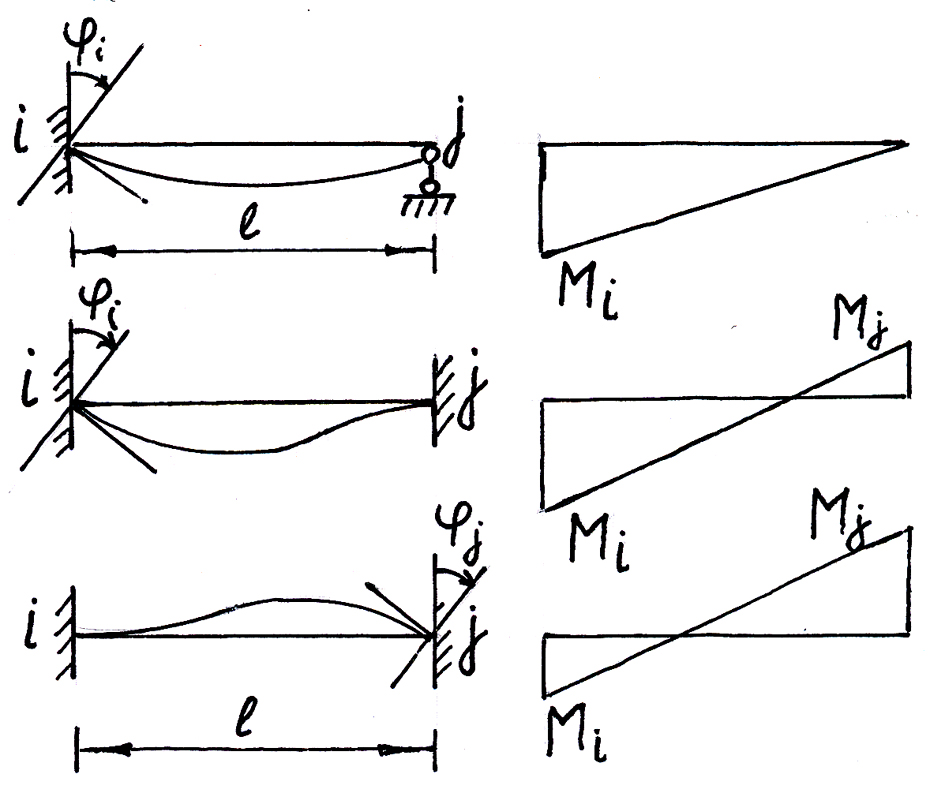

Рассмотрим типовые случаи.

а) Стержень с одним заделанным и другим шарнирно опертым краем (рис.4.9а).

М_i = . ( 13.4 )

Следовательно, коэффициент жесткости к_i равен

к_i = ( 14.4 )

б) Балочный элемент с заделанными краями (рис.4.9б)

Опорные моменты М_i и М_j можно получить, Рис.4.9

Суммируя моменты от поворота сечения i на угол , а сечения j на угол .

М_i = , ( 15.4 )

М_j = ( 16.4 )

В матричной форме можно записать

М_n = [ M_i M_j]^Т = , т.е. к_n = ( 17.4 )

Если система (рама) состоит из нескольких стержней, то эта зависимость может быть представлена так:

М_i = к , (18.4)

М_i = [ M₁ M₂ M_m ] – вектор моментов в сечениях m,

=[ … ] – вектор деформаций (поворотов) этих сечений,

к– матрица жесткости всех элементов системы (ее называют и матрицей внутреннейьжесткости).

При последовательной нумерации концевых сечений всех элементов матрица к оказывается квазидиагональной, на главной диагонали которой располагаются матрицы жесткости отдельных элементов.

к = ( 19.4 )

Матрица к– квадратная, симметричная относительно главной диагонали, а порядок ее равен числу искомых моментов (расчетных сечений).

Составим матрицу жесткости в рассматриваемом примере. Вначале запишем матрицы для каждого элемента в отдельности.

к_АВ = , ( 20.4 )

так как элемент АВ в основной системе (рис.2) – это стержень с двумя заделанными краями.

Остальные элементы – стержни с одним заделанными и другим шарнирно опертым краем. Поэтому

к_ВС к_ВЕ = к_DE = ( 21.4 )

Теперь можно записать матрицу жесткости ( или матрицу внутренней жесткости) для всей рамы:

к= EI . ( 22.4 )

6. Порядок расчета рамы матричным методом перемещений.

Запишем еще раз основные уравнения, отражающие три стороны задачи в матричной форме:

Уравнения равновесия

Р = А М_i. (23.4)

Геометрические уравнения (уравнения неразрывности деформация)

= В Z = А^Т Z (24.4)

Физические уравнения

М_i = к (25.4)

Подставив (24.4) в (25.4), получим

М_i = кА^Т Z (26.4).

Подставив (26.4) в (23.4) получим

Р = А кА^Т Z (27.4)

Матричное уравнение (27.4) эквивалентно системе канонических уравнений классического метода перемещений: Z – искомые перемещения узлов, р грузовые члены. Матрица ( матрица внешней жесткости)

К = А кА^Т ( 28.4 )

представляет собой выражение, каждый член которого равен реактивному усилию в связях по направлению перемещений Z = 1.Уравнения (27.4) можно записать и так

Р = К Z. (29.4)

Определение Z из этой системы уравнений обращением матрицы – дело трудоемкое. Поэтому практически Z находят непосредственно из решения этой системы.

После нахождения Z определяют окончательные значения моментов в расчетных точках по формуле

М_ок = М_Р + М_i = М_Р + кА^Т Z (30.4).

Завершим расчет рамы, показанной на рис. 4.1 После построения всех необходимых матриц работа в первую сводится к составлению матрицы К

Вычислим вначале матрицу кА^Т

кА^Т = (31.4)

Вычислим матрицу АкА^Т _.

АкА^Т = EI (32.4)

Решая систему уравнений

, (33.4)

получаем значения Z₁ и Z₂

Z₁ = - 0.939/EI, Z₂ = 10.43/EI (34/4)

По формуле 26.4 находим моменты в расчетных сечениях от узловой нагрузки

M_i =kA^T Z = (35.4)

Получим окончательные значения изгибающих моменты в расчетных точках

M_ок = M_P + M_i = (36.4)

Значения моментов в расчетных точках с большой степенью точности совпадают с полученными значениями для этой задачи в главе 3, Рис.3.21