116

Московская государственная академия коммунального хозяйства и строительства

Кафедра строительной механики

Колкунов Н.В.

Пособие по строительной механике стержневых систем

ЧастьIi

Статически неопределимые системы. Устойчивость. Динамика

Москва 2009

Пособие предназначено для студентов строительных специальностей заочной формы обучения.

Кратко изложены основные положения метода сил и метод перемещений, приведены элементы динамики и устойчивости сооружений.

Примеры расчета снабжены необходимыми сведениями из сопротивления материалов..

Метод конечного элемента и расчеты на ЭВМ ориентированы на применение программы “Радиус”, которую студенты осваивают при непосредственной работе на кафедре или в классах электронной техники академии.

Глава 1

Расчет статически неопределимых систем методом сил

1.Степень статической неопределимости. Свойства статически неопределимых систем.

Напомним, что статически неопределимой называют такую систему, которую нельзя рассчитать при помощи одних уравнений равновесия. Понятие “рассчитать” сохраняет обычный смысл: нужно найти величины внутренних усилий в каждой точке системы от заданной нагрузки.

Невозможность найти усилия при помощи уравнений равновесия объясняется тем, что статически неопределимые системы содержат так называемые лишние связи (или стержни), не нужные для обеспечения геометрической неизменяемости системы. Понятие “лишние” cвязи весьма условно с точки зрения грамматической. Точнее было бы говорить об избыточных связях. Так, статически определимые системы не имеют лишних связей. Это означает, что удаление любой связи ( стержня) из этой системы , превращает ее в механизм. Поэтому с практической точки зрения статически определимые системы обладают малой надежностью.

Степенью статической неопределимости называют число лишних связей (стержней), которые нужно удалить, чтобы превратить статически неопределимую систему в геометрически неизменяемую статически определимую систему.

Различают внешнюю и внутреннюю статическую неопределимость: система имеет

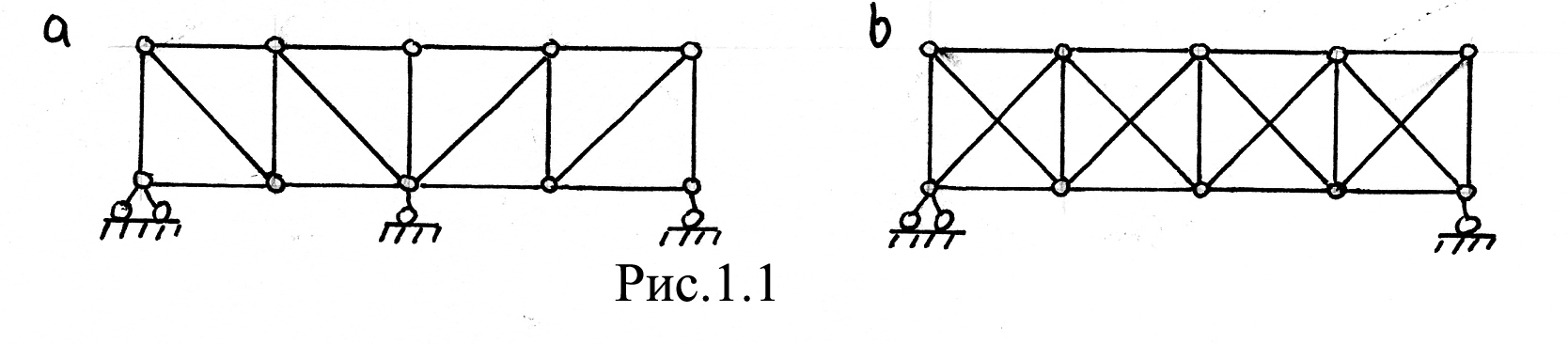
лишние опорные стержни (рис. 1.а) или лишние внутренние стержни (рис.1.б)

Степень статической неопределимости (ссн) – важная характеристика рассчитываемой системы: величина ссн часто определяет техническую трудность расчета.

Простейший способ определения степени статической неопределимости вытекает из определения этой характеристики: ссн можно найти, отбрасывая лишние связи, пока не образуется статически определимая, геометрически неизменяемая система. Ссн равна числу отброшенных лишних связей. Для того, чтобы быстро определять ссн в рамах , нужно хорошо помнить три основные статически определимые системы –:

1) стержень ( в том числе ломаный) опирающийся на одну подвижную и одну неподвижную опору – балочная система (рис.1.2а)

2) консольную систему –один конец заделан, другой свободен (рис.1.22b)

3) трехшарнирную (арочную) систему (Рис.1.2с).

Сравнивая заданную статически неопределимую систему с подходящей статически определимой, нетрудно подсчитать число отбрасываемых связей, то есть ссн.

Исследуем с этих позиций простую раму, показанную на рис.1.3а

Чтобы обратить эту раму в статически определимую систему, нужно отбросить три связи. Это можно сделать по- разному:

1. превращая ее в систему балочную(рис.1.3b): отбрасывая на левой опоре связь, запрещающую поворот сечения, а на правой - две связи, запрещающую поворот и горизонтальное перемещение;

2. превращая ее в консольную систему (рис.1.3с): отбрасывая все связи на правой опоре;

3. превращая ее в трехшарнирную систему, как показано на рис.1. 3d.

Всякий раз в раме нужно отбрасывать три связи.(Перемещения, появляющиеся в раме и соответствующие каждой отброшенной связи, показаны стрелками) Следовательно, степень статической неопределимости рамы равна трем.

Из рассмотренного примера можно сделать полезный вывод : замкнутый контур рамы трижды статически неопределим. На основе этого вывода можно записать формулу для определения ссн в плоских рамах, имеющих к замкнутых контуров:

ссн =3к (1.1)

Рама на рис.1.4а имеет четыре замкнутых контура, ее ссн =12.

Если в раме имеются шарниры, то формула (1.1) приобретает другой вид. Так как введение всякого простого шарнира (Ш) означает устранение одной связи, то можно записать

ссн = 3к –Ш (2.1)

Рама на рис.1. 4.b имеет степень статической неопределимости равную двум:

ссн= 3 1 = 2.

Можно пользоваться и формулой для определения числа степеней свободы системы, помня, что лишние связи (Л) – это “отрицательные” степени свободы

ссн = Л = -W = -3 D + 2 Ш +C₀ (3.1)

D – число дисков (стержней), Ш – число простых шарниров, С₀ – число опорных стержней (связей).

Определим ссн рамы на рис1.4b по формуле (3.1).

D = 2, Ш = 1, С₀ =6.

Ссн = -3 + 2 + 6 = 2.