Метод Эйлера-Коши

Проведем в точке касательную I к функции x(t). Она пройдет под углом .

Пересечение касательной I с вертикалью t_i+1 назовем промежуточной точкой x_i*.

Если предположить, что функция x(t) проходит через промежуточную точку (x_i*,t_i+1), то в ней также можно построить касательную II к функции x(t). Касательная II пройдет под углом .

Проведем через точку (x_i*,t_i+1) прямую III под углом  так, чтобы выполнялось равенство:

.

Через точку (x_i,t_i) проведем прямую IV параллельно прямой III. Она тоже пройдет под углом .

Т очка пересечения прямой IV с вертикалью t_i+1 представляет собой следующую искомую точку (x_i+1,t_i+1) функции x(t).

Рис. 3. Иллюстрация к методу Эйлера-Коши

Осуществим вывод формулы для расчета функции x(t).

Согласно рис. 3:

,

где x_i, x_i+1 – текущая и последующая точки функции x(t) соответственно;

Δx – приращение функции x(t) на интервале Δt.

Величину Δx найдем из прямоугольного треугольника с углом :

.

При малых отклонениях углов  и  можно воспользоваться формулой:

.

Согласно геометрическому смыслу первой производной функции:

,

.

Согласно рис. 3:

,

Величину Δx* найдем из прямоугольного треугольника с углом :

.

Подставив все полученные значения в исходную формулу, получим:

.

Пример:

Для уравнения запишем формулу расчета функции x(t) согласно методу Эйлера-Коши

.

Метод Рунге-Кутта 4-го порядка

Данный метод заключается в том, что рассчитывается последовательность точек функции x(t), причем приращения функции рассчитываются путем усреднения промежуточных коэффициентов К₁, К₂, К₃ и К₄:

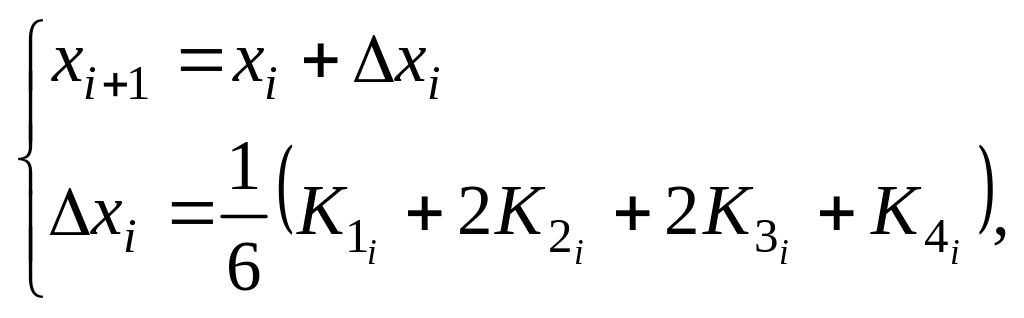
где ,

,

,

.

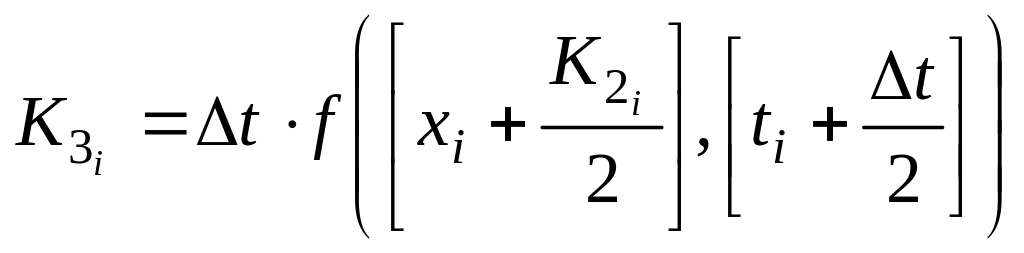Пример:

Для уравнения запишем формулу расчета функции x(t) согласно методу Рунге-Кутта 4-го порядка:

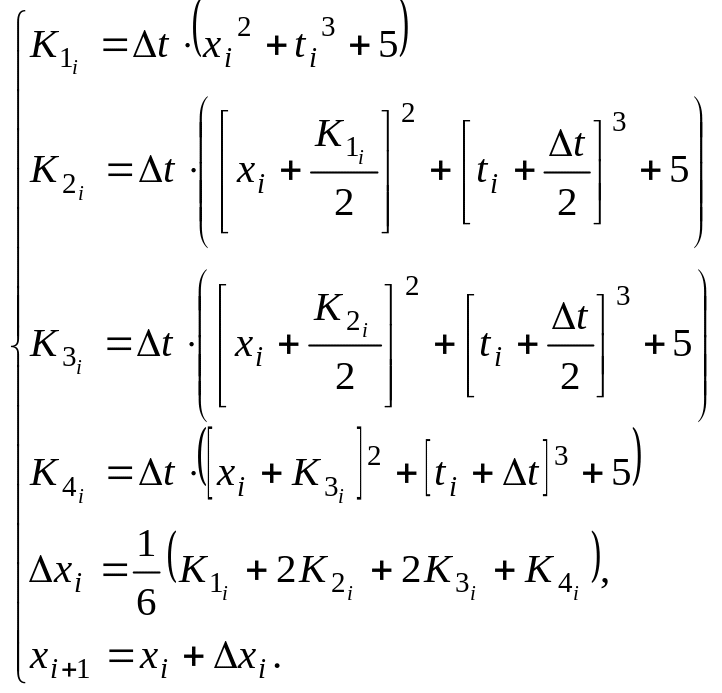
Решение обыкновенного дифференциального уравнения 1-го порядка с помощью функции rkfixed.

Пусть имеется уравнение вида: .

Необходимо найти его решение на интервале [a, b] при начальном условии x(0)=x₀.

В математическом редакторе MathCad существует встроенная функция rkfixed, которая сама осуществляет решение методом Рунге-Кутта 4-го порядка. Использовать её необходимо следующим образом.

Сначала задаются параметры, которые будут передаваться в указанную функцию:

x – вектор начальных условий, в данном случае вектор из одного элемента;

a, b – границы интервала для поиска решения;

n – количество точек на интервале;

D(t,x) – вектор-функция первых производных, в данном случае вектор из одного элемента.

Вызов функции осуществляется так:

rkfixed(x,a,b,n,D)

П

Начальное условие

Правая часть уравнения

Интервал поиска решения

Шаг дискретизации

Число точек дискретизации

Вызов функции

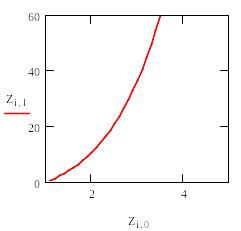
Решение уравнения на интервале (1,5).

Матрица Z имеет 2 столбца и 40 строк.

Первый столбец содержит переменную t, второй – переменную x.

ример:

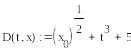
4. Контрольные вопросы

1. Сформулировать задачу Коши 1-го порядка.

2. Воспроизвести и объяснить геометрическую интерпретацию метода Эйлера.

3. Воспроизвести и объяснить геометрическую интерпретацию модифицированного метода Эйлера.

4. Воспроизвести и объяснить геометрическую интерпретацию метода Эйлера-Коши.

5. Привести математическую формулировку решения по методу Эйлера-Коши на конкретном примере.

6. Привести математическую формулировку решения по модифицированному методу Эйлера на конкретном примере.

7. Привести математическую формулировку решения по методу Рунге-Кутта 4-го порядка на конкретном примере.

8. Составить схему алгоритма решения дифференциального уравнения одним из методов.