М инистерство образования и науки рф

ФГБОУ ВПО

«ВОРОНЕЖСКИЙ ГОСУДАРСТВЕННЫЙ

УНИВЕРСИТЕТ ИНЖЕНЕРНЫХ ТЕХНОЛОГИЙ

К АФЕДРА ИНФОРМАЦИОННЫХ И УПРАВЛЯЮЩИХ СИСТЕМ

РЕШЕНИЕ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ 1-ГО ПОРЯДКА ЧИСЛЕННЫМИ МЕТОДАМИ

Методические указания для выполнения лабораторной

работы по дисциплине

«Численные методы»

220400 - «Управление и информатика» (профиль подготовки- «Управление и информатика в технических системах») и

220700 - «Автоматизация и управление» (профиль подготовки-«Автоматизация технологических процессов и производств (по отраслям))»

Для студентов обучающихся по направлению

дневной формы обучения

ВОРОНЕЖ

2012

УДК 519.852.6

Решение обыкновенных дифференциальных уравнений 1-го порядка численными методами: Метод. указания к лаб. работе по дисциплине «Численные методы»/ ФГБОУ ВПО «ВГУИТ».; Сост. С.Г. Тихомиров, Е.А. Хромых,И.А. Хаустов. Воронеж, 2012 – 16 с.

Указания разработаны в соответствии с требованиями, предъявляемыми квалификационной характеристикой ГОС ВПО подготовки инженеров и бакалавров по специальности 220400 и 220700. Они предназначены для закрепления знаний цикла ЕН. Методические указания посвящены обучению решению обыкновенных дифференциальных уравнений 1-го порядка численными методами: методом Эйлера, модифицированным методом Эйлера, методом Эйлера-Коши, методом Рунге-Кутта 4-го порядка с разработкой программ в среде СИ++ и MathCad.

Табл. 3. Библиогр.: 3.

Составители: профессор С.Г. ТИХОМИРОВ,

Доценты Е.А. ХРОМЫХ, И.А. ХАУСТОВ.

Рецензент – профессор, д.т.н. О.Я. КРАВЕЦ

Научный редактор – профессор, д.т.н. В.Ф. ЛЕБЕДЕВ

Печатается по разрешению

Редакционно-издательского совета

ФГБОУ ВПО «ВГУИТ»

 С.Г. Тихомиров,

И.А. Хаустов,

Е.А. Хромых, 2012

• ФГБОУ ВПО «ВГУИТ», 2012

Цель работы:

Освоение численных методов решения обыкновенных дифференциальных уравнений 1-го порядка: метода Эйлера, модифицированного метода Эйлера, метода Эйлера-Коши, метода Рунге-Кутта 4-го порядка с последующей реализацией на ЭВМ.

1. Постановка задачи

1. В соответствии с выбранным вариантом (приложение 1) осуществить решение обыкновенного дифференциального уравнения 1-го порядка 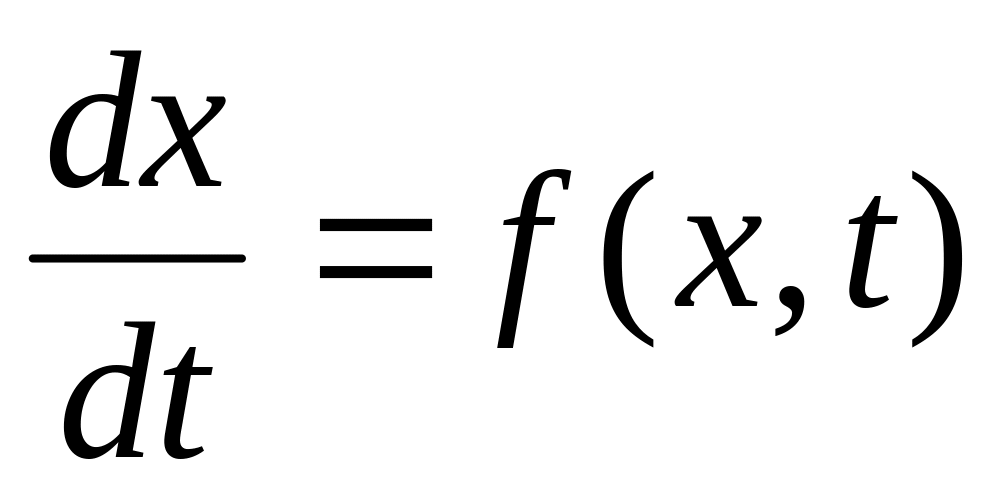на интервале 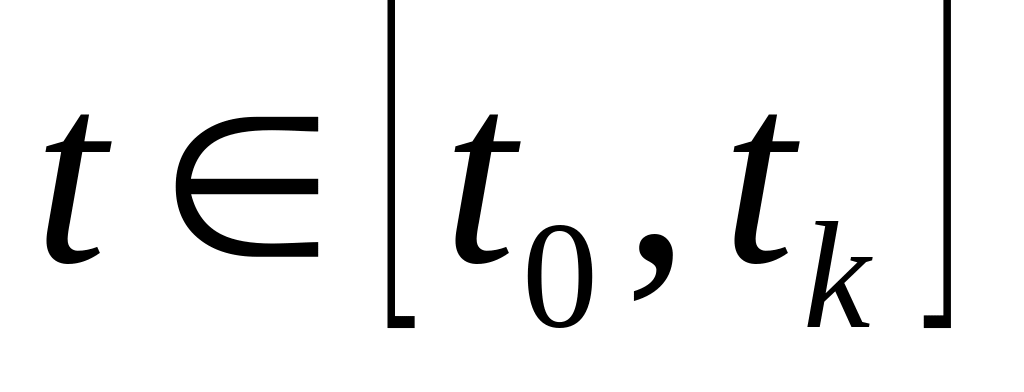с начальным условием x(t₀)=x₀ и временем дискретизации Δt четырьмя методами: методом Эйлера, модифицированным методом Эйлера, методом Эйлера-Коши, методом Рунге-Кутта 4-го порядка.

1.1. Произвести оценку погрешностей метода Эйлера, модифицированного метода Эйлера, метода Эйлера-Коши, рассчитанных относительно решения, полученного методом Рунге-Кутта 4-го порядка по следующей формуле:

.

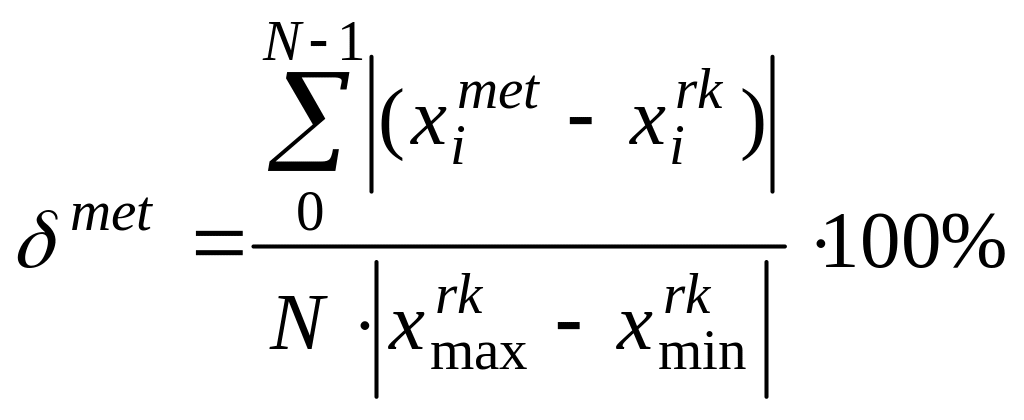где N – число точек решения;

и – решение, полученное по выбранному методу и по методу Рунге-Кутта 4-го прядка на i-м шаге итераций;

и – максимальные и минимальные значения, полученные по методу Рунге-Кутта 4-го прядка.

1.2. Составить алгоритм и программу решения.

2. Дать сравнительную характеристику методов, используемых для решения дифференциального уравнения по следующим характеристикам:

• сложность реализации метода (указать преимущества и недостатки);

• точность метода.

3. Результаты получить в табличном виде:

i
0
N

4. Оформить отчет.