Вопросы

1. Назовите возможные области применения ротационных вискозиметров. Приведите конкретные примеры.

2. В чем заключается принцип работы ротационных вискозиметров? Какие цилиндры называют коаксиальными?

3. Схематично нарисуйте схему течения испытуемого материала в ротационном вискозиметре. Каков характер течения продукта в таких вискозиметрах? Что это дает?

4. Как рассчитать коэффициент динамической вязкости? Как изменится эта формула при постоянном крутящем моменте, приложенном в внешнему цилиндру вискозиметра?

5. Схематично нарисуйте и опишите как различаются ротационные вискозиметры по форме измерительных поверхностей. От чего зависит форма ротора?

6. Опишите известные варианты вискозиметров с коаксиальными цилиндрами. Какие методы исследований при этом реализуются. Возможно ли сочетание методов? При каких условиях?

7. Достоинства и недостатки ротационных вискозиметров с постоянным крутящим моментом и постоянной скоростью деформации.

8. Устройство и принцип действия ротационного вискозиметра системы Воларовича.

9. Устройство и принцип действия ротационного вискозиметра «Reotest–2».

10. Методика расчета реологических характеристик в области неразрушенной структуры продукта.

11. Методика расчета реологических характеристик в области лавинного разрушения структуры продукта.

12. От чего зависит точность измерений с помощью ротационного вискозиметра и как ее повысить?

13. Порядок выполнения измерений с помощью ротационного вискозиметра «Reotest–2».

14. Как рассчитать напряжение сдвига?

15. Что показывает градиент скорости деформации и от чего он зависит?

Практическое занятие № 2 поверхностные свойства пищевых продуктов. Оценка адгезии и внешнего трения сухих молочных продуктов

Цель занятия: изучить

Материальное обеспечение работы. Калькулятор.

Теоретическая часть

Поверхностные свойства пищевых продуктов – адгезия и внешнее трение – проявляются на границе раздела между продуктом и твердой стенкой. Они имеют существенное значение в разнообразных технологических процессах, где возможен контакт между продуктом и стенкой обрабатывающей машины.

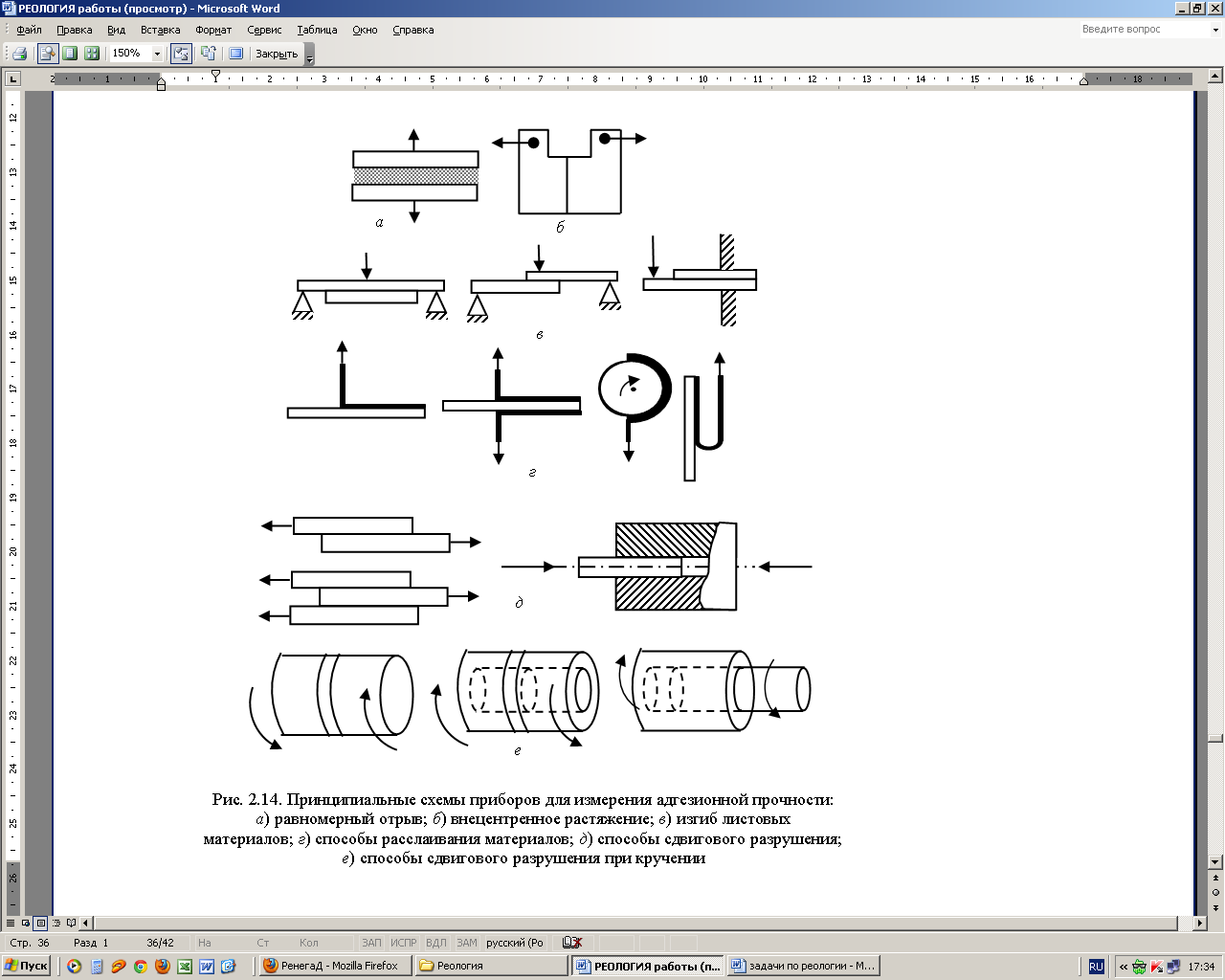
Качественно адгезию можно охарактеризовать двумя способами: нарушением контакта одновременно на всех участках площади (рис. 1 а,г,д) или путем последовательного отрыва отдельных участков – расслаиванием, отдиранием (рис. 1 б,в), оба способа нашли практическое применение. При первом методе разрушающую нагрузку прилагают в направлении как перпендикулярном к плоскости контакта, так и параллельном ей и обычно относят к площади поверхности контакта. При втором методе определяют силу, необходимую для расслаивания склейки, ее относят к единице длинны.

Наиболее часто в адгезиометрах для пищевых продуктов реализуется схема по рис. 1,а. Она может отличаться способами приложения силы и регистрации отрывающего усилия.

Например, в приборе Николаева «мгновенно» отрывается верхний диск с помощью рычажного механизма; в приборе Кульмана постепенно отрывается нижний диск при наполнении подвешенной к нему емкости водой. Разделение контактирующих тел может происходить по трем вариантам: адгезионное – по границе раздела продукт–стенка, когезионное – по слою продукта, и смешанное.

Рис. 1. Принципиальные схемы приборов для измерения адгезионной прочности: а - равномерный отрыв; б - внецентренное растяжение; в - изгиб листовых материалов; г - способы расслаивания материалов; д - способы сдвигового разрушения; е - способы сдвигового разрушения при кручении

Приборы для измерения адгезии должны удовлетворять следующим требованиям:

• не требовать предварительной тарировки на эталонном материале и выражаться в абсолютных единицах;

• обеспечивать изменение усилия и длительности предварительного контакта в широком диапазоне;

• иметь набор пластин разной площади и шаблон для нанесения продукта заданной толщины на пластину;

• позволять легко заменять материал пластин и степень его механической обработки;

• допускать варьирование скорости приложения силы отрыва или сдвига в широком диапазоне.

Классический тип прибора для измерения силы внешнего трения представляет собой пару тел, соприкасающихся плоскими поверхностями, площадь которых может быть от долей квадратных миллиметров до десятков квадратных миллиметров. При этом одно из тел смещается относительно другого. Сила смещения (трения) измеряется тензометрическими, динамометрическими или какими-либо другими датчиками.

Рис. 2. Методы измерения внешнего трения

К первой группе методов определения коэффициента трения относятся такие, в которых одна плоскость поступательно перемещается относительно другой плоскости (рис. 2 а, б, в).

По схеме а продукт перемещается по движущейся исследуемой поверхности, при этом сила трения измеряется динамометром любого типа. Таким, наиболее распростра-ненным методом, определяют трение твердообразных продук-тов: сухарей, хлеба, зерна и т.п.

По схеме б продукт перемещается с помощью груза по исследуемой неподвижной поверхности. Сила трения в этом случае равна минимальной массе груза, необходимой для равномерного перемещения продукта. Этим методом определяют коэффициент трения таких твердых продуктов, как сыр, кондитерские изделия.

По схеме в продукт скользит по наклонной поверхности. Коэффициент трения определяют по минимальному углу наклона α поверхности исследуемого конструкционного материала, по которому скользит пищевой продукт. Такой метод позволил определить статический коэффициент трения сыра, сухарей, сыпучих продуктов. Определение коэффициента трения по углу наклона плоскости, при котором начинается движение продукта по поверхности, недостаточно точно, так как угол наклона плоскости в момент движения определяют приблизительно, к тому же невозможно установить изменение коэффициента трения с изменением скорости скольжения.

Ко второй группе относятся такие методы, при которых одна из фрикционных пар совершает вращательное движение.

По схеме г определяют коэффициент трения конфетных масс. Продукт лежит на вращающемся диске, исследуемый конструкционный материал скользит по вращающемуся продукту. Сила трения определяется по крутящему моменту, передаваемому от диска образцу.

По схеме д продукт, закрепленный на упругой балке, скользит по вращающейся поверхности исследуемого материала. Этим методом определяют коэффициент трения мяса, рыбы, таблеток кофе и чая, сухарных плит, формового хлеба.

К третьей группе относятся методы, в которых образующая цилиндра соприкасается с плоскостью. Схема е – балка, совершающая колебательные движения на двух вращающихся навстречу друг другу роликах.

К четвертой группе относятся методы, в которых одна цилиндрическая или плоская гибкая поверхность перемещается по цилиндрической поверхности (схема ж).

При этом изменение давления допускают методы, изображенные на всех схемах, кроме ж; изменение размера поверхности – методы а–д; изменение скорости скольжения допускают все методы, кроме в.

На внешнее трение влияют те же факторы, что и на адгезию. Следовательно, статическое трение должно быть больше динамического. При первоначальном сдвиге часть усилия расходуется на выход частиц или молекул одного тела из неровностей или молекулярных ям другого, остальное – на разрыв молекулярных и других контактов, которые во время движения не успевают полностью восстанавливаться. Достаточно малая скорость относительного движения трущихся тел может вызывать скачки, т.е. прерывистость движения: тело переходит из одного статического положения в другое, где вновь образуются контакты с поверхностью скольжения. При больших скоростях скольжения и неизменном состоянии поверхности скольжения подобные эффекты обычно не наблюдаются.

Задача №1 –7 . Рассчитайте и определите соотношение между адгезией и аутогезией частиц муки, если известен их средний диаметр (dср.), пористость (П), сила адгезии и аутогезии отдельных частиц (Fад., Fаут.).

Таблица 1

№№ Задачи	1	2	3	4	5	6	7
Средний диаметр частиц, (dср.) мкм.	10	20	30	35	45	55	65
Пористость, П.	0,23	0,27	0,31	0,34	0,37	0,39	0,41
Сила адгезии частиц Fад107 Н.	10,7	8,5	8,1	7,7	7,4	7,1	6,82
Сила аутогезии Fаут.106 Н.	2,3	3,5	4,7	5,2	5,3	5,4	5,6

Задачи № 1 - 7.

Сила аутогезии между частицами муки, медианный диаметр которых составляет 40 мкм, равна 5,510-6Н. Рассчитать силу аутогезии слоя частиц муки в обычных условиях и после слёживания, если пористость (П) муки уменьшилась с 0,46 до 0,2, а сила аутогезии между отдельными частицами возросла в 5 раз. Определить, во сколько раз увеличилась сила аутогезии в результате слеживания.

1. Определяем площадь, приходящуюся на одну частицу

2. Число частиц на 1м2 контакта слоя муки (без слёживания) с учетом пористости

3. Сила аутогезии слоя муки в расчете на 1м2.

4. Число частиц на 1м2 контакта слоя муки (после слёживания) с учетом пористости

5. Сила аутогезии слоя муки (с учетом пористости) после слеживания

6. Сила аутогезии слоя муки увеличилась в результате слеживания в n раз.

раз.

Справочный материал.

Пористость: отношение объёма порового пространства между частицами к объёму сыпучих пищевых масс.

Например: пористость 0,33 означает, что 33% объема пищевой массы занимает поровое пространство, а 67% частицы.

Задача №8 Определите параметры течения сыпучего материала и сделайте вы­вод о характере его течения. Если известна зависимость между усилием сдвига и нормальным давлением при движении внутри муки (1), по отношению к стальной поверх­ности (2), таблица 2.

Таблица 2

1	Рк, кПа	1,25	1,88	2,63	3,31	4,38
	Fτотр.,кПа	1,88	2,25	2,75	3,19	3,75
2	Рк, кПа	1,13	1,88	3,25	4,38	-
	Fτотр.,кПа	0,5	0,88	1,38	1,88	-

Задача №9. Определите параметры течения сыпучего материала и сделайте вы­вод о характере его течения. Если известна зависимость между усилием сдвига и нормальным давлением при движении внутри муки (1), по отношению к полиэтилену ПВД (2), таблица 4.

Таблица 3

1	Рк, кПа	1,25	1,88	2,63	3,31	4,38
	Fτотр.,кПа	1,88	2,25	2,75	3,19	3,75
2	Рк, кПа	1,06	1,88	3,25	4,38	-
	Fτотр.,кПа	0,75	1,00	1,44	1,81	-

Задача №10. Определите параметры течения сыпучего материала и сделайте вы­вод о характере его течения. Если известна зависимость между усилием сдвига и нормальным давлением при движении внутри муки (1), по отношению к токопроводящему ПЭ (2), таблица 5.

Таблица 4

1	Рк, кПа	1,25	1,88	2,63	3,31	4,38
	Fτотр.,кПа	1,88	2,25	2,75	3,19	3,75
2	Рк, кПа	1,00	1,81	2,56	3,25	4,38
	Fτотр.,кПа	0,38	0,625	0,94	1,13	1,5

Задачи №8 - 10.

Когда движение сыпучей массы происходит по поверхности разнородных тел, т.е. осуществляется адгезионное движение, то согласно двучленному закону трения его можно представить следующим образом:

Fтотр.= (FNад. + Рвд.),

где  – коэффициент внешнего трения.

Результаты измерений можно представить прямыми 3 и 3`, коэффициент внешнего трения равен тангенсу угла наклона этих прямых; т.е.

tg = .

Отрезок, отсекаемый на оси ординат, равен сцеплению при адгезии:

Сад. =   FNад.

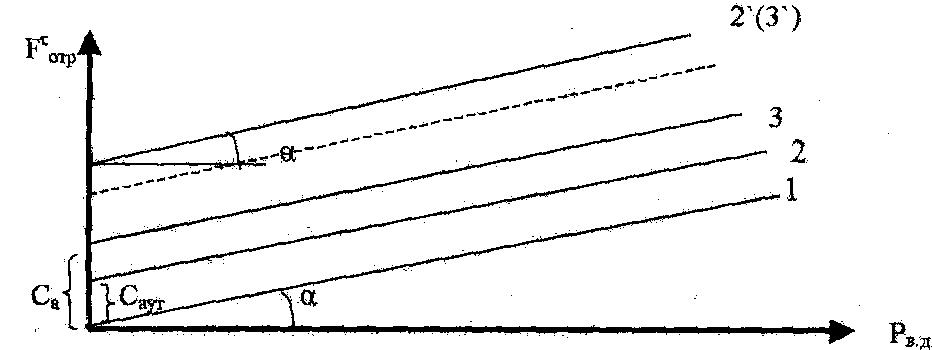
Рисунок 1 - Зависимость сопротивления сдвига Fтотр. от нормальной нагрузки Рв.д.:

1 - при отсутствии адгезии или аутогезии; 2 ,2` - аутогезионный отрыв (движения); 3,3`- адгезионный отрыв (движения).

Прямые 2 и 2` (рисунок 1)отражают аутогезионное движение сыпучей массы, которое аналитически определяется уравнением:

Fтотр.= в(FNаут. + Рвд.)

Отрезок, отсекаемый на оси ординат,в этом случае, равен сцеплению при аутогезии:

Саут. = в  FNаут.

Экспериментальные данные представляют, как показано на рисунке 1, по тангенсу угла  определяют коэффициент внешнего трения уравнения и внутреннего трения при аутогезионном движении сыпучей массы; величины сцепления, (рисунок 1) определяются по известному коэффициенту трения в соответствии с формулами Сад. =   FNад., Саут. = в  FNаут.и по величине отрезка, отсекаемого на оси ординат, рассчитывают FNад., а также FNаут., т.е. адгезию и аутогезию в расчете на 1 м2 поверхности.

Задача №11. В зависимости от влажности теста получены следующие значения модуля Юнга и вязкости:

Таблица 5

Влажность, W,%	Модуль Юнга Е, кПа	Вязкость, 10-3, Пас
32	22,6	1100
44	2,2	3,7
60	0,73	2,8

Используя сведения, приведенные в таблице 10, определить к какому классу структурированных систем относится тесто с различной вязкостью.

Задачи №12 –15 . Для теста в процессе брожения в зависимости от влажности (W) получены следующие данные:

Таблица 6

№№ Задачи	12	13	14	15
Влажность теста W,%	39,7	41,5	43,8	44,5
Период релаксации напряжений , с	15	12	10	8
Вязкость,  кПас	370	443	45	21

Определить модуль Юнга (Е) и его размерность, деформацию () если система деформируется при напряжении, , равном: 0,87 кПа, время деформации 2, 7, 10, 25 (мин).

Задачи №11- 15.

Время релаксации напряжения (λ) представляет собой время, в течение которого начальное напряжение в теле σ0 уменьшилось в е раз (е – основание натурального логарифма). Время релаксации равно: λ=η/Е, где η – вязкость, Е – модуль Юнга.

Классификация пищевых масс по структурно-механическим свойствам.

Таблица 9

Тип структурированных систем	Модуль Юнга Е, Па	Вязкость , Пас	Отношение /Е, с
Свободнодисперсные	меньше 10	меньше 10	меньше 10
Связнодисперсные	10÷104	102÷106	10÷102
Твердые структуры	свыше 104	свыше 106	свыше 102

Задача №16 - 47. Определите среднюю силу сцепления между частицами муки в порошке, если его пластическая прочность на сдвиг Рс, пористость П, структурный параметр k (см. номер задачи в табл. 9). Структурный параметр k определите по таблице 7 диаметр частиц муки равен d=40 мкм.

Таблица 7

Объёмное содержание φ	0,20	0,25	0,30	0,40	0,45	0,50	0,55
Структурный коэффициент k	0,02	0,07	0,24	0,70	1,10	1,60	2,00

Таблица 8

Задача №	Рс, Па	П=1–φ	d, мкм
16	201	0,54	40
17	205	0,55	39
18	207	0,16	41
19	208	0,17	42
20	209	0,18	43
21	211	0,19	44
22	210	0,20	45
23	212	0,21	46
24	213	0,22	47
25	214	0,23	48
26	215	0,24	49
27	216	0,25	50
28	217	0,26	51
29	218	0,26	52
30	220	0,28	53
31	221	0,29	54
32	222	0,30	55
33	223	0,31	56
34	224	0,32	57
35	225	0,33	58
36	226	0,34	59
37	227	0,35	60
38	228	0,39	61
39	229	0,37	62
40	230	0,38	63
41	231	0,39	64
42	232	0,40	65
43	233	0,41	66
44	234	0,42	67
45	235	0,43	68
46	245	0,44	69
47	250	0,45	70

Задачи №16 – 47.

При решении исходят из того, что пластическая прочность Рс структурированных дисперсных систем связана со средней силой сцепления соотношением:

Рс ≈n , где n=к/d2 – среднее число контактов на единице поверхности сдвига; d – диаметр частицы; к – структурный параметр, определяется по таблице для заданного содержания дисперсной фазы.

Задачи №58–67. Для теста с различным содержанием влаги (W,%) Таблица 11 получены следующие данные изменения напряжения (, кПа) от времени (t). Определите время релаксации напряжения (λ), считая, что в данном случае напряжения релаксируют также как в механической модели Максвелла.

Механическая модель Максвелла представляет последовательное соединение элемента жесткости и вязкости. Изменение напряжения сдвига во времени при постоянной деформации описывается следующим уравнением:

.

В логарифмических координатах это уравнение прямой линии:

lnt = ln0 – (1/λ)∙t,

построив графическую зависимость lnt от t, по тангенсу угла наклона прямой можно найти λ-1, а затем и λ – время релаксации напряжения.

Таблица 11

№ Задач	58	59	60	61	62	63	64	65	66	67
W,%	25	30	35	40	45	50	55	60	63	65
t,мин	, кПа	, кПа	, кПа	, кПа	, кПа	, кПа	, кПа	, кПа	, кПа	, кПа
10	8782,524	7713,373	6878,004	6240,383	5310,787	5030,041	4724,977	4369,45	4040,184	3686,152
20	6292,954	5170,428	4365,72	3686,678	2726,649	2462,414	2189,41	1898,955	1627,751	1356,06
30	4509,098	3465,842	2771,081	2178,006	1399,908	1205,454	1014,505	825,2826	655,8052	498,8664
40	3230,91	2323,223	1758,906	1286,717	718,7368	590,1202	470,0908	358,6663	264,2176	183,5227
50	2315,048	1557,303	1116,442	760,1636	369,0118	288,8884	217,8257	155,8757	106,4507	67,51423
60	1658,805	1043,891	708,6463	449,0876	189,457	141,4229	100,9337	67,74332	42,88795	24,8371
70	1188,585	699,7414	449,8036	265,3108	97,27045	69,23241	46,7696	29,44113	17,27914	9,137057
80	851,6587	469,0507	285,5067	156,7397	49,94031	33,89215	21,6716	12,79506	6,961599	3,361336
90	610,2401	314,4141	181,2215	92,59827	25,64021	16,59162	10,04196	5,56071	2,804761	1,236566
100	437,2561	210,7581	115,0279	54,70498	13,16412	8,122288	4,653135	2,416675	1,130011	0,454907
110	313,3077	141,2754	73,01239	32,31847	6,758687	3,976198	2,15612	1,050283	0,45527	0,167351
120	224,4948	94,6997	46,34363	19,09303	3,470025	1,946515	0,99908	0,456451	0,183424	0,061565
140	115,2595	42,55132	18,6714	6,663811	0,914689	0,466484	0,214514	0,086212	0,029774	0,008332