Задания
1. Изучить и законспектировать теоретическую часть работы.
2.Получить вариант задания с данными и построить в масштабе кривые течения в координатах напряжение сдвига – градиент скорости деформации (τ – ) для структурированных жидкостей.
3.Определить к какому типу (модели) относится изучаемая среда (ньютоновская, Бингама, Оствальда-де-Виле и т.д.)
4. Подобрать подходящее уравнение, описывающее ее поведение.
Пример выполнения
1. Получен следующий массив экспериментальных данных:
Напряжения сдвига τ, Па, при скоростях сдвига , с–1 |
||||||||||||
1,0 |
1,8 |
3,0 |
5,4 |
9,0 |
16,2 |
27,0 |
48,6 |
81,0 |
145,7 |
243,0 |
437,4 |
, с–1 |
2,5 |
3,2 |
4,8 |
5,7 |
4,9 |
14,7 |
23,5 |
41,5 |
67,7 |
123,7 |
206,3 |
371,2 |
τ, Па |
6,5 |
10,6 |
16,3 |
26,3 |
44,7 |
71,0 |
123,5 |
198,0 |
338,3 |
511,5 |
701,3 |
815,0 |
τ, Па |
2. Строим координатную сетку в координатах напряжение сдвига – градиент скорости деформации (τ – ) и наносим экспериментальные точки как представлено в примере на рис.6. Затем аппроксимируем полученные ряды точек в две кривые течения как показано на рис. 6.
Из курса математики известны три способа задания функциональных зависимостей: аналитический (уравнение кривой), табличный (таблица с данными) и графический. На практике часто приходится сталкиваться с задачей сглаживания экспериментальных данных – задачей аппроксимации. Основная задача аппроксимации – построение приближенной (аппроксимирующей) функции наиболее близко проходящей около данных точек. Аппроксимация – процесс подбора эмпирической функции φ(х) для установления из опыта функциональной зависимости y= φ(х)
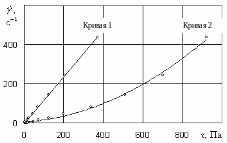
Рис. 6. Пример построения кривых течения
3. После построения кривых течения определяем к какому типу (модели) относится данная среда (см. рис. 5).
4. Находим уравнения, которыми описываются исследуемые среды и записываем их в общем виде.
Для рассмотренного примера (рис. 6) можно заключить, что кривая течения 1 является практически прямой линией проходящей через начало координат. В таком случае течение данного материала может быть описано уравнением Ньютона:
,
(8)
где
– динамическая (ньютоновская) вязкость,
Па
с.
Из характеристики кривой течения 2 видно, что течение жидкости можно описать степенным уравнением Оствальда-де-Виле для аномально-вязких жидкостей:
,
(9)
где
– консистентная переменная, Па
с;
– индекс
течения.
5. Далее необходимо определить коэффициенты реологических уравнений, которыми описывается течение заданных сред.
В уравнении 8 необходимо определить коэффициент динамической вязкости , для чего нужно замерить угол наклона кривой к оси абсцисс. Тангенс полученного угла наклона будет равен значению коэффициента динамической вязкости .
Пусть, например, получен угол наклона кривой к оси абсцисс 48о. Находит тангенс этого угла с помощью калькулятора и получаем ответ 1,1.
Для получения коэффициентов уравнения 9, необходимо прологарифмировать исходные данные рис. 6 (кривая 2) с помощью калькулятора. Получим табл.3.
Таблица 3. Прологарифмированные данные для построения кривой 2
, с–1 |
0,4 |
0,5 |
0,7 |
0,8 |
0,7 |
1,2 |
1,4 |
1,6 |
1,8 |
2,1 |
2,3 |
2,6 |
τ, Па |
0,8 |
1,0 |
1,2 |
1,4 |
1,7 |
1,9 |
2,1 |
2,3 |
2,5 |
2,7 |
2,8 |
2,9 |
По
результатам логарифмирования строим
логарифмическую кривую течения в
координатах lg
τ
– lg
(рис.7).
В результате логарифмирования получаем прямую линию, которая пересекается с осью ординат (значение коэффициента m). Значение коэффициента n находится как тангенс угла наклона к оси абсцисс. Например, тангенс угла в 42о равен 0,9.
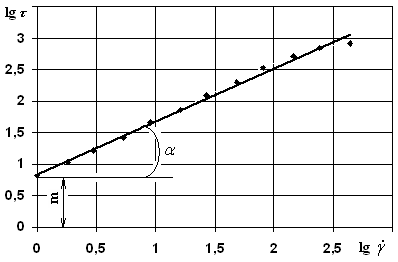
Рис. 6. Логарифмическая кривая течения
6.
После определения всех коэффициентов
записываем уравнения, которыми описывается
течение исследуемых сред, используя
найденные коэффициенты: для кривой 1
;
для кривой 2
Ответ. Для кривой 1: ; для кривой 2: .