Практическая часть
Таблица 3. Варианты с данными, полученными на ротационном вискозиметре
Вариант |
Напряжения
сдвига τ,
Па, при скоростях сдвига
|
|||||||||||
1,0 |
1,8 |
3,0 |
5,4 |
9,0 |
16,2 |
27,0 |
48,6 |
81,0 |
145,7 |
243,0 |
437,4 |
|
1 |
29,0 |
30,0 |
31,0 |
32,0 |
33,0 |
35,0 |
39,0 |
43,0 |
47,0 |
55,0 |
65,0 |
80,0 |
4,0 |
6,0 |
7,0 |
9,0 |
12,0 |
15,0 |
20,0 |
23,0 |
32,0 |
42,0 |
49,0 |
66,0 |
|
2 |
18,0 |
19,0 |
20,0 |
22,0 |
23,0 |
24,0 |
25,0 |
26,0 |
28,0 |
31,0 |
36,0 |
47,0 |
1,0 |
3,0 |
4,0 |
8,0 |
11,0 |
23,0 |
38,0 |
77,0 |
120,0 |
210,0 |
350,0 |
670,0 |
|
3 |
4,4 |
4,6 |
5,0 |
5,2 |
5,7 |
7,0 |
9,0 |
12,0 |
19,0 |
29,0 |
44,0 |
79,0 |
12,0 |
15,0 |
16,0 |
19,0 |
20,0 |
23,0 |
28,0 |
31,0 |
32,0 |
34,0 |
37,0 |
45,0 |
|
4 |
1,0 |
1,0 |
2,0 |
2,0 |
3,0 |
6,0 |
15,0 |
29,0 |
70,0 |
150,0 |
350,0 |
820,0 |
5,0 |
7,0 |
9,0 |
11,0 |
15,0 |
21,0 |
28,0 |
37,0 |
45,0 |
60,0 |
81,0 |
104,0 |
|
5 |
8,5 |
8,7 |
8,9 |
9,1 |
9,3 |
9,8 |
11,0 |
13,0 |
16,0 |
21,0 |
32,0 |
49,0 |
15,0 |
19,0 |
21,0 |
26,0 |
29,0 |
36,0 |
42,0 |
50,0 |
55,0 |
67,0 |
79,0 |
95,0 |
|
6 |
2,9 |
3,0 |
3,1 |
3,1 |
3,2 |
3,3 |
3,4 |
3,6 |
4,8 |
9,3 |
19,0 |
55,0 |
2,0 |
5,0 |
7,0 |
12,0 |
20,0 |
38,0 |
60,0 |
110,0 |
200,0 |
340,0 |
540,0 |
990,0 |
|
7 |
1,0 |
1,0 |
2,0 |
2,0 |
3,0 |
5,0 |
12,0 |
31,0 |
70,0 |
180,0 |
380,0 |
1000 |
12,0 |
17,0 |
23,0 |
39,0 |
50,0 |
78,0 |
100,0 |
160,0 |
200,0 |
300,0 |
450,0 |
640,0 |
|
8 |
24,0 |
30,0 |
35,0 |
43,0 |
52,0 |
59,0 |
72,0 |
87,0 |
100,0 |
110,0 |
130,0 |
180,0 |
3,3 |
3,4 |
3,4 |
3,5 |
3,5 |
3,6 |
3,8 |
4,1 |
4,5 |
5,5 |
7,1 |
9,7 |
|
9 |
8,8 |
8,9 |
9,0 |
9,0 |
9,2 |
9,5 |
9,7 |
12,0 |
15,0 |
23,0 |
43,0 |
97,0 |
0,0 |
1,0 |
1,0 |
2,0 |
2,0 |
5,0 |
11,0 |
32,0 |
70,0 |
160,0 |
390,0 |
950,0 |
|
10 |
3,3 |
3,3 |
3,4 |
3,4 |
3,5 |
3,6 |
4,1 |
5,3 |
8,5 |
17,0 |
38,0 |
96,0 |
5,0 |
6,0 |
8,0 |
11,0 |
13,0 |
18,0 |
24,0 |
29,0 |
31,0 |
37,0 |
45,0 |
61,0 |
|
11 |
20,3 |
21 |
21,7 |
22,4 |
23,1 |
24,5 |
27,3 |
30,1 |
32,9 |
38,5 |
45,5 |
56 |
2,8 |
4,2 |
4,9 |
6,3 |
8,4 |
10,5 |
14 |
16,1 |
22,4 |
29,4 |
34,3 |
46,2 |
|
12 |
12,6 |
13,3 |
14 |
15,4 |
16,1 |
16,8 |
17,5 |
18,2 |
19,6 |
21,7 |
25,2 |
32,9 |
0,7 |
2,1 |
2,8 |
5,6 |
7,7 |
16,1 |
26,6 |
53,9 |
84 |
147 |
245 |
469 |
|
13 |
3,08 |
3,22 |
3,5 |
3,64 |
3,99 |
4,9 |
6,3 |
8,4 |
13,3 |
20,3 |
30,8 |
55,3 |
8,4 |
10,5 |
11,2 |
13,3 |
14 |
16,1 |
19,6 |
21,7 |
22,4 |
23,8 |
25,9 |
31,5 |
|
14 |
0,7 |
0,7 |
1,4 |
1,4 |
2,1 |
4,2 |
10,5 |
20,3 |
49 |
105 |
245 |
574 |
3,5 |
4,9 |
6,3 |
7,7 |
10,5 |
14,7 |
19,6 |
25,9 |
31,5 |
42 |
56,7 |
72,8 |
|
15 |
5,95 |
6,09 |
6,23 |
6,37 |
6,51 |
6,86 |
7,7 |
9,1 |
11,2 |
14,7 |
22,4 |
34,3 |
10,5 |
13,3 |
14,7 |
18,2 |
20,3 |
25,2 |
29,4 |
35 |
38,5 |
46,9 |
55,3 |
66,5 |
|
16 |
2,03 |
2,1 |
2,17 |
2,17 |
2,24 |
2,31 |
2,38 |
2,52 |
3,36 |
6,51 |
13,3 |
38,5 |
1,4 |
3,5 |
4,9 |
8,4 |
14 |
26,6 |
42 |
77 |
140 |
238 |
378 |
693 |
|
17 |
0,7 |
0,7 |
1,4 |
1,4 |
2,1 |
3,5 |
8,4 |
21,7 |
49 |
126 |
266 |
700 |
8,4 |
11,9 |
16,1 |
27,3 |
35 |
54,6 |
70 |
112 |
140 |
210 |
315 |
448 |
|
18 |
16,8 |
21 |
24,5 |
30,1 |
36,4 |
41,3 |
50,4 |
60,9 |
70 |
77 |
91 |
126 |
2,31 |
2,38 |
2,38 |
2,45 |
2,45 |
2,52 |
2,66 |
2,87 |
3,15 |
3,85 |
4,97 |
6,79 |
|
19 |
14,21 |
14,7 |
15,19 |
15,68 |
16,17 |
17,15 |
19,11 |
21,07 |
23,03 |
26,95 |
31,85 |
39,2 |
1,96 |
2,94 |
3,43 |
4,41 |
5,88 |
7,35 |
9,8 |
11,27 |
15,68 |
20,58 |
24,01 |
32,34 |
|
20 |
8,82 |
9,31 |
9,8 |
10,78 |
11,27 |
11,76 |
12,25 |
12,74 |
13,72 |
15,19 |
17,64 |
23,03 |
0,49 |
1,47 |
1,96 |
3,92 |
5,39 |
11,27 |
18,62 |
37,73 |
58,8 |
102,9 |
171,5 |
328,3 |
|
,
с–1
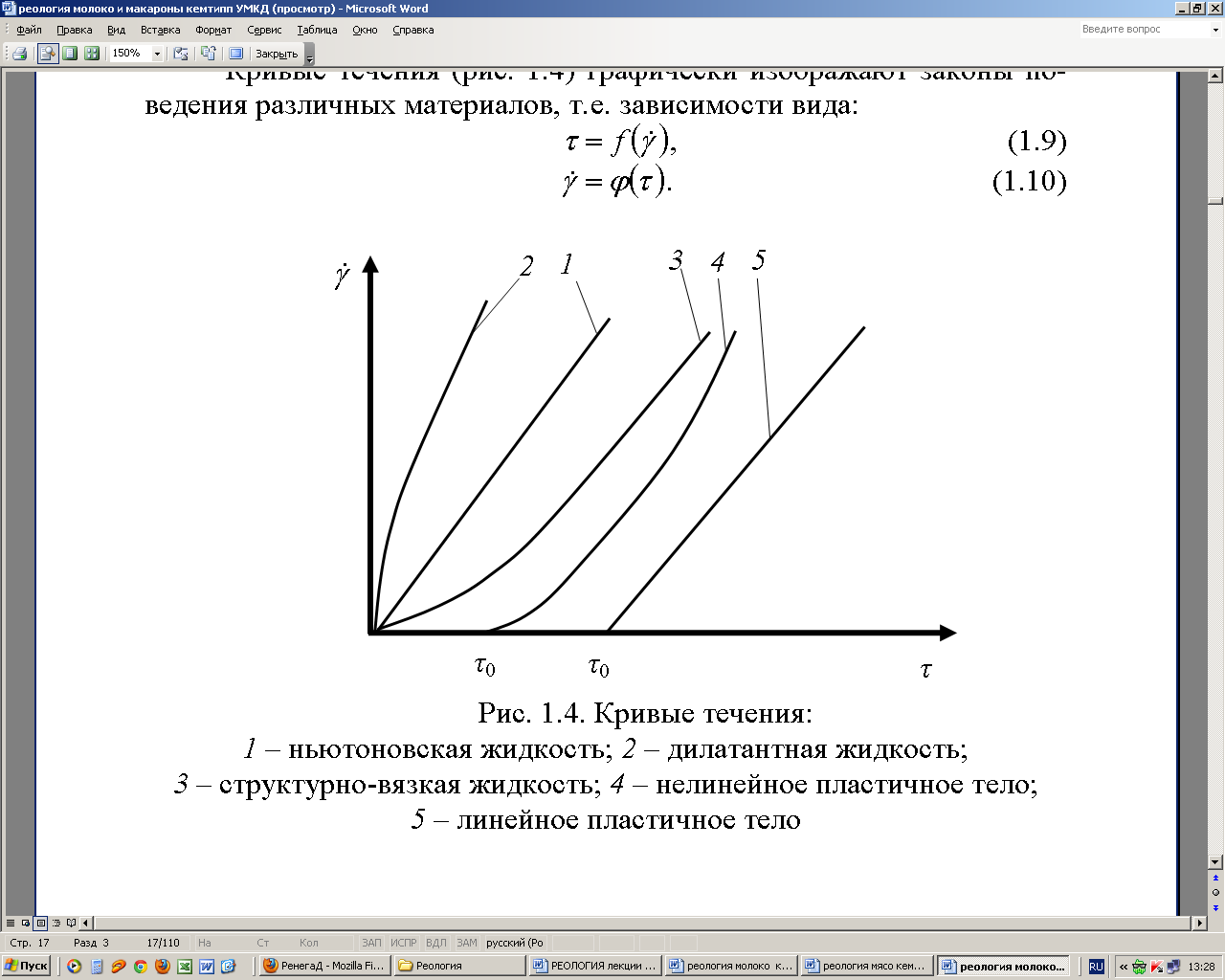
Возможные кривые течения пищевых материалов показаны на рис. 5. Кривые течения (реограммы) ньютоновских жидкостей представляют собой прямую линию 1, проходящую через начало координат. Для таких жидкостей применимо реологическое уравнение Ньютона (см. пример выполнения задания).
Все кривые течения (2-5), которые отклоняются от прямой линии, называют неньютоновскими (аномально-вязкими) жидкостями, т.е. у таких пищевых материалов вязкость изменяется от скорости деформирования. Такие жидкости описываются реологическим уравнением Оствальда-де-Виля (см. пример выполнения задания).
Кривая 2 характеризует дилатантное течение, характерное в основном для концентрированных дисперсных систем, при котором с увеличением скорости деформации наступает «затруднение сдвига», т.е. происходит повышение вязкости.
Кривая 3 описывает псевдопластическое течение, что характерно для «сдвигового размягчения» вследствие разрушения структуры с увеличением скорости деформации;
. |
Рис. 5. Кривые течения: 1 – ньютоновской жидкости; 2 – дилатантной жидкости; 3 – структурно-вязкая жидкость; 4 – нелинейного пластичного тела; 5 – линейного пластичного тела
|
Кривая 4 показывает нелинейное пластическое течение, характерное для большинства пластичных тел после достижения предельного напряжения сдвига τ0, реологическое уравнение Гершеля–Балкли описывает их поведение:
. (6)
где
- коэффициент, пропорциональный вязкости
при градиенте скорости, равном единице,
Па·сn;
n - индекс течения.
Линейная зависимость 5 характерна для бингамовских тел и соответствует идеальному пластичному течению, у которых после достижения предельного напряжения сдвига τ0 наблюдается пропорциональность между скоростью и напряжением сдвига. Такие материалы описываются уравнением Бингама:
, (7)
где ηпл – пластическая вязкость, Па·с.