2.3 Основные соотношения

2.3.1 Скольжение

При вращении с частотой сети f вектор магнитной индукции В пересекает короткозамкнутые витки ротора, в которых возникает ЭДС, вызывающая большие токи вследствие малого сопротивления витков ротора. Эти токи взаимодействуют с полем ротора, вызывая момент сил, стремящихся повернуть ротор вслед за полем. Токи максимальны, когда ротор неподвижен, равны нулю, если скорости вращения ротора и поля одинаковы. Из сказанного следует, что условием вращения ротора АД является его отставание от вращающегося магнитного поля. Отставание тем больше, чем больше момент нагрузки и характеризуется величиной называемой скольжением S.

S= = = , 2.2

где n_C , f_C и –скорость, частота и круговая частота вращения электромагнитного поля, синхронная скорость (f_C= , =2 f_C),

n, f и -- скорость, частота и круговая частота вращения ротора.

2.3.2 Скорость вращения электромагнитного поля определяется следующим образом. Если число пар полюсов трехфазного АД равно единице, то вектор магнитной индукции В, вращаясь с частотой сети f, совершает f оборотов за одну секунду (рис. 2.5а). В документации на АД величины задаются в оборотах в минуту. Поэтому

n_C=60f. 2.3

На рис. 2.5а обмотка каждой фазы показана в виде одного витка, обмотки соединены звездой. На рис. 2.5б обмотки показаны условно в виде катушек, расположенных под углом 120⁰ друг к другу.

Если число пар полюсов два (рис2.5в), период оканчивается на половине окружности, т.е. синхронная скорость в два раза ниже n_C= , при трех парах полюсов n_C= .

В общем случае

n_C= 2.4

где p—число пар полюсов.

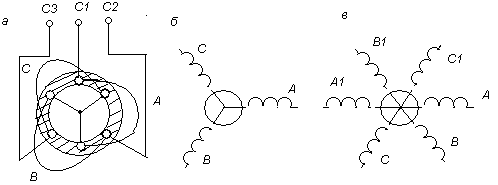
Рисунок 2.5 К вопросу о синхронной скорости.

2.3.3 Электродвижущие силы, наводимые в обмотках ад.

Трехфазный АД можно рассматривать как трансформатор, первичными обмотками которого являются обмотки статора, вторичными—ротора. Магнитная цепь АД проходит через сердечник статора в ротор и обратно (отличием от трансформатора является наличие воздушного зазора между ротором и статором). Как и в трансформаторе по магнитной цепи проходит основной магнитный поток Ф, сцепленный с обмотками статора и ротора. Точно так же существуют два потока рассеяния: поток рассеяния обмотки ротора и поток рассеяния обмотки статора. Напряжение, поданное на обмотку статора , преодолевает ЭДС (- ) первичной обмотки (знак – говорит о противоположной направленности ЭДС), падает на активном сопротивлении r₁ и индуктивном сопротивлении х₁ первичной обмотки, что можно выразить соотношением:

=(- ) + j r₁+ j x₁ 2.5

которое является уравнением напряжений обмотки статора.

Если ротор не вращается (заторможен или в момент пуска), АД представляет собой трансформатор, с замкнутой накоротко вторичной обмоткой. В этой обмотке по известному соотношению возникает ЭДС Е₂=4,44f_CФw₂k,

где w₂k --число витков ротора, с учетом отличия его конструкции от конструкции трансформатора; к—обмоточный коэффициент обмотки ротора, а f_C частота сети.

При вращении ротора в его обмотке возникает ЭДС , которую можно выразить тем же соотношением:

= 4,44 f_SФw₂k, 2.6

где f_S—частота скольжения, равная разности частот поля f_C и частоты вращения ротора f : f_S=(f_C -f); с этой частотой меняется магнитное поле ротора.

= 4,44 f_SФw₂k,=4,44(f_C – f)Фw₂k=4,44(f_C – f)Фw₂k =

=4,44f_C Фw₂k =4,44f_C Фw₂k S= Е₂S, 2.7

где S –скольжение,

Е₂=4,44f_C Фw₂k—ЭДС , наведенная в обмотке ротора при скольжении S=1, т.е. при неподвижном роторе.

Из 2.7 можно сделать вывод о том, что чем больше скольжение, тем больше ЭДС ротора. Максимальной ЭДС будет при неподвижном роторе (S=1). В этом случае = Е_2..

ЭДС создает в роторе ток частоты f_S, что соответствует круговой частоте скольжения _S = _С - . Этот ток создает магнитный поток ротора , на создание которого затрачивается часть ЭДС _Р. Эта ЭДС называется ЭДС рассеяния, а магнитный поток –потоком рассеяния. Вторая часть ЭДС затрачивается на падение напряжения на сопротивлении ротора r₂ r₂.

= _Р + r₂. 2.8

Магнитному потоку рассеяния соответствует индуктивное сопротивление в цепи ротора х₂¹:

х₂¹ = _S L 2.9

где _S = _С - -круговая частота скольжения (сравни с 2.6).

х₂¹ = _S L=( _С - )L = L = S L =х₂S,

где х₂= L— индуктивное сопротивление цепи, создающей магнитный поток рассеяния при скольжении S=1 (при скорости ротора =0).

ЭДС рассеяния ротора в комплексной форме

_Р= j х₂¹= j x₂S, 2.10

Из равенства 2.8 после подстановки значений входящих в него величин (из соотношений 2.7 и 2.10) получается

S - j x₂S = r₂ 2.11

В результате деления на S получается уравнение напряжений для ротора АД:

- j x₂ - =0 2.12

Выражение 2.12 позволяет сделать интересный вывод: чем больше скольжение, тем меньше влияние активного сопротивления ротора. Это значит, что при пуске двигателя большое сопротивление обмоток ротора мало влияет на характеристики пуска. В то же время введение в цепь ротора на время пуска большого сопротивления позволяет уменьшить пусковые токи.