5. Модели взаимодействия

В двухпутевых моделях, описанных в 2.4. предполагалось, что построенные уравнения не содержат взаимодействия между b_i- и s_j-параметрами, т.е. графики и представляют собой параллельные линии. В практике же нередко встречаются ситуации, когда подобное взаимодействие существует. Например, в молочном скотоводстве для улучшения племенных качеств красного степного скота используются две улучшающие породы – англерская и красная датская. Естественно, что повышение кровности животных по каждой из них приводит к неадекватным результатам. В таком случае отмечают, что существует взаимодействие типа «порода-кровность». Аналогичным образом можно константировать взаимодействие типа «генотип-среда», «порода-пол» и т.п.

При наличии связи между независимыми параметрами используются модели взаимодействия, которые можно представить в виде:

2. y_ijk – наблюдаемая переменная;

µ- популяционное значение;

b_i – фиксированный независимый параметр (i=1,2, …, p);

s_j – фиксированный независимый параметр (i=1 ,2, …,q);

bs_ij – эффект взаимодействия, специфичный для i-ого b-параметра и j-ого s-параметра;

e_ijk – остаточный случайный эффект, связанный с K-наблюдением ~ .

В этом случае математическое ожидание Е(у_ijk) представляет не просто сумму значений параметров «b» и «s», а включает и константу взаимодействия .

Анализ и интерпретация результатов интеракционных моделей представляются более сложными, чем в случае обычных двухпутевых классификаций и в значительной степени зависят от структуры входных данных:

1. Все интеракционные сочетания представлены в исходном массиве.

2. Набор данных с «потерянными» эффектами взаимодействий.

1. Модели максимального заполнения

Моделями максимального заполнения в процедурах взаимодействия называются уравнения, описывающие входные данные таким образом, что существует, по крайней мере, одно наблюдение j-ого s-эффекта в любом уровне b_i. Другими словами в исходном массиве, отсутствуют нулевые наблюдения в каком-либо сочетании bs_ij.

Как и обычно, описание решения проводится согласно:

.

Элементы матриц Х′Х и Х′у, а также вектора решений в скалярной форме могут иметь вид:

.

Поскольку ранг матрицы Х′Х будет равен числу градаций взаимодействий (т.е. ), то простейшее решение для определения интеракционных параметров можно получить путем исключения параметров µ, r,s (т.е. µ=r=s=0). Тогда инверсию матрицы Х′Х можно представить в виде:

.

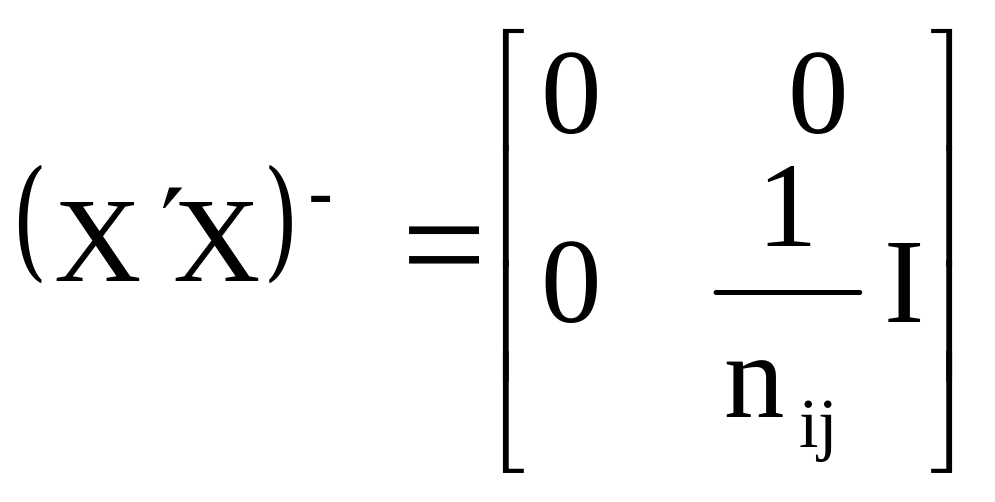Решение уравнений упрощается до:

.

Как обычно, для получения остаточной вариансы необходимо вычислить сумму квадратов:

;

;

.

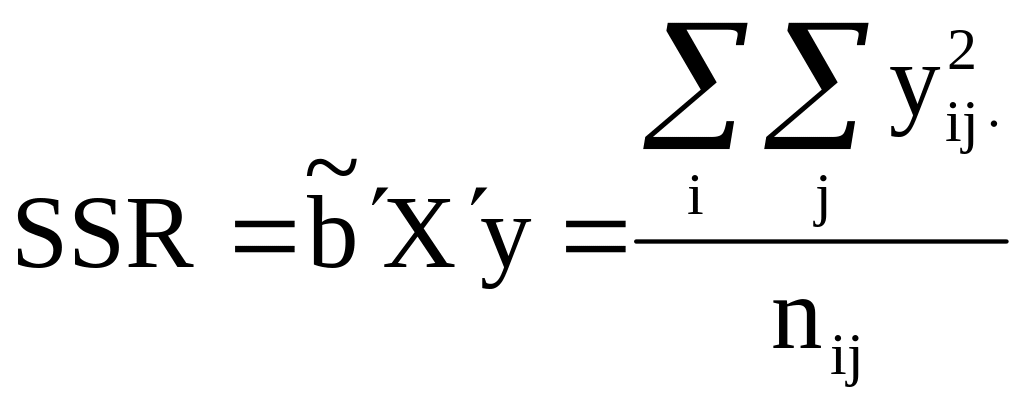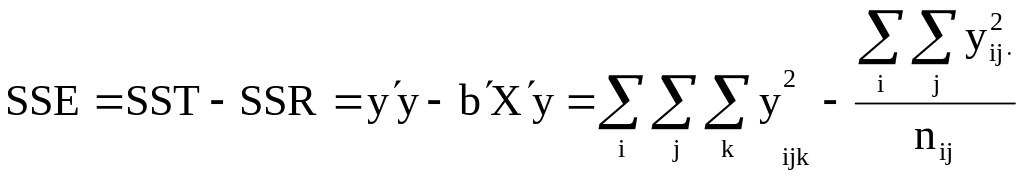В этом случае оценка вариансы ошибки описывается согласно:

.

Оценочные функции можно построить следующим образом.

1. Интеракционные эффекты оцениваются как:

;

.

2. Оценить разницу между b_i и b_i′,и а также s_i и s_i′ непосредственно невозможно, поскольку в исходной модели присутствуют эффекты взаимодействия. Вместе с тем эта разница может быть описана:

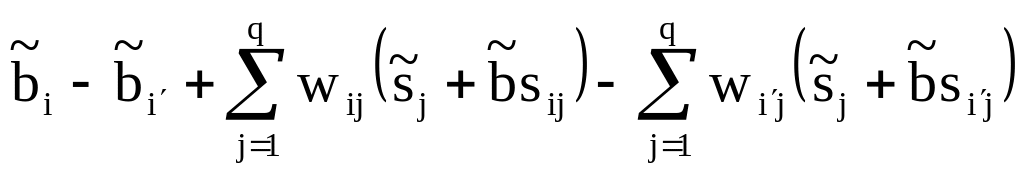1. , где i≠i′;

;

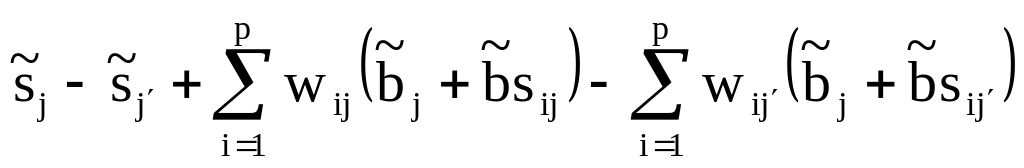2. , где j≠j′;

Очевидно, что разница, описываемая в пунктах а и b, оценивается в пределах общего s_j-параметра (n.а) и общего b_i-эффекта (n.b).

Варианса разницы в этих случаях определяется как:

;

.

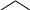3. Оценку различий между интеракционными эффектами можно провести согласно общей формулы:

;

.

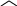Анализу вариансы, как и в предыдущих типах моделей, предшествует вычисление сумм квадратов полной и редуцированных моделей:

для полной модели ;

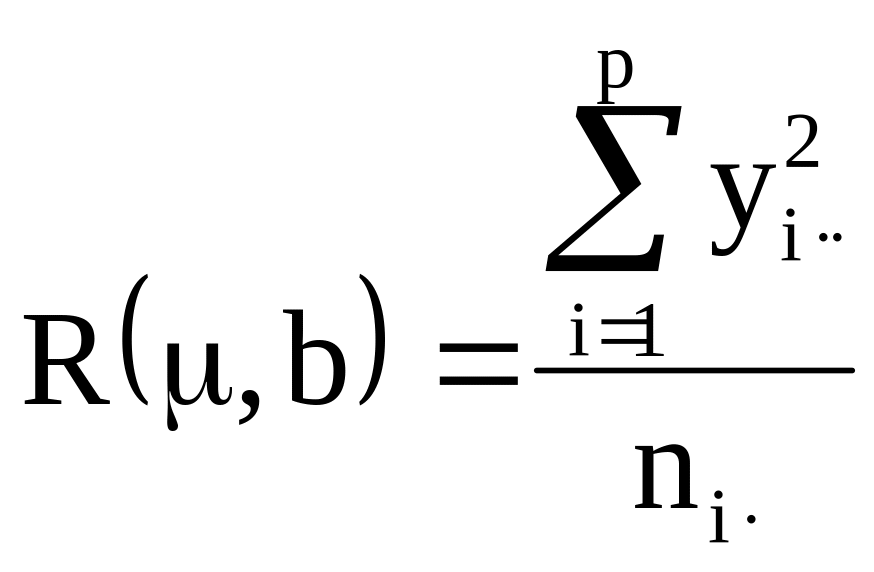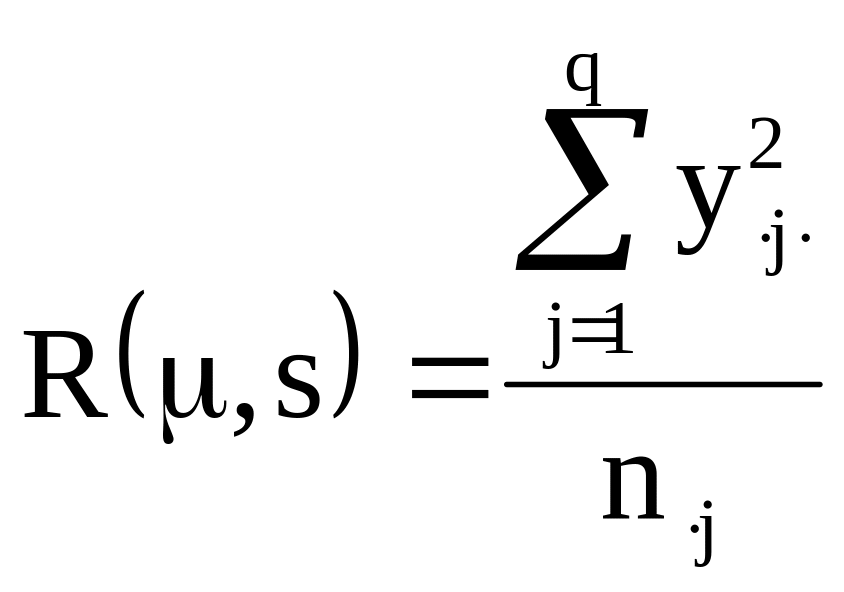для редуцированной модели ;

для редуцированной модели ;

для редуцированной модели ;

для редуцированной модели .

Из приведенных соотношений легко получить остальные суммы квадратов:

;

;

;

;

;

.

Итоговые результаты могут быть представлены в табл. 2.7. – 2.9.

Таблица 2.7.

ANOVA

Источник	df	Суммы квадратов	Средний квадрат	F-тест
Общепопуляционное значение	1
b,s,bs|µ	pq-1
Остаточный эффект	N-pq			—

Тaблица. 2.7. оценивает значимость модели, описывающей общую вариансу путём вычисления µ, а затем b-, s- и bs–эффектов после µ.

Таблица 2.8.

ANOVA

Источник	df	Суммы квадратов	Средний квадрат	F-тест
Общепопуляционное значение	1
b|µ	p-1
s|µ,b	q-1
bs|µ,b,s	pq-p-q+1
Остаточный эффект	N-pq			—

Значения таблицы 2.8. подразделяются на последовательное вычисление µ, затем b после µ, s после µ, b, bs после µ, b, s.

Таблица 2.9.

ANOVA

Источник	df	Суммы квадратов	Средний квадрат	F-тест
Общепопуляционное значение	1
b|µ,s	p-1
s|µ,b	q-1
bs|µ,b,s	pq-p-q+1
Остаточный эффект	N-pq			—

Тип анализа таблицы 2.9. может подразделять последовательное вычисление каждого из включённых в общую модель параметра после общепопуляционной средней и оставшихся эффектов.

Для проверки различного рода гипотез используется общая формула:

,

где .

Уравнение для вычисления числителя будет истинным только в случае, когда можно оценить (т.е. оно является оценочной функцией).

Конкретные формы гипотетических функций могут быть предоставлены аналогично видам оценочных уравнений. Так, например, различия между b_i- и b_i′-параметрами для общего s_j-эффекта оцениваются согласно проверке:

.

Тогда:

,

.

Согласно последовательности типов оценочных функций, приведенных выше, гипотетические проверки соответственно имеют вид:

1. представляет собой числитель сумм квадратов для проверки:

эквивалентно для всех i.

Соответственно проверяет

эквивалентно для всех j.

2. представляет собой числитель сумм квадратов для проверки:

.

3. представляет собой числитель сумм квадратов для проверки:

   H :

   Любой набор из (pq-p-q+1) линейно-независимых функций различий 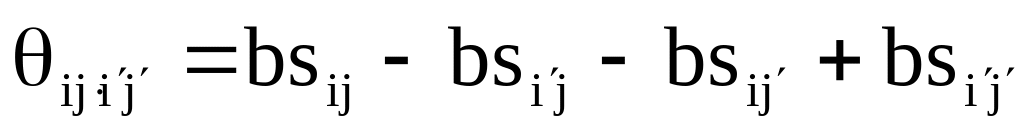, где такие функции представляют оценку θ или оцениваемых сумм или разностей функции θ.

   =0.

4. Числитель сумм квадратов может быть построен для проверки.'

Н : эквивалентность для всех i=1, 2, …, р.

Она равнозначна проверке эквивалентности наименьших квадратных значений для параметра «b».

Соответственно проверка эквивалентности наименьших квадратичных значений для параметра «s»:

Н : эквивалентность для всех j=1, 2, …, q.

Тогда таблица анализа вариансы будет иметь вид:

Таблица 2.10.

ANOVA

Источник	df	Суммы квадратов	Средний квадрат	F-тест
Общепопуляционное значение	1
b-параметр	p-1
s-параметр	q-1
Взаимодействие	pq-p-q+1
Остаточный эффект	N-pq			—

Вычисление сумм квадратов относительно b- и s-параметров необходимо проводить последовательным сравнением пар значений по всем градациям i и j.

Пример.

Исходные данные, определяющие влияние рациона кормления и генетические эффекты отца на прирост живой массы, сгруппированы в двух таблицах: