2. Двухпутевая гнездовая классификация

В практике селекционной работы нередко встречаются ситуации, когда на результирующий параметр влияют ряд факторов, упорядоченно размещенных один в другом. Такого рода уравнения, в отличие от перекрестных моделей, носят название гнездовых или иерархических классификаций.

Общая модель двухпутевой гнездовой классификации может быть представлена в виде:

,

22. y_ijk – наблюдаемая (результирующая) переменная;

µ – популяционное значение (константа);

t_i – первый независимый эффект, представленный как фиксированный (i=1,2, …, p);

b_ij – второй независимый фиксированный эффект, размещенный внутри t_i (j=1,2, …, q);

е_ijk – эффект k-ого наблюдения внутри j-ого b-эффекта, который в свою очередь не выходит за пределы i-ого t-эффекта;

е_ijk – представляет как случайный эффект ~ .

В матричной форме исходное уравнение переписывается как:

.

Приводя уравнение к нормальному виду, получаем:

.

Отсюда решение нормализованного уравнения:

.

В данной модели матрица имеет неполный ранг, поэтому используется обобщенная инверсия. Ранг матрицы складывается из суммы: 1 для µ, (р-1) для t-эффекта, (q-p) для b-эффекта, который иерархически распределен внутри t-эффекта:

.

Тогда простейшее решение для обобщенной инверсии можно получить, положив . Заметим, что в этой ситуации решения представляют собой простые субклассовые значения для каждого b-параметра.

Оценка ошибочной вариансы вычисляется в следующей последовательности:

1. .

2. .

3. .

4. .

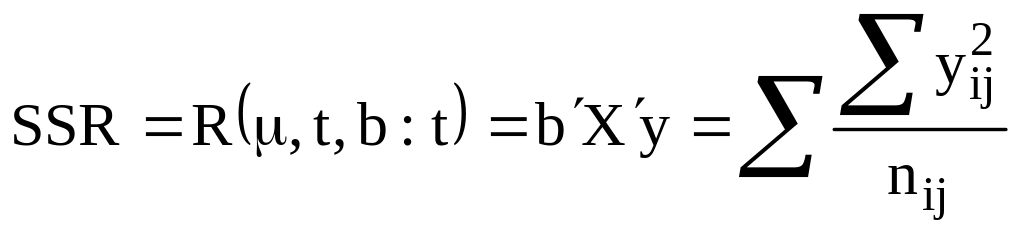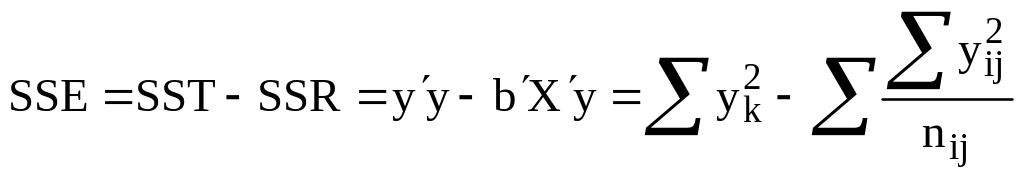В случае иерархической двухпутевой классификации могут быть использованы следующие типы оценочных функций:

1. ;

.

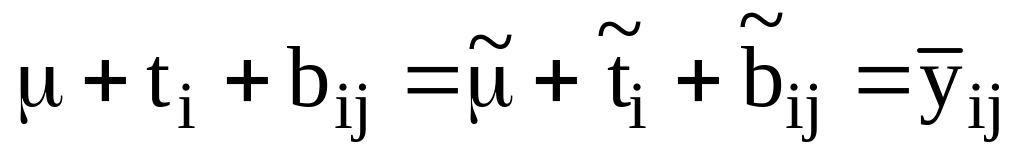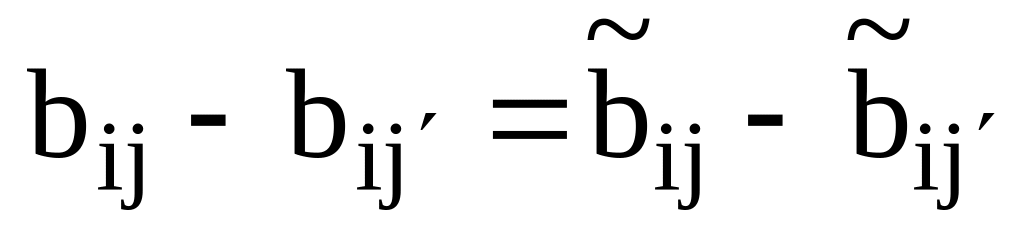
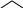2. для ;

.

3. 

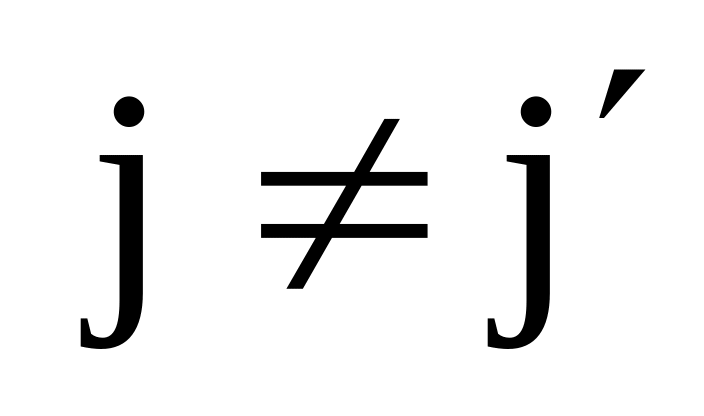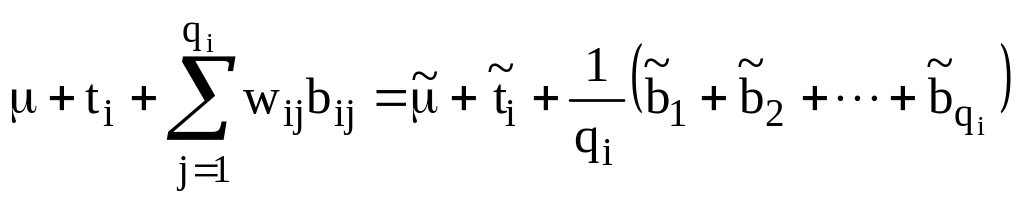
   1. q_i – число уровней b_ij в t_i-параметре.

Это выражение представляет собой наименьшее квадратичное значение для t-параметра.

4. Для гнездовой двухпутевой модели разница 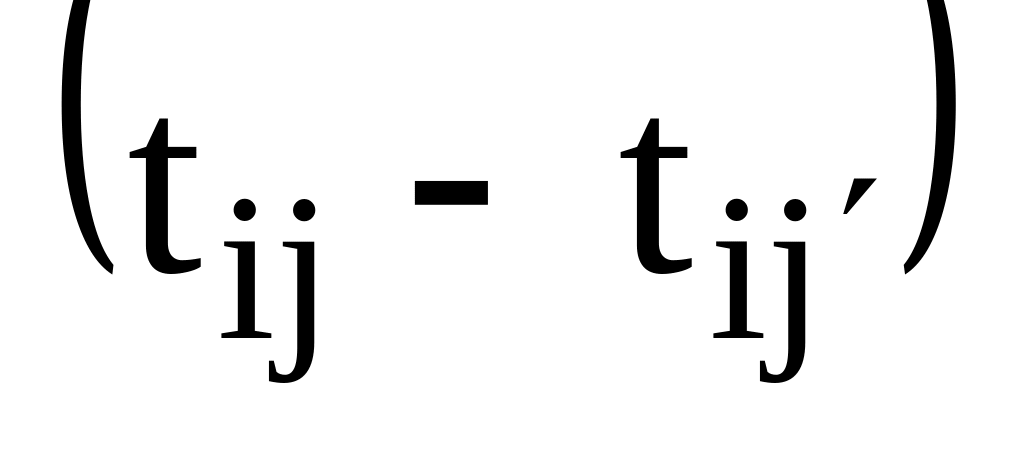не может быть оценена напрямую. Вместе с тем оценочную функцию разницы двух t-параметров можно определить согласно:

для

Общая формула оценки вариансы может быть представлена в виде:

.

Для определения, объясняет ли модель значимость вариации в у-переменной, формируется таблица анализа вариансы. Построение данной таблицы осуществляется в следующей последовательности:

1. Вычисление сумм квадратов:

;

;

;

;

.

2. Построение таблицы в виде:

Таблица 2.4.

ANOVA

Источник	df	Суммы квадратов	Средний квадрат	F-тест
Популяционное значение	1
Модель после µ	q–1
Остаточный эффект	N–q			—

Данная таблица анализирует адекватность полной модели (т.е. с включением как t- так и b-параметров) вариации в исходных данных, без проверки значимости отдельных независимых параметров, включенных в модель, т.е. t и b:t.

Разделить влияние отдельных параметров можно путем использования однопутевой классификации, игнорируя b-эффекты:

.

Под эту модель получаем:

;

.

Тогда, используя редуцированные суммы квадратов полной модели и однопутевой классификации, получаем:

.

Таким образом, редуцированная сумма квадратов из таблицы 2.4. может быть представлена как сумма:

,

и таблица анализа вариансы преобразуется в более информативный вид:

Таблица 2.5.

ANOVA

Источник	df	Суммы квадратов	Средний квадрат	F-тест
Популяционное значение (µ)	1
t после µ	p-1
(b:t) после µ	q–p
Остаточный эффект	N–q			—

В двухпутевой гнездовой классификации наиболее часто встречаются проверки эквивалентности всех b-параметров внутри t-уровня, а также t-уровней между собой.

Для проверки первой гипотезы необходимо построить матрицу K′, которая содержит парные позитивные и негативные единичные значения в b-параметре для каждой градации t-уровня. Проверка осуществляется согласно общему уравнению:

, где .

Проверка эквивалентности всех b-параметров внутри t-уровня равносильна проверке значимости в таблице анализа вариансы.

Вторую гипотезу невозможно проверить непосредственно, поскольку, как уже отмечалось, для не может быть оценено.

Гипотетическое уравнение можно построить как:

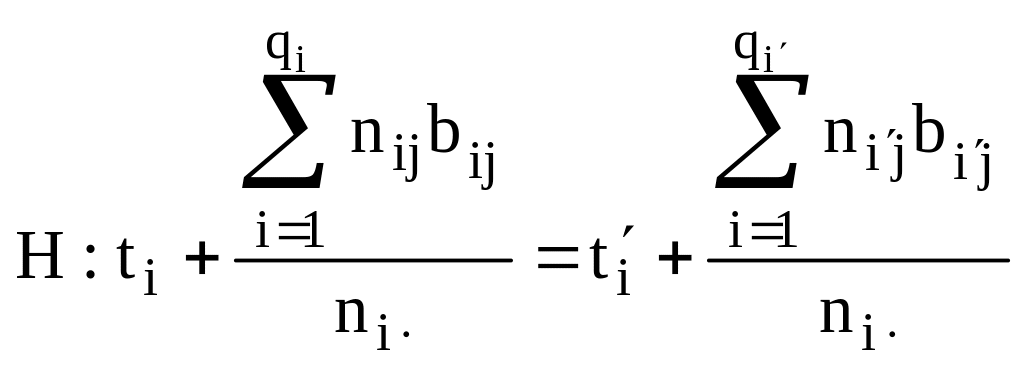для .

В такой ситуации матрица K′ может быть представлена как совокупность двух матриц, первая из которых составляет пары из 1 и (-1) для попарного сравнения уровней t, а вторая – средневзвешенное количество наблюдений b-параметра внутри «идентифицированных» уровней t-эффектов.

Тогда окончательное уравнение проверки будет:

.

Последний результат абсолютно эквивалентен проверке значимости в таблице анализа вариансы.

Пример.

Предположим, что имеются наблюдения прироста живой массы 12 животных пяти пород, относящихся к двум биологическим типам.

Исходные данные сведены в следующую таблицу:

Биологический тип	Порода	Прирост живо массы	Итого	Число наблюдений	Средняя величина
I	C	0,6	0,6	1	0,6
	M	0,9; 1,1; 0,1	3,0	3	1,0
			3,6	4	0,9
II	A	0,9; 1,1	2,0	2	1,0
	H	0,7; 0,3; 0,2; 0,4	1,6	4	0,4
	S	0,4; 0,8	1,2	2	0,6
			4,8	8	0,6
			8,4	12	0,7

Требуется оценить эффекты биологических типов и пород, а также проверить существование значимых различий между эффектами биологических типов и пород.

Исходный набор данных и поставленная цель исследований подразумевают использование двухпутевой гнездовой классификации, уравнение которой имеет следующий вид:

,

1. y_ijk – прирост живой массы k-го животного;

µ – популяционная константа;

t_i – фиксированный эффект i-го биологического типа (i=1, 2);

b_ij – фиксированный эффект j-ой породы внутри i-го биологического типа (j=1, 2 для i=1; j=1, 2, 3 для i=2);

e_ijk – рэндомизированная ошибка ~ .

Нормализованный вид системы уравнений можно выразить как:

Поскольку ранг матрицы , то решение уравнений можно представить в виде:

.

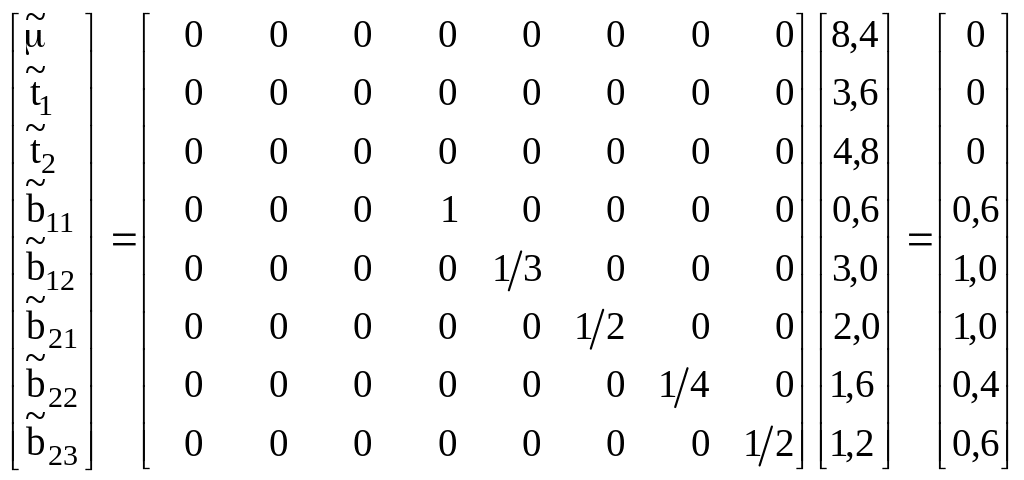Заметим, что в данном случае решения – это просто средние величины субклассов для каждой из пород.

Для описания остаточной вариансы необходимо вычислить:

;

;

.

Тогда:

.

Оценочные функции для гнездовой двухпутевой классификации могут быть представлены как:

1. .

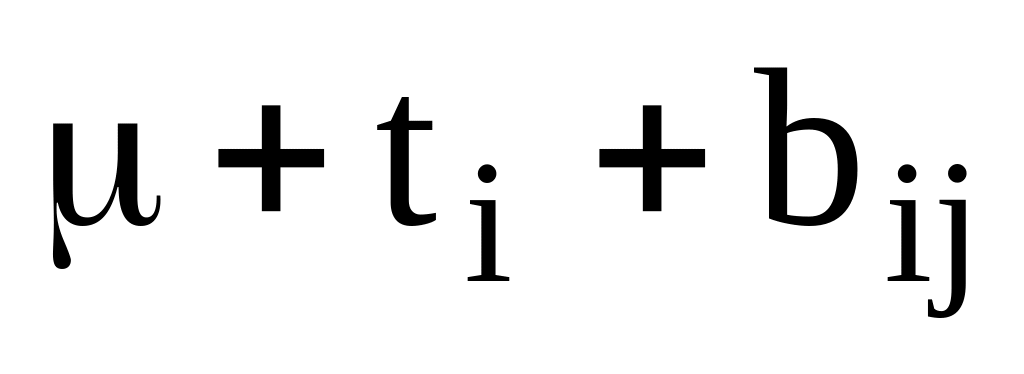Например,

;

.

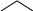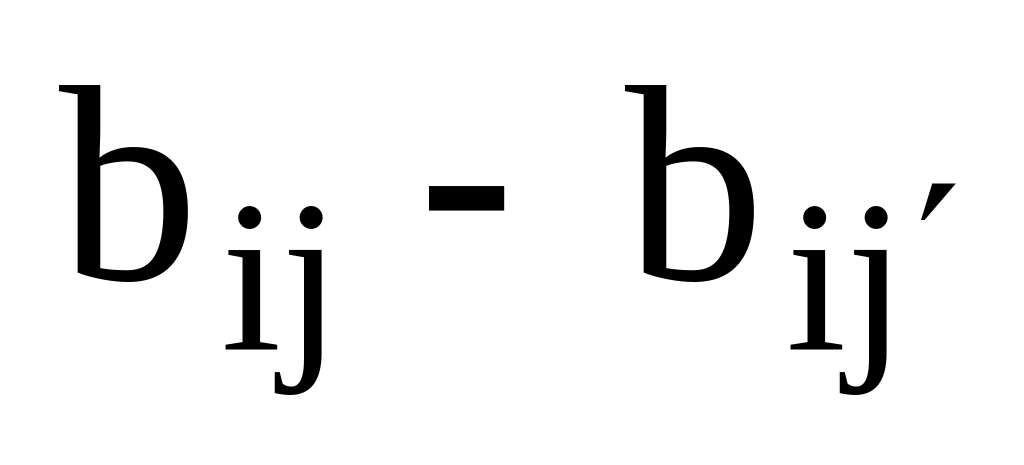2. для .

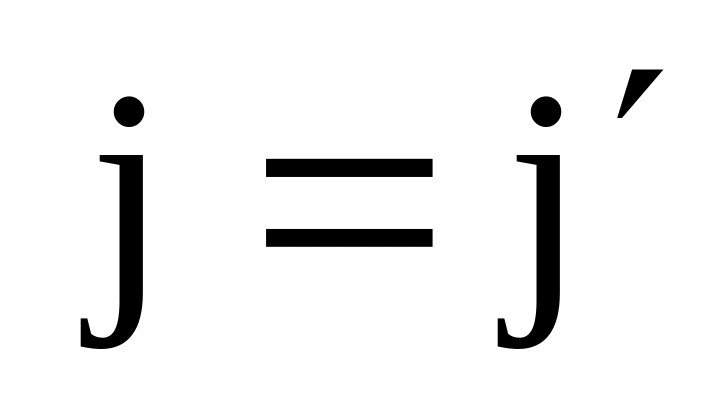Н апример, различия между С и М: 6 ;

..

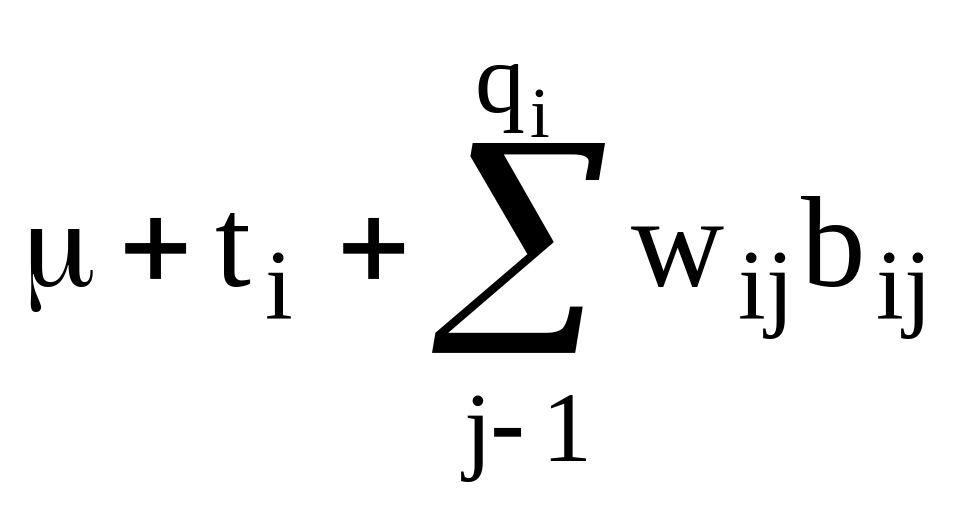3. (q_i – число уровней «b_ij» в t_i ).

Например,

.

4. .

Например,

Вариансу этого выражения можно оценить в цифровом выражении:

.

Вариансный анализ начинается с вычисления и .

Таблица анализа вариансы:

Источник	df	Суммы квадратов	Средний квадрат	F-тест
Константа	1		5,88	158,5**
Модель (после константы)	4		0,21	5,7*
Остаток	7		0,0371	—

Таким образом, выбранная модель учитывает значимую вариацию в приросте живой массы.

Вместе с тем данная таблица не разделяет влияние эффектов в модели. Это достигается за счет использования однопутевой классификации:

Под эту модель получаем:

;

.

Из полной модели следует:

.

Тогда таблица имеет вид:

Таблица 2.6.

ANOVA

Источник	df	Суммы квадратов	Средний квадрат	F-тест
Популяционное значение (µ)	1		5,88	158,5**
t|µ	1		0,24	6,5*
(b:t|µ,t)	3		0,20	5,4*
Остаток	7		0,0371	—

Это означает, что и биологический тип, и порода значимо влияют на вариацию в приросте живой массы.

Для проверки гипотезы эквивалентности всех уровней «b» внутри t_i матрица K′ приобретает вид:

.

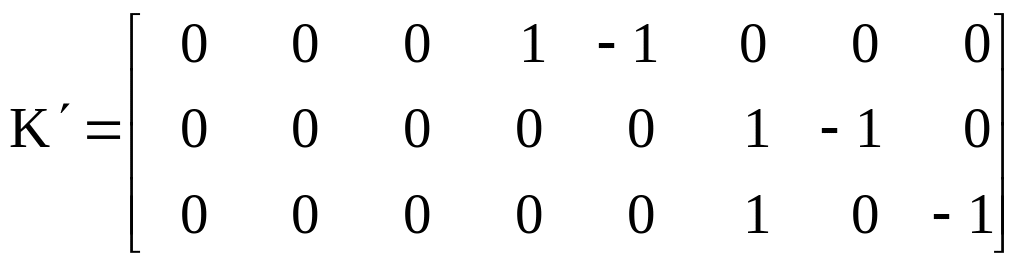Тогда:

;

;

;

.

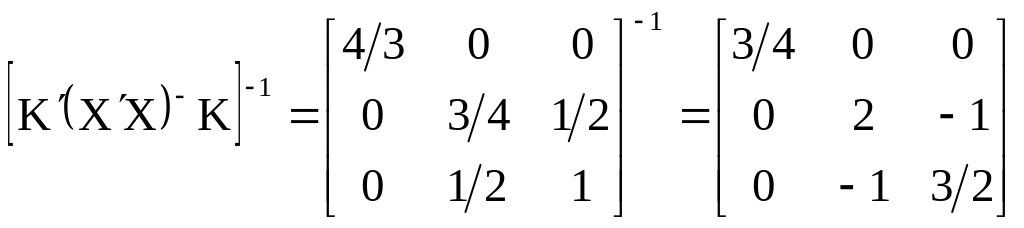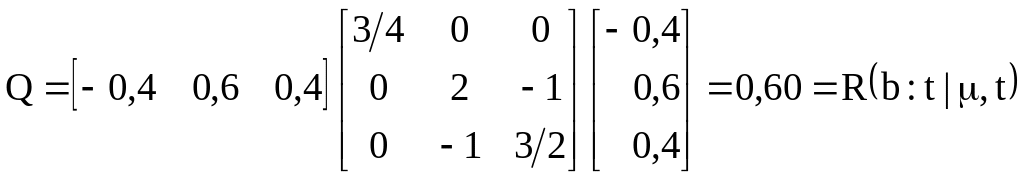Проверку эквивалентности влияния t-уровней на вариацию в приросте живой массы можно выполнить двумя способами:

• используя средневзвешенные значения;

• используя среднеарифметические значения коэффициентов при показателе «b».

В первом случае проверяется гипотеза:

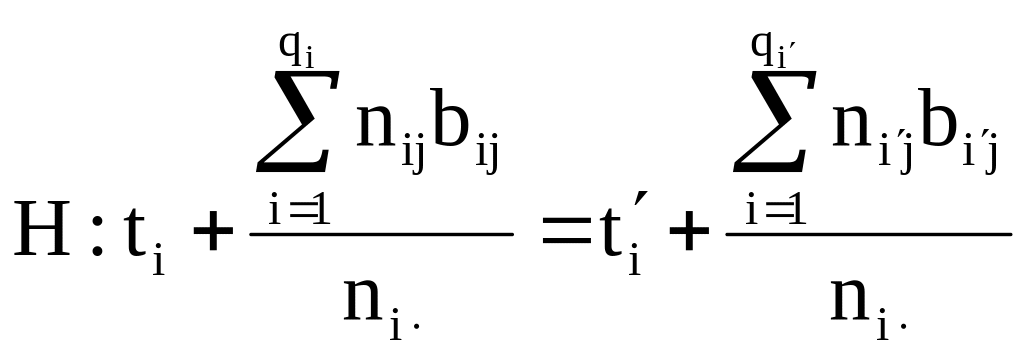
Под эту гипотезу:

;

;

;

;

– гипотеза отвергается.

Во втором случае гипотеза имеет вид:

.

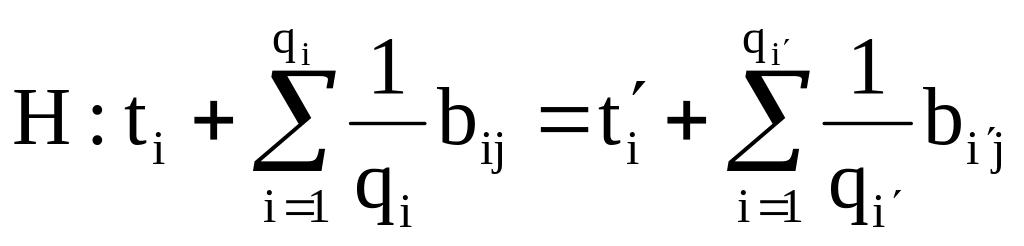Тогда:

;

;

;

;

– гипотеза принимается.