3. Однопутевая классификация

Под классификационными моделями (классификациями) понимаются модели, которые в качестве независимых параметров (аргументов) используют качественные или «квантированные» эффекты. К таким эффектам, например, могут быть отнесены: порода животного, набор генотипов, группировка типа «опыт-контроль», в ряде задач – группировка по уровню продуктивности стад или матерей оцениваемых выборок животных, дискретные категории племенной ценности отцов и пр.

Под однопутевой моделью подразумевается уравнение с одной независимой переменной:

,

11. y_ij – наблюдаемая переменная;

µ – константа или популяционная средняя;

b_i – эффект независимого параметра (фиксированный);

е_ij – рэндомизированный эффект ошибки, связанный с ij-ым наблюдением ~ (0, );

i – число градаций «b-эффекта»;

j – число наблюдений внутри каждой градации независимого параметра.

В матричной форме однопутевая модель может быть переписана:

для .

Тогда решение для «b» следующее:

,

12. (Х′Х)^– представляет собой обобщенную инверсию от матрицы

.

(Х′у) – вектор вида

.

В данной ситуации решение для b-параметра не является уникальным, поскольку рант матрицы Х′Х равен 1, т.е. матрица имеет неполный рант, и поэтому существует множество вариантов её инверсии. Однако, несмотря на «неуникальность» представления инверсных матриц, все решения имеют общие свойства:

1. .

Необходимо отметить, что математическое ожидание от « » не является оценкой b-параметра, а составляет лишь частное решение. Соответствие оценки и частных решений возможно только в случае, когда матрица Х′Х имеет полный ранг (т.е. все уравнения в указанной матрице линейно независимы).

2. .

3. .

Очевидно, что Х(Х′Х)^–Х′ представляет собой инвариант (Х′Х)^–, поэтому оценка будет уникальной, независимо от того, какая инверсия от (Х′Х) использована.

4. .

Заметим, что суммы квадратов ошибок (SSE) вычисляются аналогично случаю с матрицей полного ранга и не зависят от представления (Х′Х)^–.

5. Оценка ошибочной вариансы определяется как:

,

13. r(Х) – ранг матрицы Х′Х.

Таким образом, решение нормального уравнения является просто решением, а не оценкой b-параметров. Значение « » зависит от использованной структуры матрицы (Х′Х)^–. Оценка параметров «b» и их линейных комбинаций осуществляется при помощи так называемых оценочных функций, которые, в свою очередь, обладают следующими свойствами:

1. Ожидаемое значение любого наблюдения может быть оценено, т.е. , , … , могут быть оценены.

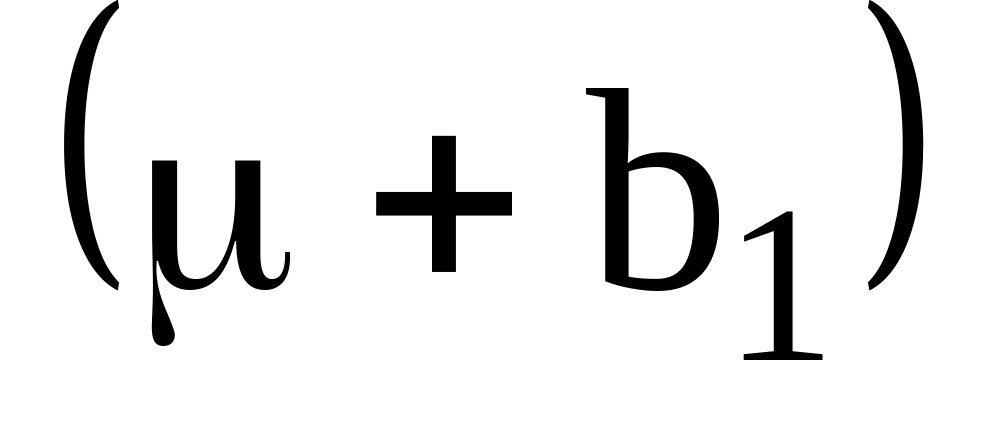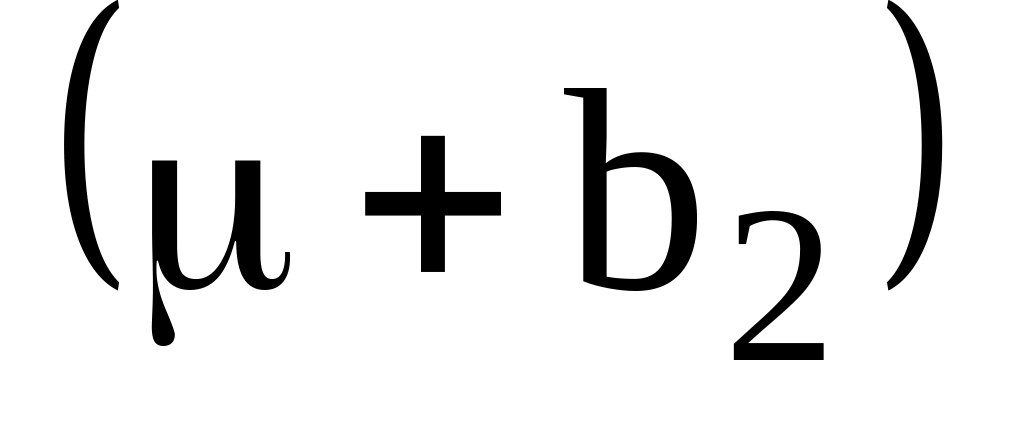2. Линейные комбинации оценочных функций могут быть оценены. Например, поскольку и оцениваемы, то и 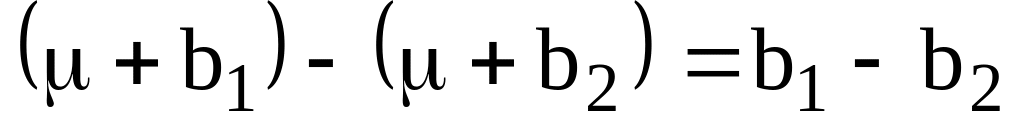может быть оценена.

3. Если K′b оцениваема, где K′ представляет собой линейную функцию от b-параметра, то К′b представляет собой инвариант для , независимо от того, какое решение для « » получено (т.е. независимо от формы представления инверсии матрицы Х′Х).

4. Любая линейная функция Хb оцениваема.

5. Если ранг матрицы Х′Х равен «r», то существует и «r» независимых оценочных функций.

6. Если K′(Х′Х)^–Х′Х=K′, тогда K′b – оцениваема.

Варианса от К'Ь может быть оценена как

,

и оценка вариансы от ( ) может быть получена путем подстановки вместо .

Следующий шаг в расчёте однопутевой классификационной модели – этап проверки гипотез.

Уравнение линейной гипотезы в общем виде записывается следующим образом:

,

14. K′ – матрица или набор линейных функций b-параметров, т.е. если – оцениваема, то для i=1, 2, …, S;

m – константа (в большинстве случаев m=0).

Сумма квадратов для проверки гипотезы

,

и под нулевую гипотезу необходимо проверить соотношение

~ ,

где F(S, N-r) – табличное значение критерия Фишера для (S, N-r) – числа степеней свободы.

В случае, когда m=0, вычисление гипотетического уравнения упрощается до следующего вида:

.

Анализ вариансы начинается с определения частных сумм квадратов:

;

;

;

;

.

В традиционной форме итоговая таблица анализа вариансы может быть представлена в следующем виде:

Таблица 2.1.

ANOVA

Источник	df	Суммы квадратов	Средний квадрат	F-соотношение
Модель	r
Свободных член (константа)	1
Модель (после константы)	r–1
Остаток	N–r			—

F(R) проверяет гипотезу . Если полученное значение достоверно, можно заключить, что данные согласуются с выбранной моделью.

F(М) проверяет гипотезу . Эта гипотеза определяет приемлемость модели для значимой величины вариации у-переменной.

F(R_m) проверяет гипотезу о влиянии модели на вариацию в у-переменной после проверки F(М). В однопутевой классификационной модели F(R_m) проверяет гипотезу равенства всех i-градаций независимого параметра «b» между собой.

Пример.

В результате бонитировки семи коров различной кровности получили следующий набор данных (по 100-балльной шкале):

Чистопородные	Полукровки	Трехчетвертные
73	78	84
67	82	90
76
216	160	174

Требуется определить племенную ценность групп животных различной кровности (по итогам проведенной бонитировки) и ответить на вопросы:

1. Имеют ли чистопородные животные одинаковую племенную ценность с помесями?

2. Различаются ли полукровные и трехчетвертные животные по племенной ценности?

Для ответа на поставленные вопросы можно использовать модель однопутевой классификации:

,

15. с₁ – чистопородные;

с₂ – полукровные;

с₃ – трёхчетвертные;

е – остаточный эффект ~ .

Согласно общей формуле , имеем:

.

Определяем суммы квадратов:

;

;

;

;

.

Оценки для животных каждой кровности имеет вид:

– для чистопородных;

– для полукровных;

– для трёхчетвертных.

Вариансы оценок описываются из диагоналей :

.

Таблицу анализа вариансы можно представить в следующем виде:

Источник	df	Суммы квадратов	Средний квадрат	F-соотношение
Константа	1	43558	43558	2562,23**
Кровность	2	276	138	8,11*
Остаток	4	68	17	—

Следовательно, нами отвергается гипотеза с₁=с₂=с₃ и делается заключение, что племенная ценность животных разной кровности различна. Для ответа на вопрос, имеют ли чистопородные животные такую же племенную ценность, что и поместные, необходимо проверить гипотезу:

.

;

;

;

;

;

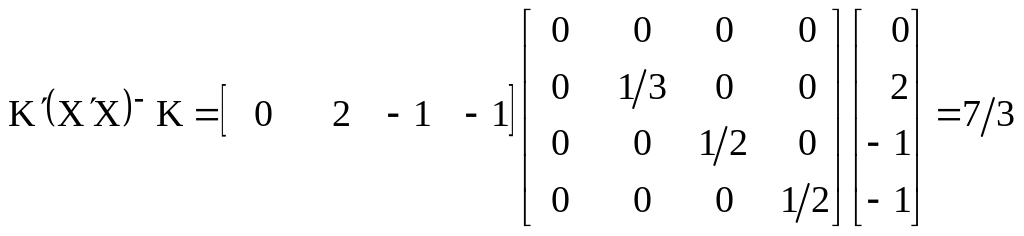для составляет 7,71.

Следовательно, нулевая гипотеза отвергается и нами делается заключение, что помеси по своим племенным качествам лучше, чем чистопородные животные.

Для проверки второй гипотезы – о различии в племенной ценности между полукровными и трёхчетвертными животными определяем .

;

;

;

;

для составляет 7,71.

Следовательно, нулевая гипотеза не может быть отвергнута и нет оснований утверждать, что с повышением кровности увеличивается и племенная ценность помесей.