2. Множественная линейная регрессия

В практике зачастую встречаются ситуации, когда на результирующий параметр влияет ряд факторов. В таком случае модель линейной регрессии можно представить в виде:

,

6. у – результирующий параметр;

а – свободный член регрессии;

b₁ … b_k – искомые коэффициенты множественной регрессии;

х₁ … х_k – независимые аргументы (факторы).

Уравнение для i-ого наблюдения:

.

Представим а=b_ix_i0 со всеми x_i0=1. Тогда модель i-ой записи перепишется как:

.

Определив наборы переменных и факторов как матрицы (вектора):

; ; ; ,

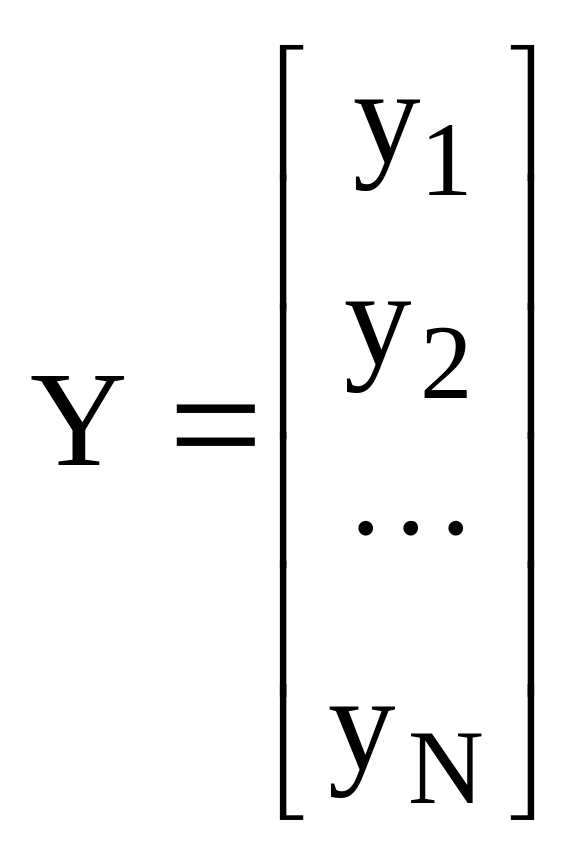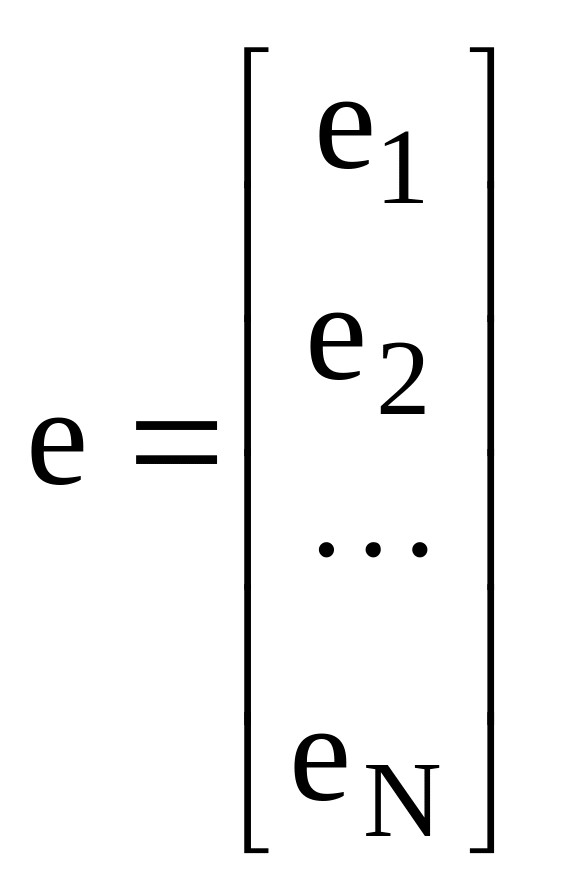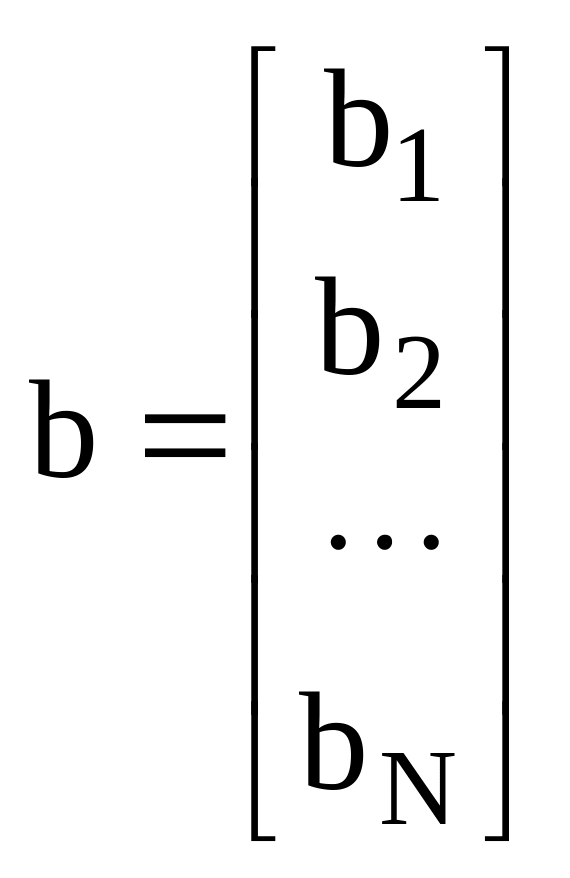представим модель в матричной форме:

.

Для получения наилучшей оценки на модель накладываются следующие ограничения:

,

,

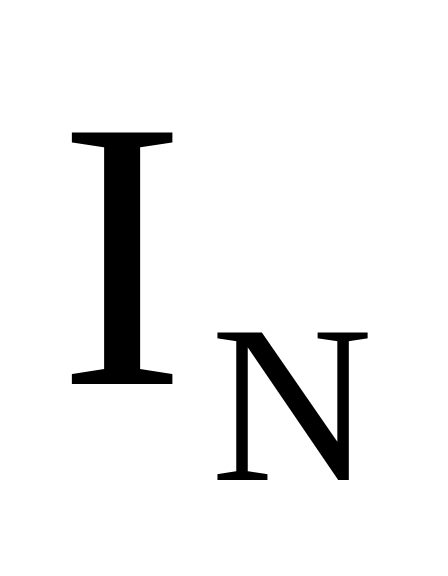7. – единичная матрица ранга N.

Методика определения искомых коэффициентов «b»:

1. Определить вариансу ошибки:

.

2. Получить частные дифференциалы по «b»:

.

3. Приравнять частный дифференциал к 0:

.

4. Решить уравнение относительно «b»:

,

.

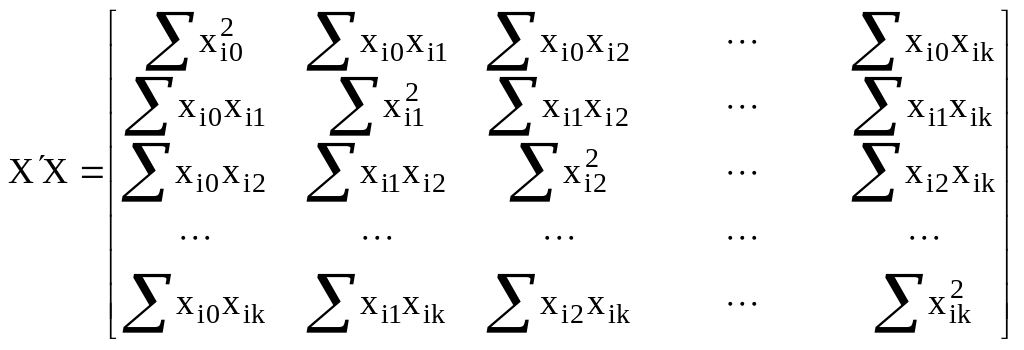Поскольку по определению х_i0=1, то

.

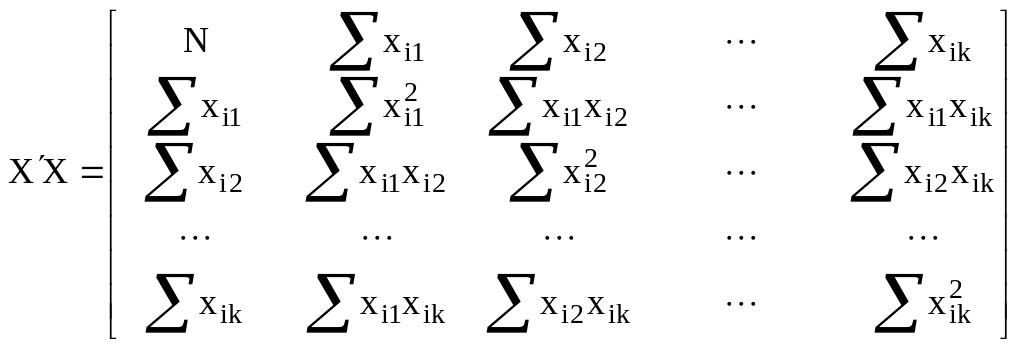Соответственно:

.

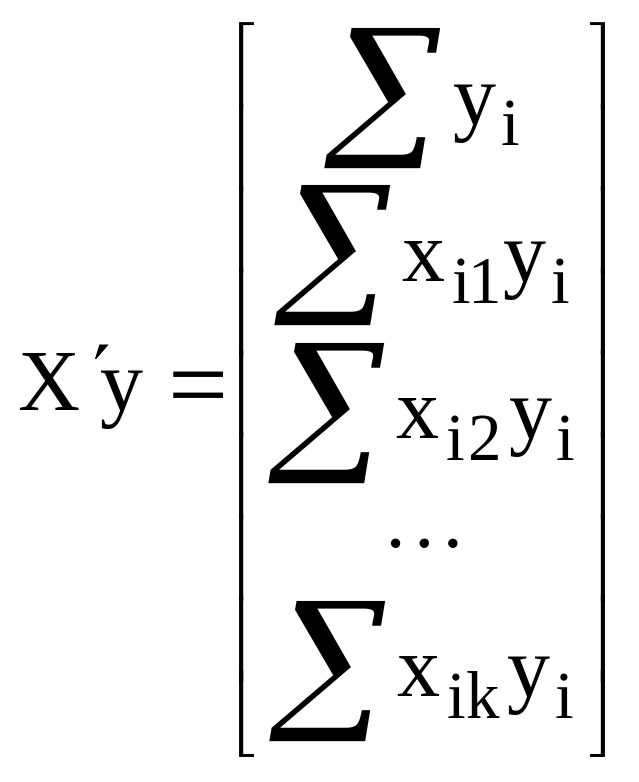Анализ вариансы:

1. Варианса ошибки оценивается как:

,

8. ;

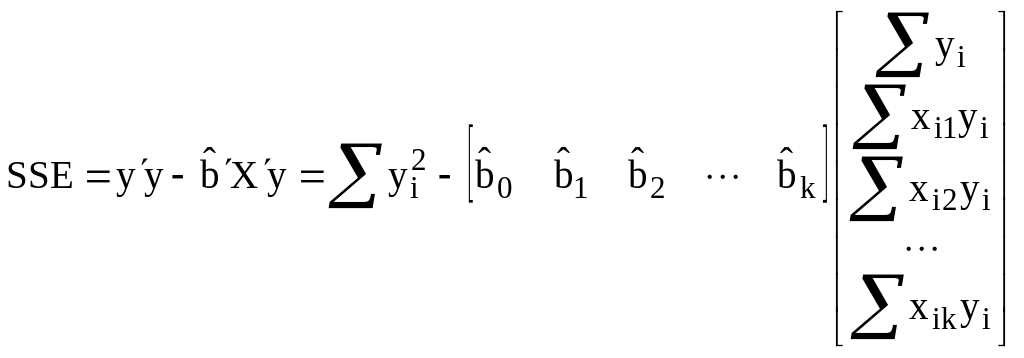r – число независимых параметров в уравнении множественной регрессии, включая свободный член.

1. Варианс-ковариансная матрица оценки « »:

.

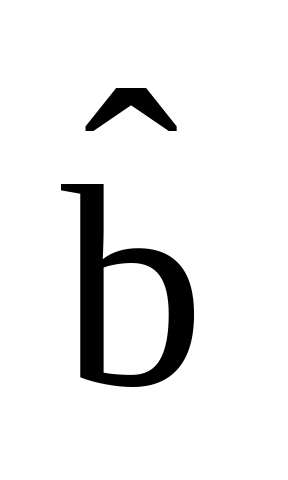В итоге получается матрица размером rхr. Диагональные элементы матрицы представляют собой вариансы, а внедиагональные – ковариансы; матрица – симметричная. Стандартные ошибки оценок определяются как корни квадратные из соответствующих значений варианс.

2. Вычисление сумм квадратов.

   1. Общая сумма квадратов:

.

2. Регрессионные (редуцированные) суммы квадратов:

.

3. Значимые (факториальные) суммы квадратов:

.

4. Регрессионные суммы квадратов, скорректированные на значимые:

.

5. Общие суммы квадратов, скорректированные на значимые:

.

6. Остаточные (ошибочные) суммы квадратов:

, или .

4. Точность построенного уравнения определяется коэффициентом множественной корреляции (детерминации):

(обычно умножается на 100%).

4. Проверка свойств распределения:

~ ;

~ ;

~ ;

F(R) проверяет гипотезу Н₀: b=0 против гипотезы Н_a: b≠0

F(М) проверяет гипотезу Н₀: Е( )=0 против гипотезы Н_a: Е( )≠0

F(R) проверяет гипотезу

против .

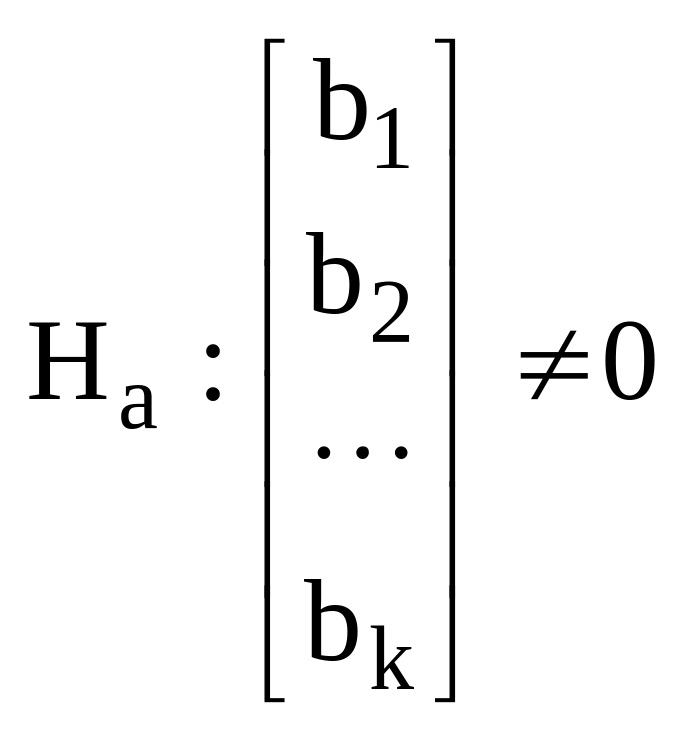4. Редуцированные модели.

Значимость включения отдельных конкретных значений « » определяется посредством применения уменьшенных моделей.

F-соотношение имеет вид:

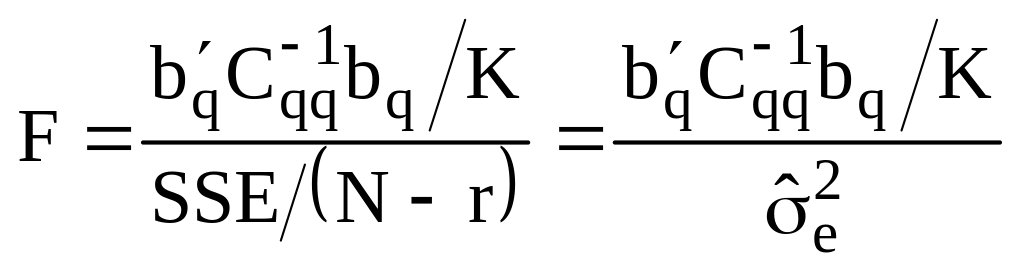
9. q – поднабор из общего набора векторов «b»;

К – число проверяемых векторов;

С_qq – инверсия частной матрицы (размер и структура матрицы определяется набором «b» – параметров из общей модели).

Полученное значение сравнивается с табличным значением Fisher-criteria для (К, N-r) степеней свободы.

Пример.

В процессе эксперимента получили следующий набор данных:

Свиноматка	Число поросят в опоросе, гол.	Возраст опороса, мес.	Порядковый номер опороса
1	6	11	1
2	9	17	2
3	8	13	1
4	12	23	3
5	11	25	3
6	7	12	1
7	10	18	2

Предполагается использовать следующую модель множественной регрессии:

,

10. у_i – размер помета i-ой свиноматки;

а – свободный член уравнения;

b₁ – коэффициент регрессии размера помета на возраст опороса свиноматки;

b₂ – регрессионный коэффициент размера опороса на порядковый номер опороса;

e_i – случайная ошибка с нулевой средней и вариансой .

Система нормальных уравнений:

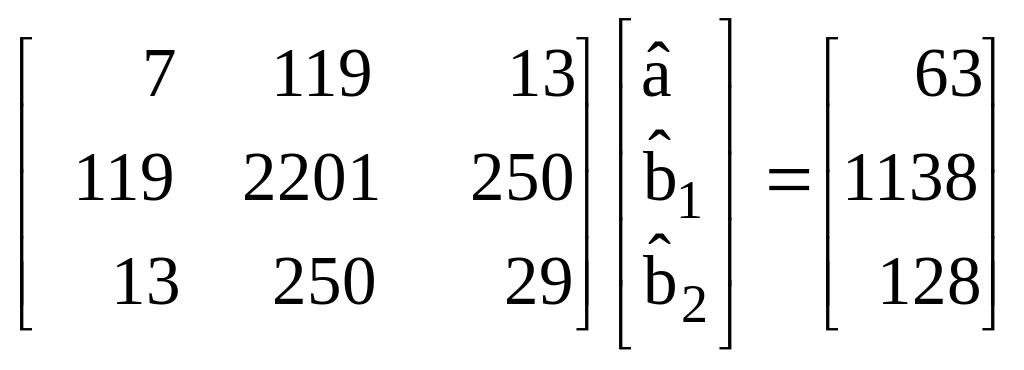
приводит к следующим решениям:

.

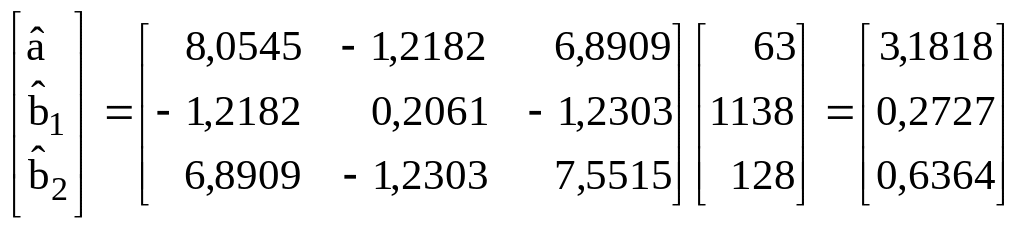На основе сумм квадратов, вычисленных по общепринятым методикам, таблица анализа вариансы выглядит следующим образом:

Источник	Число степеней свобода	Сумма квадратов	Средний квадрат	F-критерий	Р>F
Регрессия	2	25,2727	12,6364	18,53**	0,0095
Возраст опороса	1	0,3610	0,3610	0,53	0,5072
Порядковый номер опороса	1	0,0536	0,0536	0,08	0,7930
Ошибка	4	2,7273	0,6818

Квадрат регрессионного значения проверяет гипотезу против альтернативной гипотезы и, основываясь на значимом значении F-критерия (Р<0,01), Н_a гипотеза принимается. Вместе с тем ни один из показателей, включенных в модель и анализируемых раздельно, не дает значимого критерия (Р₁=0,51 и Р₂=0,79). Это на первый взгляд выглядит парадоксом, и нами должна приниматься нулевая гипотеза в обоих случаях.

В этой ситуации часто делается ошибочный вывод о том, что ни номер опороса, ни возраст матки не оказывают значимого влияния на число поросят в опоросе. Однако единичное число степеней свободы при анализе вариансы в данном случае показывает, что влияние возраста опороса определялось после принятия значимости порядкового номера опороса и наоборот. Если нами будет устанавливаться влияние указанных аргументов на размер помета раздельно, т.е. используя субмодели

и ,

то каждый из них окажется значимым (b₁=0.376±0,056 и F(H)=45,34**; b₂=2,26±0,36 и F(Н)=40,33*). Следовательно, можно сделать вывод, что включать в модель показатели возраста свиноматки и порядкового номера опороса одновременно нет необходимости, но один из них должен быть включен обязательно.