4. Решение, основанное на определении истинного коэффициента γ в процессе вычислений

Необходимо на этапе ввода информации определить начальное значение , которое имеет связь с коэффициентом наследуемости (повторяемости) согласно:

1. в случае, если требуется определять передающую способность животного (племенная ценность животного по фактической продуктивности его потомков).

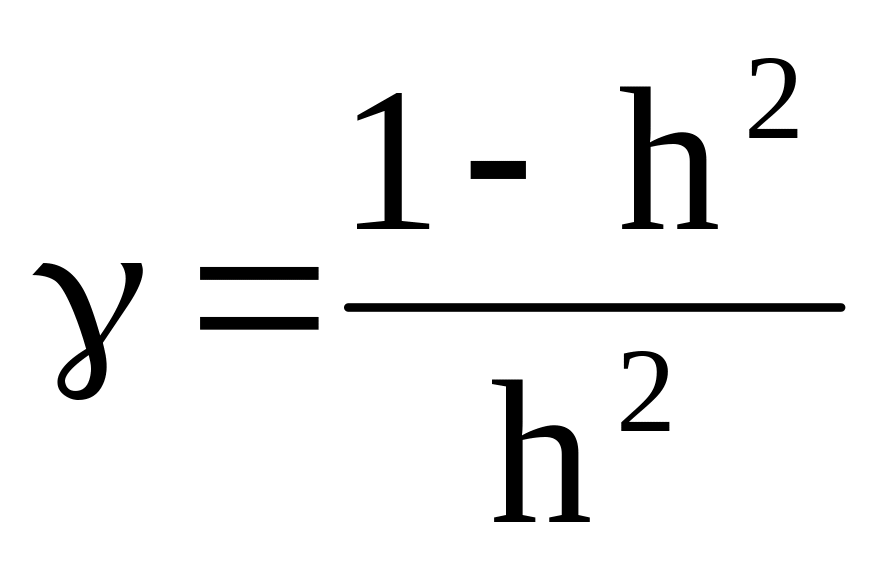2. , когда наблюдаемая переменная представляет собственный показатель продуктивности оцениваемого животного.

Для первого цикла итерационного процесса принимаем .

Решения в этом случае будут представлены в виде:

.

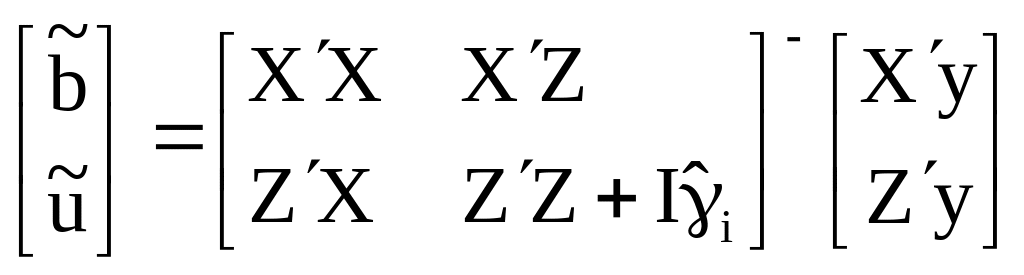В скалярной форме вектор решений описывается как:

.

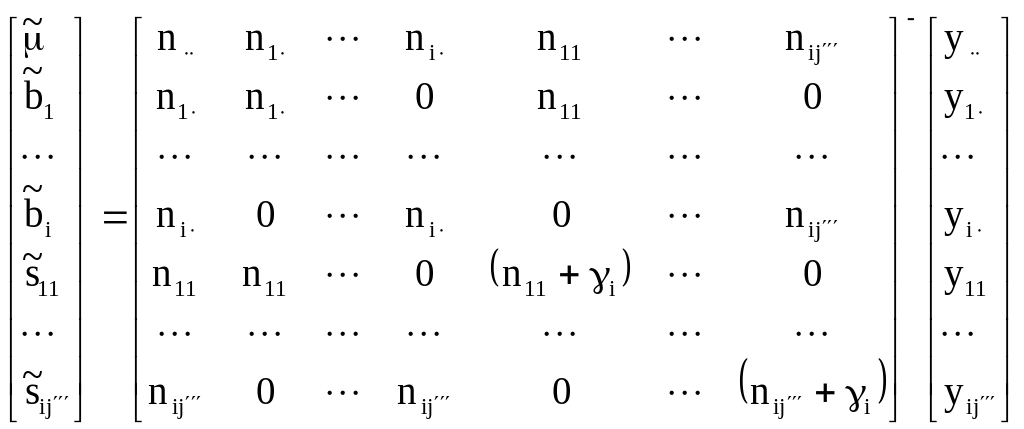Ранг инверсии складывается из:

.

Положив и приведя матрицу к полному рангу, получаем решение для и .

Для оценки разности , как обычно, используется оценочная функция . Эта оценка несмещенная, однако минимальная варианса разности будет получена лишь при (истинное значение).

Оценка вариансы ошибки проводится традиционно:

.

Отметим вновь, что если то не будет несмещенной.

В арианса разницы оценивается как , и корень квадратный из вариансы дает стандартную ошибку (отклонение) разницы.

При проверке гипотезы для всех (или выборочных) значений i необходимо вычислить:

и сравнить

,

2. f – число строк в матрице K′.

Эти результаты могут быть представлены в традиционной табличной форме.

Таблица 2.31.

ANOVA

Источник	df	Суммы квадратов	Средний квадрат	F-тест
b-параметр	i-1
Остаточный эффект	N-i			—

Совместные решения для , , и могут быть описаны с использованием метода ограниченного максимального правдоподобия. Для первого цикла итерации вычисляем:

,

3. q – число S_ij-градаций по всей анализируемой совокупности.

Имея оценки и , можно вновь переоценить коэффициент γ и повторять итерационный процесс до тех пор, пока не будет равной с заданной степенью точности. В этом случае можно считать, что (правдивое значение), и результаты решения системы уравнений будут представлять BLUE для фиксированных параметров и BLUP для рэндомизированных эффектов.

Пример.

Предположим, что на племпредприятии имеются быки двух пород. Исходные данные о количестве и объеме эякулятов, полученных от быков за определенный период, сведены в следующую таблицу:

Порода	Бык	Объём эякулята, мл
1	1	4,6;	5,1;	4,4;	5,9;	5,5;	6,0;	4,5;	5,0	(n=8)
1	2	5,3;	5,2;	6,1;	4,9;	5,8;	5,7;	(n=6)
2	1	5,8;	5,9;	6,4;	6,7;	6,4;	6,0;	6,9	(n=7)
2	2	5,3;	5,3;	6,2;	7,0;	5,8;	(n=5)
2	3	4,9;	6,2;	6,5;	5,7;	4,9;	6,5;	6,4;	6,9;	6,1;	(n=9)

Требуется спрогнозировать ценность быков по показателю «объем эякулята», определить межпородные различия, проверить гипотезу об эквивалентности влияния пород на объем эякулята.

Наиболее приемлемой для анализа выглядит модель:

,

4. y_ijk – объем эякулята;

µ – популяционная константа;

b_i – фиксированный эффект «порода»;

s_ij – рэндомизированный эффект быка;

e_ijk – остаточный эффект ~ .

В матричном виде:

.

Допустим, что начальное значение коэффициента γ равно 4, что соответствует коэффициенту повторяемости r=0,20.

Тогда решения системы линейных уравнений можно представить в виде:

.

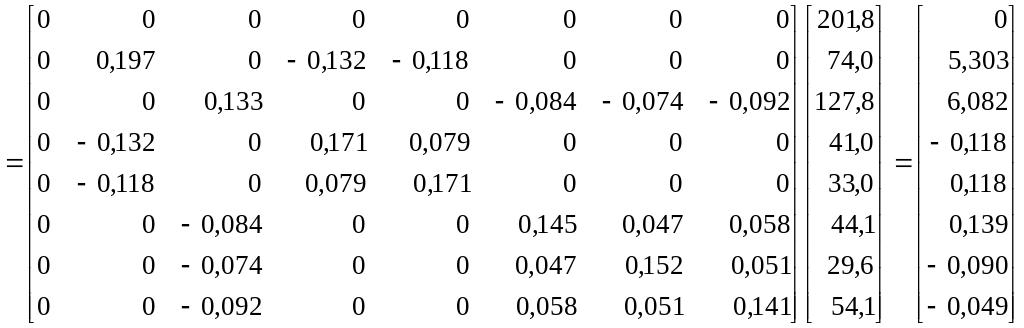Следующий этап оценки – определение остаточной вариансы:

.

В двухпутевой гнездовой классификации разница между породами может быть описана оценочной функцией:

.

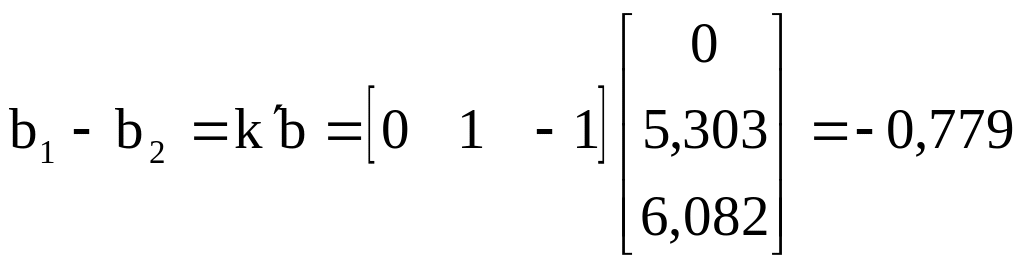Варианса различий в породных эффектах выражается как:

.

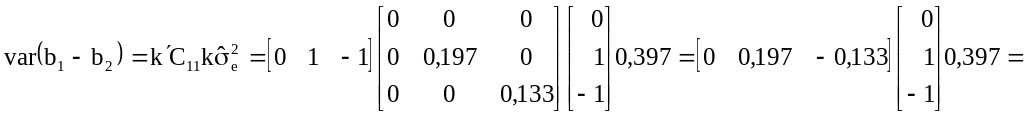
Т огда .

Предсказанная ценность быков по объему эякулята будет определяться как :

.

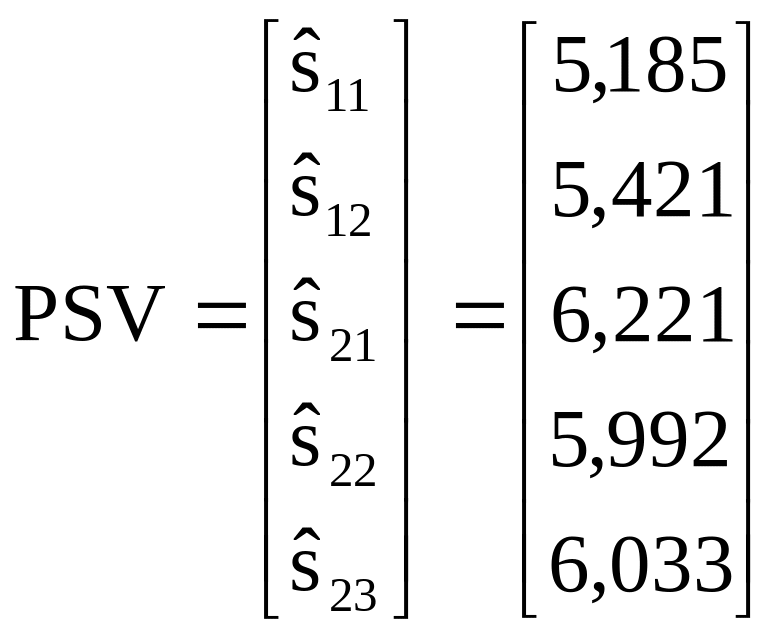Определение различий между быками-производителями выполняется следующим образом:

;

.

Т огда .

При принадлежности быков к разным породам функция разности имеет вид:

и варианса оценки:

,

,

что является достоверным.

Следовательно, быки двух исследуемых пород достоверно различаются по показателю «объем эякулята», и эффект «порода» обязательно должен присутствовать в модели.

Полученные результаты, как и в двухпутевой кроссклассификации, не будут являться BLUE и BLUP до тех пор, пока выбранный коэффициент отношении не станет равен истинному. Используя методику ограниченного максимального правдоподобия, вычисляем очередное значение :

.

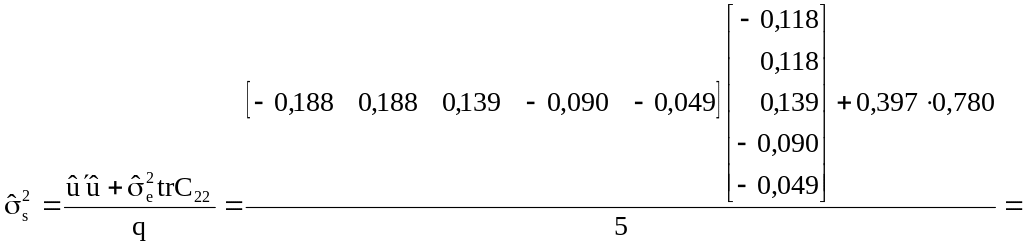
Затем, вычисляя новое текущее значение γ, необходимо повторять всю последовательность операций, пока γ_i-1, "в станет равной γ_i. Только в этом случае оценки для b-будут представлять BLUE, а решения для s-эффектов – BLUP.

1Выбор значения для первого шага итерации влияет только на временные затраты вычислительного процесса, но абсолютно не влияет на конечный результат прогноза.

17