2. Решение с заменой случайных эффектов на фиксированные

Решения для фиксированных эффектов (когда соотношение заранее неизвестно) представляются в виде:

.

Формализуя каждый элемент матрицы, получаем:

.

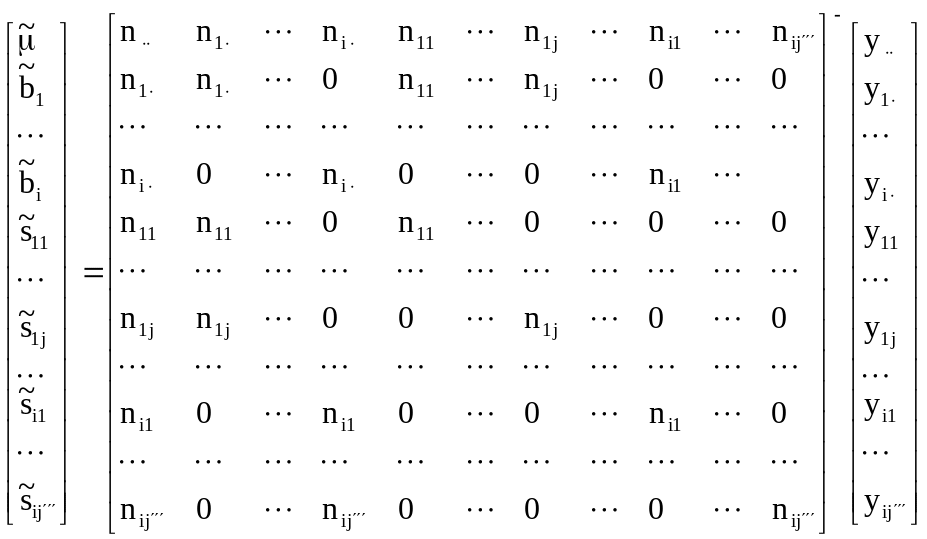Ранг [ХZ] матрицы равен количеству градаций в s-параметре за минусом единицы, т.е. , поэтому для получения инверсии обычно представляют . Очевидно, что при решении системы корни уравнений не являются уникальными и зависят от вида полученной инверсии. Различия же между s-параметрами не зависят от принятой структуры инверсии и могут быть описаны при помощи оценочной функции с прогнозом вариансы ошибки:

Прямое сравнение двух уровней параметра «b» под фиксированную модель не может быть выполнено, т.е. не является оценочной функцией. Вместе с тем оценочная функция представляется как и, очевидно, зависит от выбора М′. Наиболее часто для оценки различий между уровнями «b» применяется матрица М′ следующего представления:

.

.

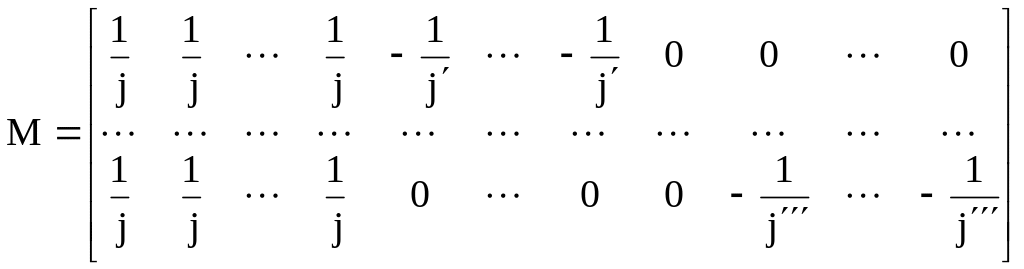Общая формула для оценки вариансы выглядит как:

,

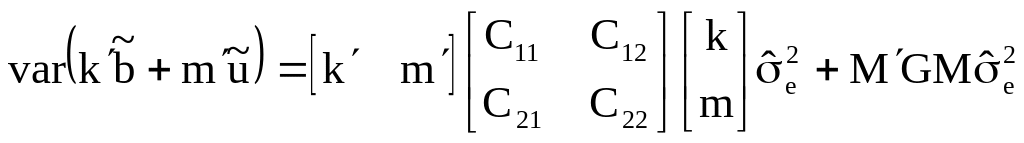где .

Тогда:

.

Оценка факториальной и ошибочной варианс проводится согласно:

;

.

Методика определения предполагает:

1. Вычисление 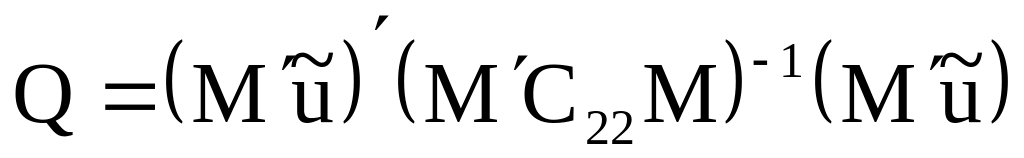, где М′ предусматривает попарное сравнение всех s-параметров внутри каждого уровня i.

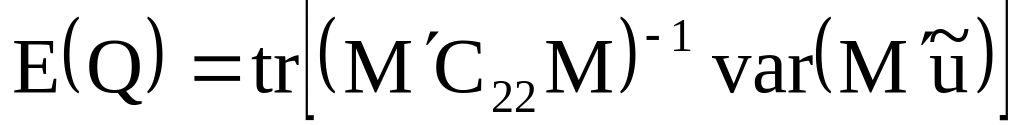2. Вычисление с .

Тогда: – промежуточная форма представления.

3. Приравняв , получаем:

.

4. Математическое ожидание от МS для (S|b) определяется как 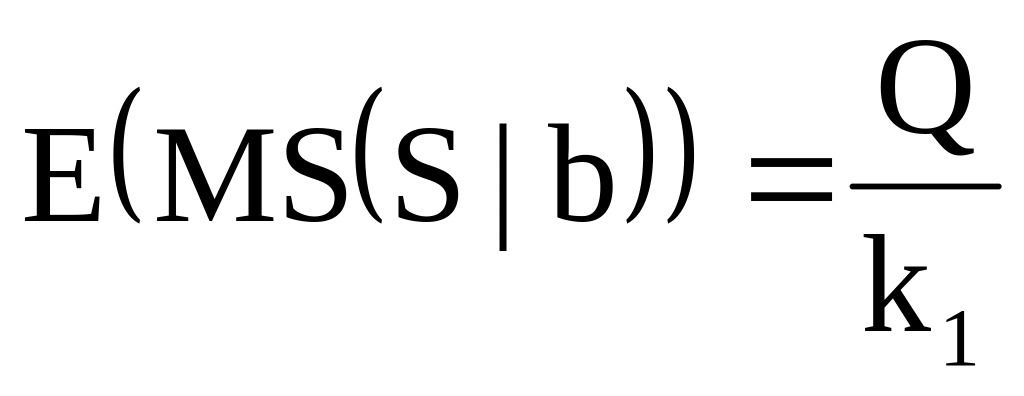, где k₁ – число степеней свободы, равное коэффициенту при .

Следовательно, .

5. Решение для факториальной вариансы:

.

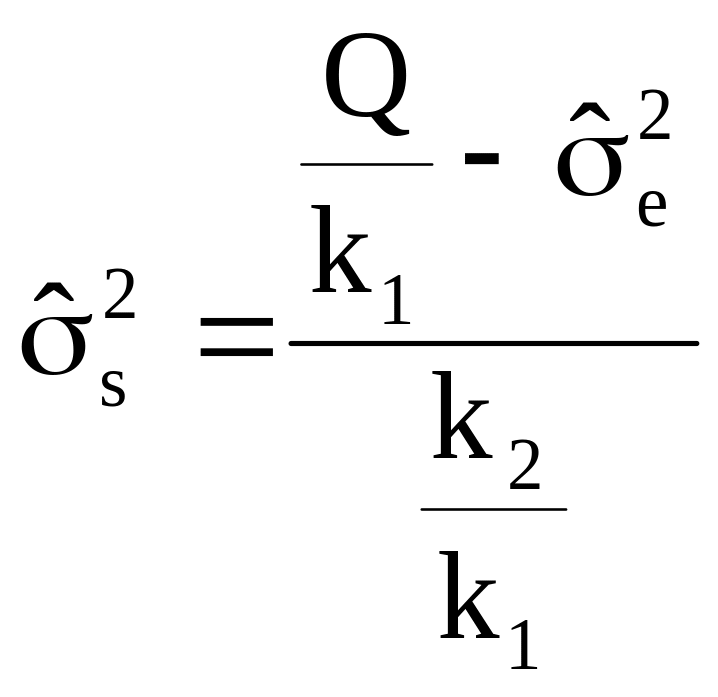Подставляя полученные численные значения и , получаем оценку .

3. Решение, основанное на игнорировании случайных эффектов

Фиксированные эффекты могут быть оценены с помощью операционной модели:

,

где рэндомизированные эффекты игнорируются.

В матричной форме решение представляется в виде:

.

Переходя к скалярным значениям, имеем:

.

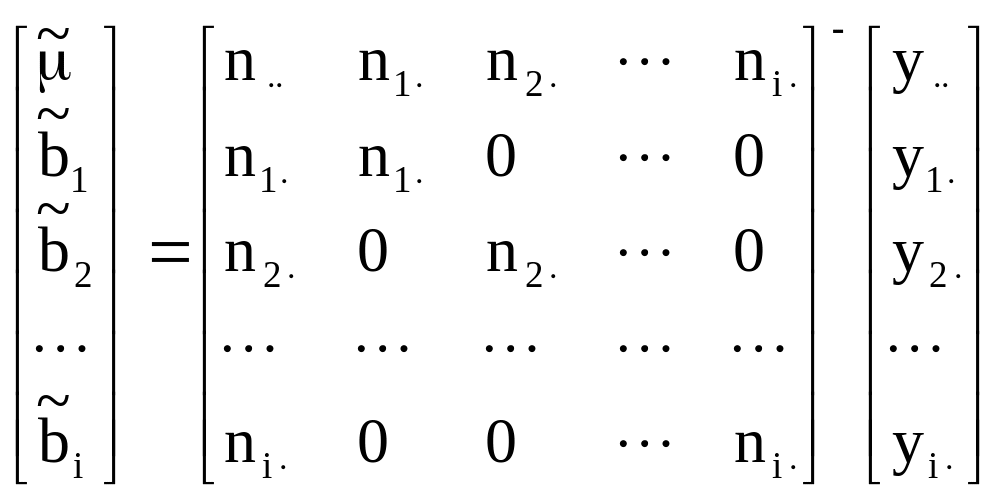Рант инверсии равен (i-1) и, положив , получаем решение для каждого . Оценить разницу между любыми можно при помощи оценочной функции . Варианса разности определяется:

,

где .

В окончательном виде , где K₁ и K₂ – числовые коэффициенты.

В данном случае величины и неизвестны, однако оценить их можно согласно следующей методики:

1. Определить 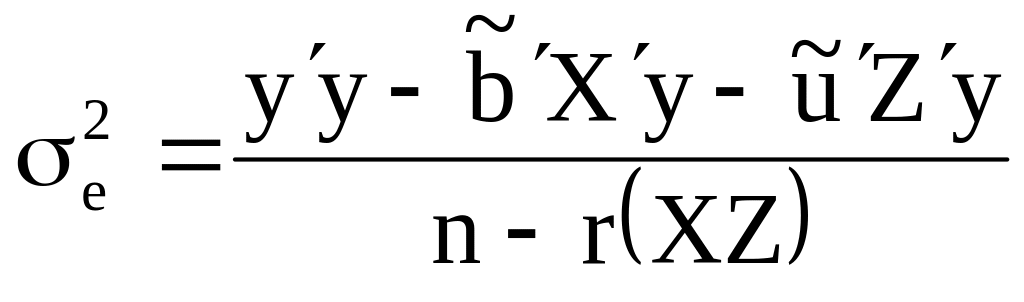, где 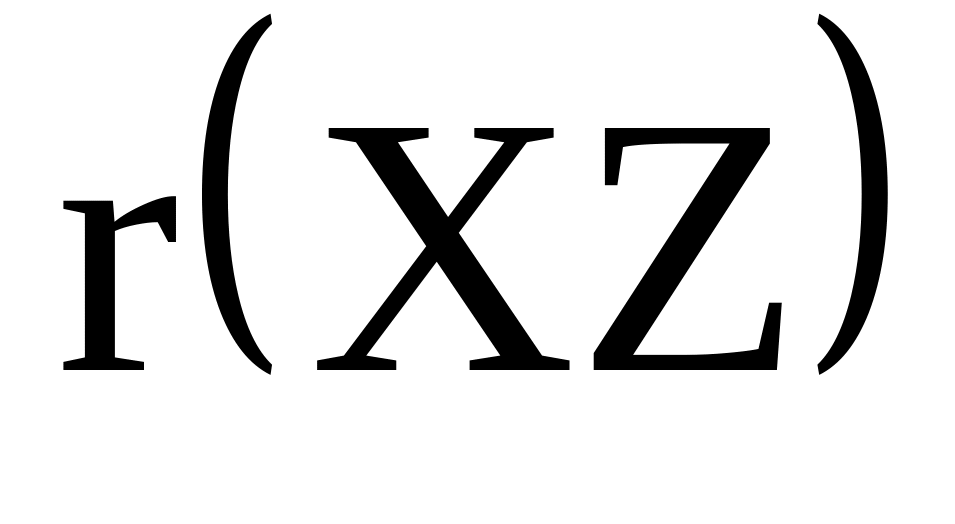– ранг инверсии для модели с фиксированными эффектами.

2. Используя модель с представлением случайных эффектов как фиксированных и наложив методику расчета, описанную в п. 2.7.2.2, получаем:

,

1. t₁ и t₂ – определенные коэффициенты.

В результате, такой способ представления эффектов дает очень приближенное значение прогноза отдельных параметров и их влияния на результирующую наблюдаемую переменную. Поэтому его применение в практике очень ограничено.