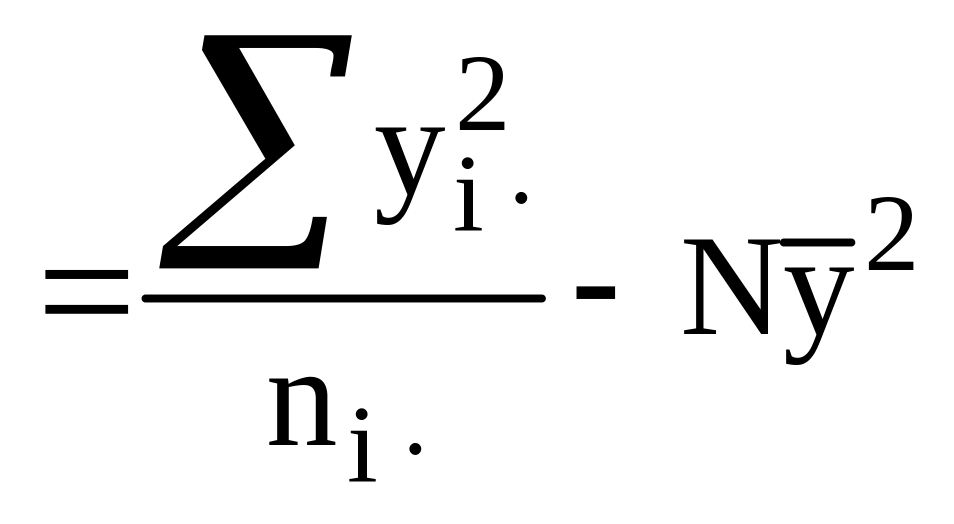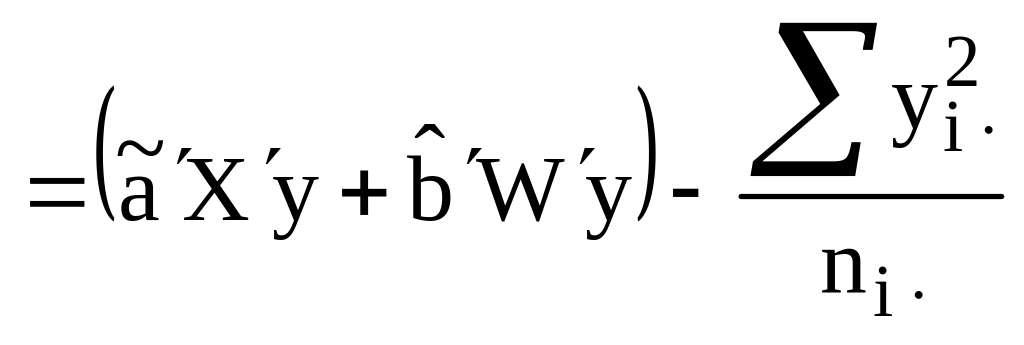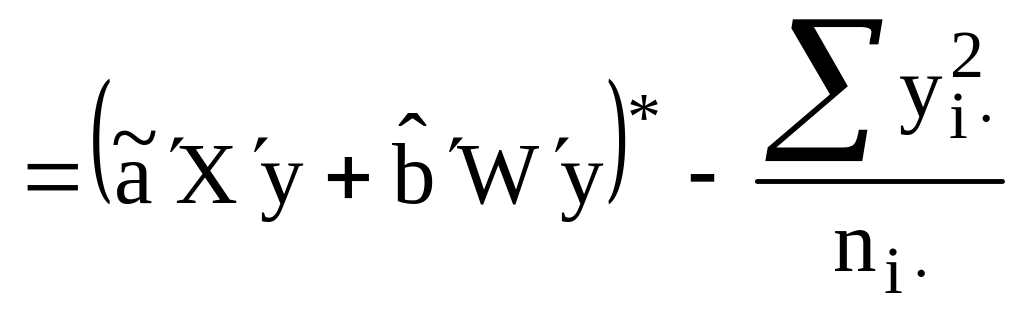2. Внутриклассовая регрессия

Внутриклассовая регрессия ковариантного анализа предусматривает, что наклон ковариантной линии в различных дискретных уровнях h_i неодинаков. Другими словами, для всех случаев существует не единственная оценка « » (как в предыдущей однопутевой классификации), а оригинальный для каждого уровня h_i коэффициент частной регрессии параметра «w» на результирующий вектор «y».

Уравнение модели внутриклассовой регрессии анализа ковариант практически не отличается от предыдущего:

.

Разница лишь в том, что коэффициент «b_i» является уникальным для каждого i-уровня.

В матричной форме:

.

При переходе к скалярным значениям элементов матрицы получаем:

.

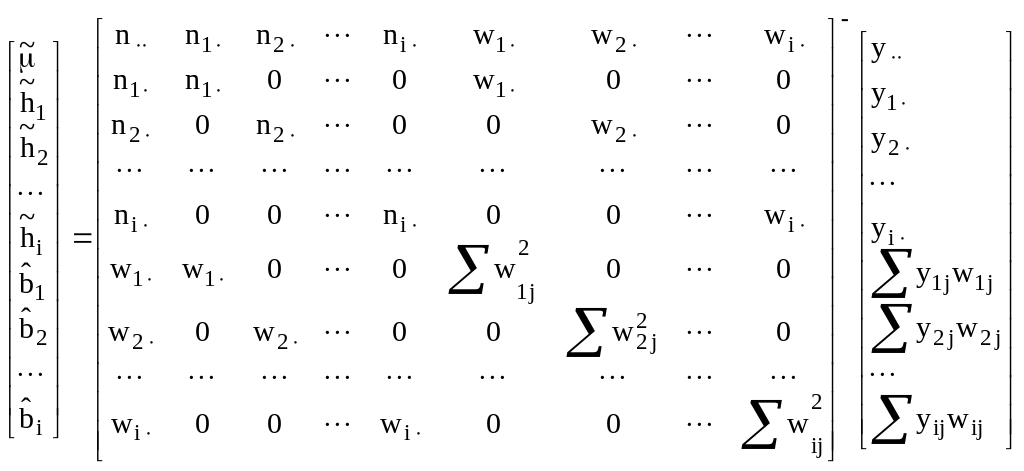Рант матрицы [ХW] рассчитывается из рангов матриц - составных частей:

.

Как правило, наименее значимый параметр для исследователя – оценка , поэтому для получения обобщенной инверсии чаще всего значения первой строки и первой колонки матрицы ХW игнорируются (т.е. принимается ).

Строго говоря, различия между h_i-параметрами оценимы в данной модели, однако они представляют малый интерес, так как должны быть произведены при w_ij = 0 для каждого «i». Более значима оценка типа для данного w_ij. Поскольку , то оценки, такого типа могут быть произведены. Варианса оценки определяется как:

,

2. K – оценочная функция для h-параметра;

m – оценочная функция для w-коварианта.

Оценка ошибочной вариансы описывается из формулы:

.

Анализ вариансы для моделей внутриклассовой регрессии можно представить в виде следующей таблицы:

Таблица 2.24.

ANOVA

Источник	df	Суммы квадратов	Средний квадрат	F-тест
Общепопуляционное значение	1
h-эффект (после µ)	i-1
Ковариата (после µ, h)	i
Совокупная (после µ, h)	1
Разница	i-1
Остаточное значение	N-2i			—

*3начение при вычислении сумм квадратов для совокупной коварианты определяется из модели, когда коэффициент «b» одинаков для всех уровней «i» (аналогично однопутевой классификации).

В табл. 2.24 представляет собой числитель сумм квадратов для проверки эквивалентно для всех уровней i.

Разница сумм квадратов есть числитель для проверки Н:b_i эквивалентны для всех i. Если гипотеза относительной эквивалентности «b_i» принимается, то необходимо переписать модель с идентичным коэффициентом «b» всех уровней i.

Пример.

Набор данных для анализа идентичен входной информации, приведенной в предыдущем разделе:

Чистопородные		Полукровные		Трёхчетвертные
Число баллов	Возраст	Число баллов	Возраст	Число баллов	Возраст
74	3	76	2	85	4
68	4	80	4	93	6
77	2
219	9	156	6	178	10

Требуется определить, существует ли разница в коэффициентах регрессии племенной ценности на возраст животных между группами генотипов.

Модель анализа выглядит следующим образом:

.

Применительно к входным данным вектор решений имеет вид:

.

В этом примере наибольший интерес представляет оценка племенной ценности животных различных возрастов в пределах их генотипа. Например, оценка племенных качеств 2-летней чистопородной коровы производится как:

(баллов).

Варианса оценки описывается следующим образом:

,

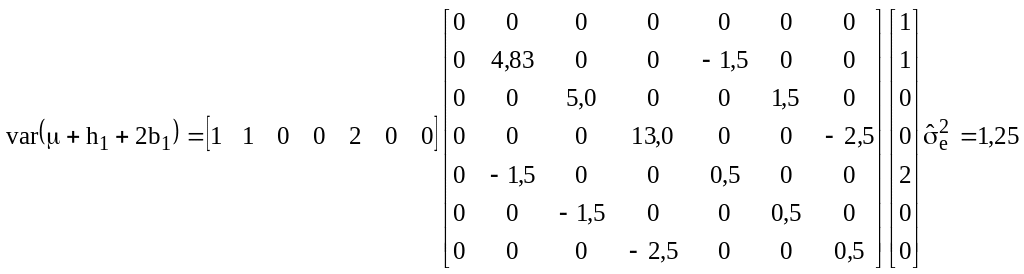
где оценка варианс вычисляется из:

,

а в окончательном виде:

.

Таблица анализа вариансы в случае внутриклассовой регрессии может быть представлена следующим образом:

Таблица 2.24.

ANOVA

Источник	df	Суммы квадратов	Средний квадрат	F-тест
Константа	1		43687	1628,29***
h|µ	2		155	5,88
Ковариата	3		26,83	1,00
	1		1,5	0,06
Разница	2	79	39,5	1,47
Остаток	3		26,83	—

В результате можно заключить, что не существует значимых различий в коэффициентах регрессии племенной ценности животных различных генотипов на возраст.