2. Модели с «потерянными» данными

При анализе массовых данных, как правило, возникают ситуации, когда ряд значений взаимодействий отсутствуют. Например, при оценке быков на разных уровнях продуктивности стад отсутствуют дочери отдельных быков в каких-либо градациях хозяйств по удою. Такого рода ситуации могут быть проанализированы при помощи моделей с «потерянными» данными.

В общем виде входная модель для анализа не отличается от предыдущей:

,

4. y_ijk – наблюдаемая переменная;

µ – общепопуляционная константа;

r_i – первый фиксированный эффект (i=1, 2, …, p);

s_j – второй фиксированный эффект (j=1, 2, …, q);

rs_ij – эффект взаимодействия между i-ым уровнем r-параметра и j-ой градацией s-параметра;

e_ijk – случайный остаточный эффект ~ .

Нормальное уравнение в этом случае:

,

откуда

.

Ранг матрицы (Х′Х) в моделях с «потерянными» данными всегда равен числу известных (присутствующих) интеракционных субклассов, и уравнение решений упрощается до:

,

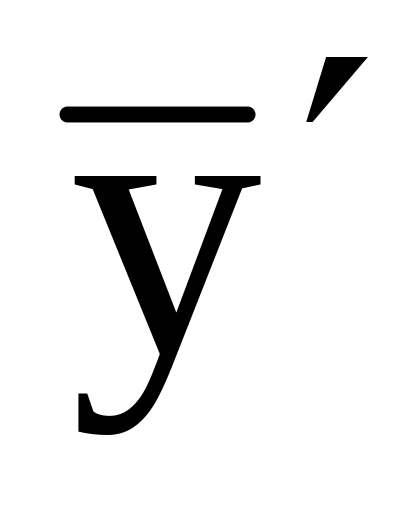5. – вектор наблюдаемых взаимодействий.

Тогда:

;

;

;

;

6. r(x) – ранг матрицы (Х′Х).

Как и в предыдущих случаях, уравнение оцениваемо для любого наблюдаемого y_ijk и оценивается при помощи с вариансой .

Необходимо заметить, что не может быть оценено для любого «потерянного» интеракционного эффекта, т.к. не существует наблюдения на такой субкласс взаимодействия. Вместе с тем оценочную функцию часто можно описать путем определения двух разниц θ, каждая из которых содержит потерянное значение µ_ij.

Таблицы анализа варианс в зависимости от решаемых задач имеют следующие структуры:

Таблица 2.14.

ANOVA

Источник	df	Суммы квадратов	Средний квадрат	F-тест
Популяционная константа	1
	t-1
Остаточный эффект	N-t			—

Таблица 2.16.

ANOVA

Источник	df	Суммы квадратов	Средний квадрат	F-тест
Популяционная константа	1
r|µ	p-1
s|µ,r	q-1
rs|µ,r,s	t-p-q+1
Остаточный эффект	N-t			—

^* для модели .

Таблица 2.17.

ANOVA

Источник	df	Суммы квадратов	Средний квадрат	F-тест
Популяционная константа	1
r|µ	p-1
s|µ,r	q-1
rs|µ,r,s	t-p-q+1
Остаточный эффект	N-t			—

^* для модели ;

t – число наблюдаемых интеракционных значений.

Проверки гипотез, ассоциированных с , , , выполняются аналогично приведённым в разделе 2.5.1.

Пример.

Вернемся к набору данных, приведенных в разделе «Двухпутевая перекрестная классификация».