1. Базисные определения матричной алгебры

Матрица представляет собой упорядоченный набор чисел, записанный в виде прямоугольника. Все числа матрицы носят название элементов.

Порядок матрицы – число строк и колонок, составляющих исходную матрицу. Соответственно частными случаями матричных форм могут быть: квадратные матрицы – число строк равняется числу колонок; строчные вектора – матрицы, содержащие только одну строку; колонковые вектора – матрицы, содержащие только одну колонку; скаляры - отдельные числа.

Матричные операции

Сложение

Если две или несколько матриц имеют один и тот же порядок, то они приспособлены для сложения. Сумма двух приспособленных для сложения матриц составляет новую матрицу, каждый элемент которой равняется сумме корреспондирующихся элементов исходных матриц. Например, суммой (S) двух исходных матриц:

и

будет являться матрица:

.

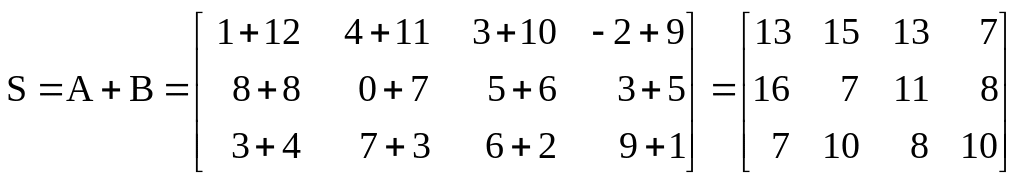Очевидно, что суммарная матрица имеет тот же порядок, что и исходные матрицы.

Вычитание

Матрицы приспособлены для вычитания, если все они имеют один и тот же порядок. Разностью двух матриц является новая матрица, каждый элемент которой представляет собой разность корреспондирующихся элементов исходных матриц. Например, разность вышеприведённых матриц А и В будет равна:

.

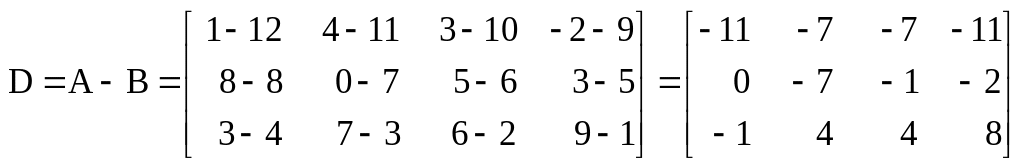Умножение

Операция матричного умножения может быть подразделена на три частных случая:

• умножение на скаляр;

• векторное умножение;

• умножение на матрицу.

Матрица, умноженная на скаляр, есть матрица, каждый элемент которой представляет собой произведение соответствующего элемента исходной матрицы на скаляр. Например, произведение 4А имеет вид:

.

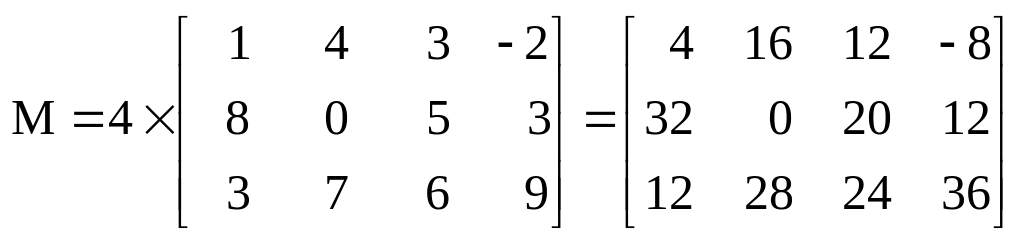Произведение строчного вектора на колонковый – это скаляр, представленный как сумма произведений корреспондирующихся элементов исходных векторов. Например, произведение двух векторов V' и у:

;

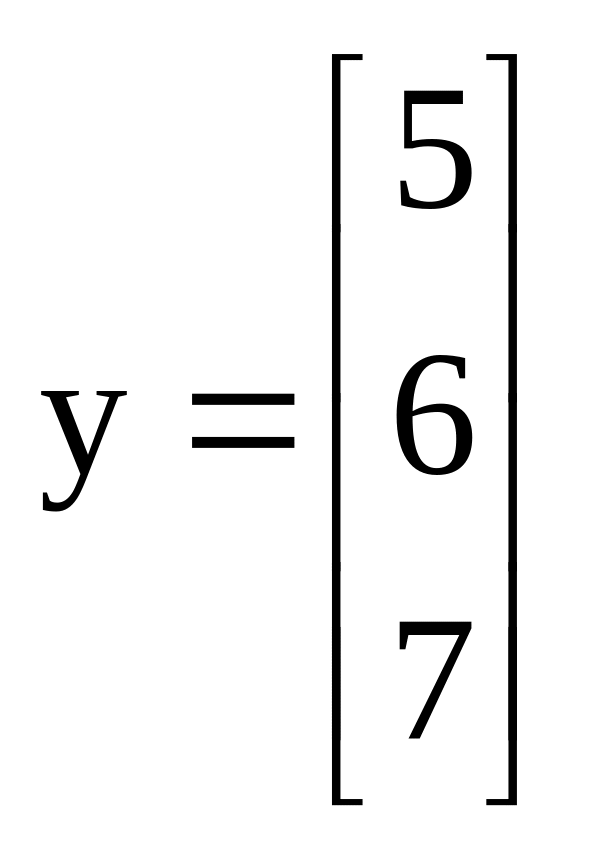
имеет вид:

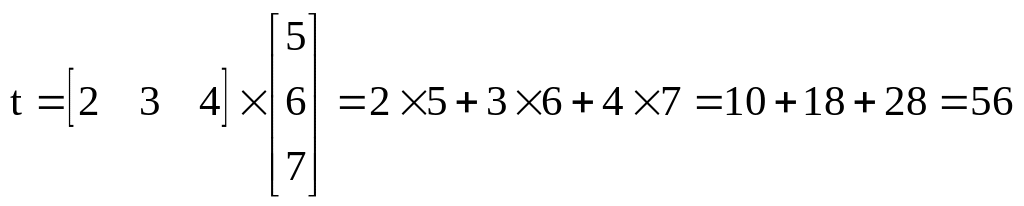
Принцип векторного умножения может быть распространен на умножение матриц, представленных как наборы векторов. Например, произведение АхВ двух матриц А и В:

и

имеет вид:

.

Очевидно, для возможности матричного умножения необходимо, чтобы число колонок матрицы-множимого было равно числу строк матрицы-множителя.

Транспонирование матриц

Транспонирование матриц – его операция замены строк исходной матрицы на корреспондирующиеся колонки и наоборот. Например:

.

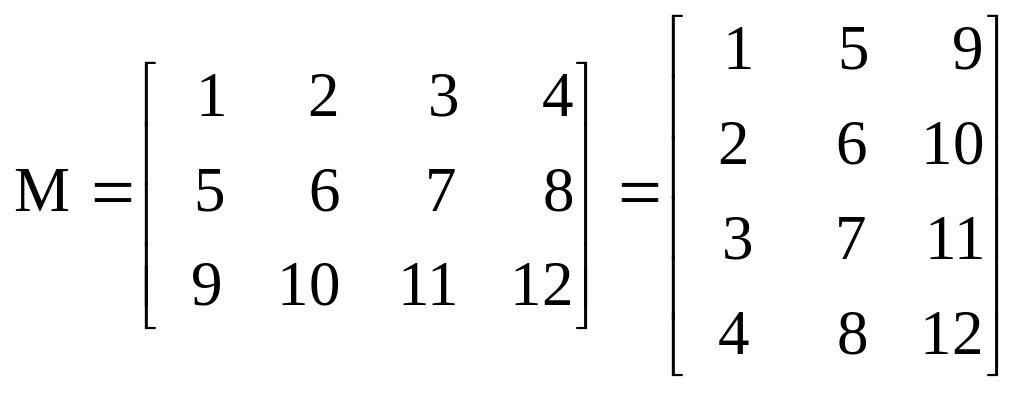Операция транспонирования произведения матриц может быть выполнена транспонированием каждой из исходных матриц, умноженных в обратном порядке, т.е. (АВ)′=В′А′.

Детерминант

Детерминант матрицы всегда выражается как число и существует только для квадратной матрицы. Знания о детерминанте необходимы для выполнения операции инверсии, которая является аналогом возведения выражения в минус первую степень в скалярной алгебре.

Детерминант скаляра (т.е. матрицы порядка 1х1) есть сам скаляр. Например, для А=[6] |А|=6. Детерминант матрицы второго порядка (2х2) – это разница между произведением диагональных и произведением вне диагональных элементов. Диагональными являются элементы, расположенные по диагонали от левого верхнего угла квадратной матрицы до нижнего правого. Например:

, то |А|=3х4-2х1=10.

Детерминант матрицы третьего порядка (3х3) может быть описан по правилу нахождения детерминанта матрицы 2х2, рассматривая исходную матрицу как набор трех матриц порядка 2х2. Причем каждое слагаемое детерминанта должно быть умножено на (-1)^i+j,

1. i – строка опорного элемента;

j – колонка опорного элемента.

Под опорным элементом понимается элемент матрицы, принадлежащий выбранным строке и столбцу, исключение которых приводит к матрице 2х2.

Например, если имеется матрица порядка 3х3:

,

то .

В данном примере опорными элементами выбраны элементы первой строки матрицы А: 5, 2, 4. В этом случае опорный элемент «5» имеет коэффициент «+1», поскольку он находится в первом ряду и первой колонке (i+j=1+1=2 и (-1)²=(+1)). Опорный элемент «2» имеет коэффициент (-1), поскольку для него i+j=3 и опорный элемент «4» имеет коэффициент (+1), так как i+j=4.

Детерминанты каждой из субматриц порядка 2х2 называются минорами. Например, минором второго элемента предыдущего примера является:

.

Произведение, полученное от умножения минора на корреспондирующийся элемент (-1)^i+j, называется кофактором.

При определении детерминанта очень важно то, что независимо от выбора опорной строки или опорного столбца, детерминант матрицы является величиной постоянной.

Например, для второй строки матрицы А:

.

Соответственно, для третьей строки матрицы А:

Для матриц большего порядка детерминант вычисляется по формуле:

для любого i,

2. n - порядок матрицы;

i – строка (i=1, 2, .... n);

j – столбец (j=1, 2, .... n)

М_ij – минор ij-ого элемента матрицы.

Инверсия

Операция инверсии в матричной алгебре необходима при проведении деления матрицы на матрицу. Инверсия матрицы А обозначается как А^-1. Умножение матрицы на ее инверсию дает матрицу, которая содержит единицы во всех диагональных элементах и нули во всех внедиагональных элементах, т.е.

.

Для получения инверсии матрицы обязательно, чтобы исходная матрица была квадратной и имела ненулевой детерминант.

Инверсия матрицы может быть описана при помощи нахождения кофакторов элементов и детерминанта исходной матрицы.

Технологию вычисления инверсии можно проиллюстрировать следующим примером.

Допустим, нам необходимо получить инверсию матрицы

1. Вычислим кофакторы каждого элемента матрицы.

Для первой строки имеем:

, , , или 20, -46, 18.

Соответственно, кофакторы элементов второй строки равны:

, , , или 10, 13, -19.

Кофакторы элементов третьей строки составляют:

, , , -10, 19, 3.

2. Заменим элементы исходной матрицы их кофакторами:

.

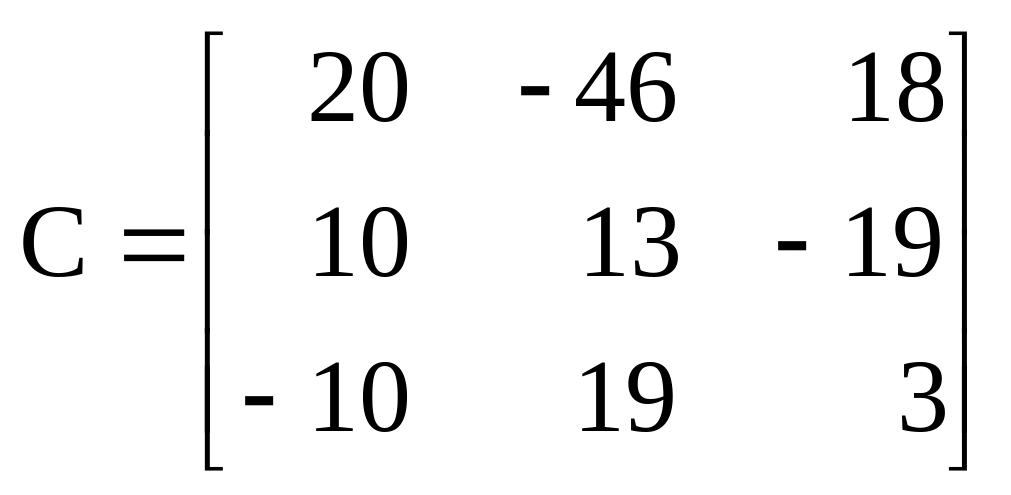3. Транспонируем матрицу кофакторов:

.

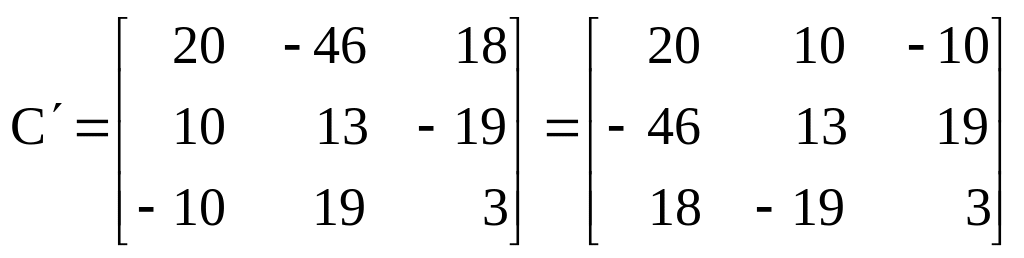4. Умножим транспонированную матрицу кофакторов на величину, обратную детерминанту:

.

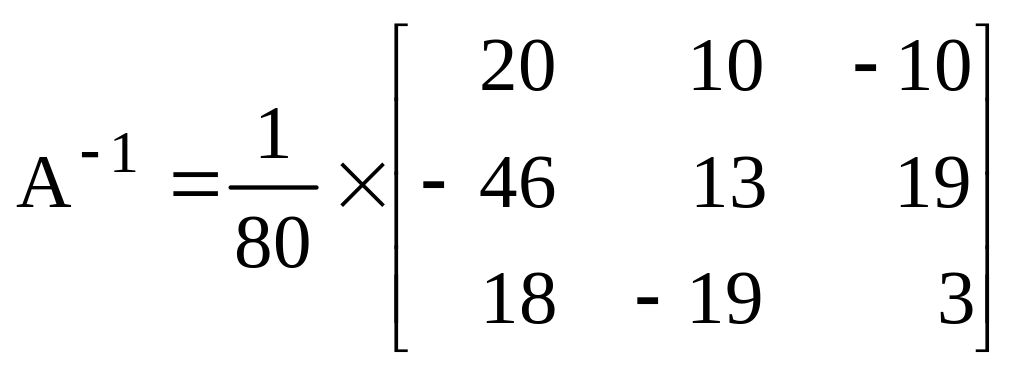Таким образом, матрица А^-1 является инверсией исходной матрицы А. Для проверки правильности проведения операции инверсии произведем умножение инверсии на исходную матрицу А:

.

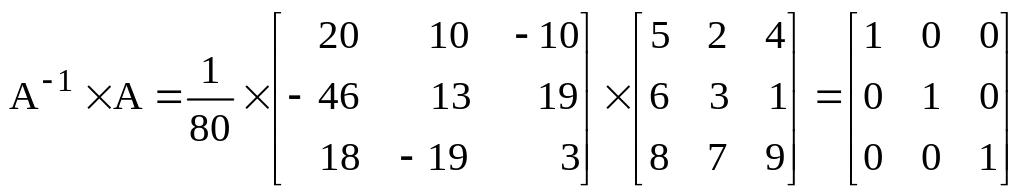Линейная независимость и ранг

Как уже отмечалось, уникальная инверсия матрицы не существует, если детерминант матрицы равен нулю. Детерминант всегда будет равен нулю, если исходная матрица содержит какие-либо строки или колонки, которые являются линейной комбинацией других строк или колонок матрицы.

Например, в матрице 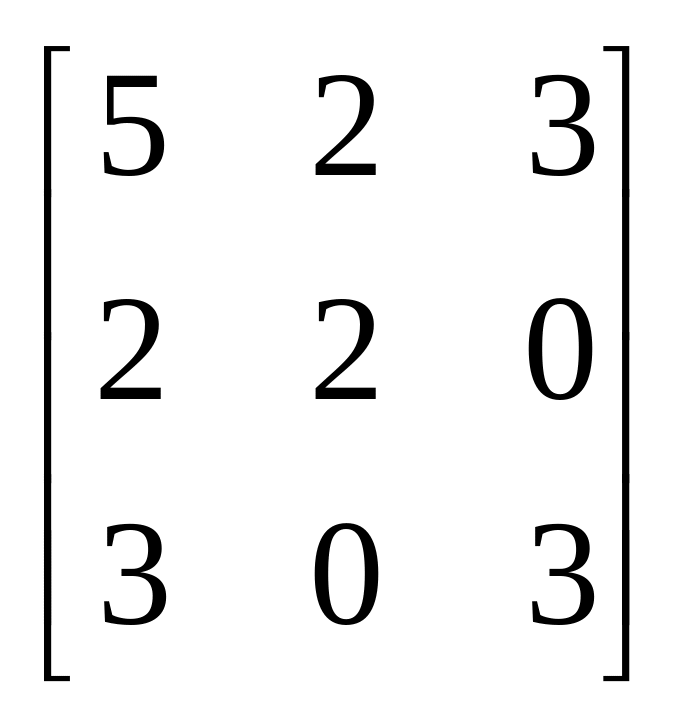первая строка – сумма второй и третьей строк, детерминант этой матрицы равен нулю. Следовательно, уникальная инверсия данной матрицы не существует.

Ранг матрицы представляет собой число линейно независимых строк или колонок матрицы. Очевидно, что для предыдущего примера ранг матрицы равен 2. Если ранг матрицы меньше, чем ее порядок, детерминант исходной матрицы всегда равен нулю, и ее инверсия не существует. Такие матрицы называются матрицами неполного порядка.

Обобщенная инверсия

Несмотря на то, что уникальная инверсия для матрицы неполного порядка не существует, такая матрица обладает обобщенной инверсией.

В этом случае обобщенная инверсия должна удовлетворять следующему равенству:

АА^–А=А,

3. А – исходная матрица;

А^– – обобщенная инверсия.

Обобщенная инверсия не является уникальной, и для матрицы неполного ранга существует множество обобщенных инверсий, удовлетворяющих необходимому равенству. Один из наиболее простых путей нахождения обобщенной инверсии следующий:

• определим субматрицу полного ранга (обозначим её через М);

• инвертируем матрицу М;

• заменим каждый элемент исходной матрицы корреспондирующимся элементом матрицы М^-1;

• заменим все остальные элементы исходной матрицы нулями.

Результат всех предыдущих шагов – обобщенная инверсия исходной матрицы.

Пример. Необходимо найти обобщенную инверсию матрицы

.

Очевидно, что матрица А неполного ранга, поскольку первая строка есть сумма остальных строк матрицы. Следовательно, уникальная инверсия матрицы А не существует (детерминант равен нулю).

Для нахождения обобщенной инверсии:

• сформируем матрицу М полного ранга:

;

• инверсия матрицы М будет равна:

;

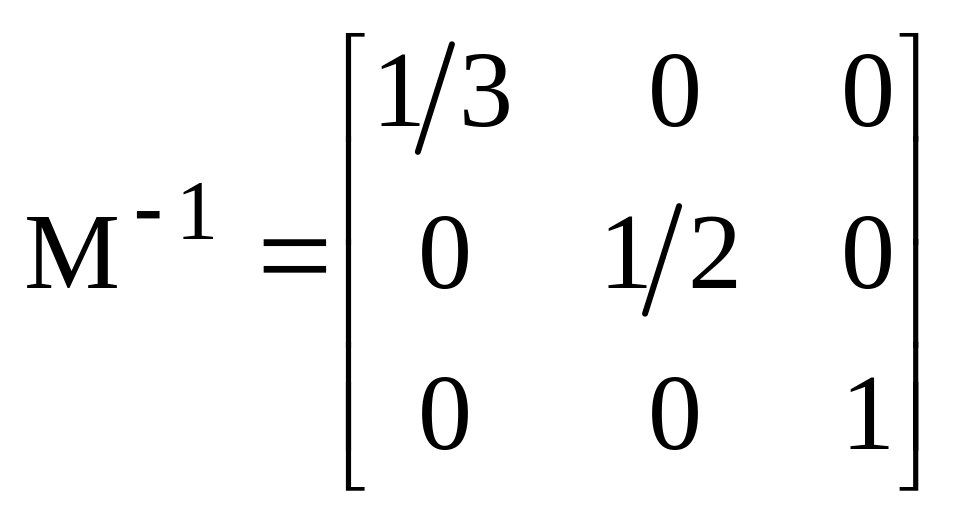• заменив элементы матрицы А соответствующими элементами матрицы М^-1 и добавив нулями элементы первой строки и первой колонки, получаем обобщенную инверсию матрицы А:

.

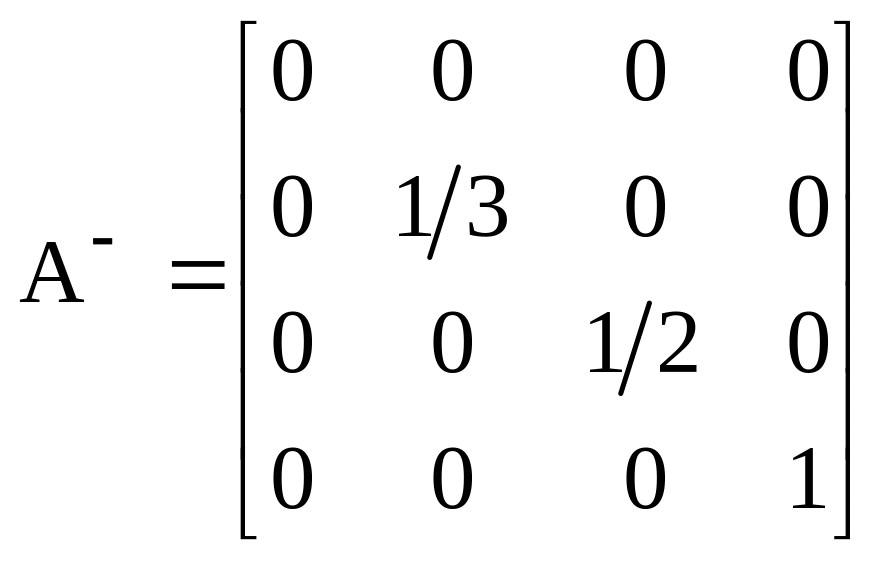Специальные матрицы

Во многих статистических исследованиях используются матрицы, представляющие собой произведение транспонированной матрицы на исходную, т.е. А=Х^–Х.

Такие матрицы всегда симметричны, т.е. любой внедиагональный элемент над диагональю равен противоположному элементу, симметрично расположенному под диагональю. Для таких матриц всегда справедливо равенство:

Х(Х′Х)^–Х′=Х.

Другими словами, несмотря на существование множества обобщенных инверсий матрицы Х′Х, любая обобщенная инверсия, предумноженная на X и умноженная на X′, дает ту же матрицу X.

След матрицы

След матрицы представляет собой сумму диагональных элементов. Для матрицы А порядка n с элементами а_ij след матрицы определяется как:

.

Например, для матрицы

, tr (А) = 1 + 5 + 9 = 15.

Для произведения матриц справедливо равенство

tr (АB) = tr (BA),

что также справедливо для любого количества матриц-сомножителей.