25.Прямые и косвенные методы оценки качества процесса управления.
1) Замена точного уравнения приближенным, за счет отбрасывания несуществующих слагаемых или заменой внешних возмущений на f(t) на более простые.
2) Оценка качества процесса по распределению нулей и полюсов передаточной функции с использованием нормированных диаграмм.
3) Использование интегральных оценок и методов стандартных коэффициентов при приближении искомого процесса х(t) к некоторому эталону.
4) Оценка качества процесса по виду частотной характеристики.
Замена точного уравнения приближенным:
Перемножим, приравняем коэффициенты при одинаковых степенях S:
решим
эти уравнения относительно
. . . . . . .
Переведем в
безразмерную формулу. Для этого разделим
уравнение на
и введем
новую переменную
,
где
,
,
где
,
,
,
Преимущества безразмерной формулы записи в том, что исследование множества систем сводится к исследованию одной системы.
Тогда, зная константы
передаточной функции (
),
(
)
– можно определить
с учетом
зависимости от
.
26. Влияние распределения корней характеристического уравнения на качество передаточного процесса.
Наибольший интерес представляют корни, расположенные ближе к мнимой оси.
– степень колебаний.
Р
φ
Степень устойчивости h физически определяет быстроту затухания процесса. Чем больше h, тем быстрее затухание. Но h не отображает периодичность процесса регулирования, следовательно поэтому водят в рассмотрение – расстояние корня до вещественной оси. Если ближний к мнимой оси корень комплексный, то угол образованный наклонными линиями, характеризует степень колебательности.
Наиболее общий вид определяется степенью устойчивости h – состоит в построении смешенного уровня, нахождении его характеристического уравнения и отыскании его корней.
Пусть дано
характеристическое уравнение
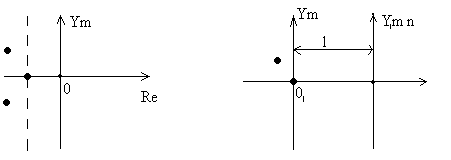
Выполнен переход
к новой переменной Z
по схеме. На плоскости корней р будем
перемещать ОУ, пока она не совпадет с
ординатой ближайшего к мнимой оси корня.
В этом случае появляется некоторый
параметр
, который
характеризует степень устойчивости.
Новое характеристическое уравнение:
Если
,
то смещенное уравнение будет иметь
корень на мнимой осе.
Е
сли
для уравнения (**) применить критерий
Гурвица, то при
– вещественном нулевом корне,
,
а при комплексном
О пределение степени устойчивости сводится к отысканию минимального положительно или вещественного корня для уравнения
Через h
и
можно определить:
и
.
27. Интегральные оценки
Дают общую оценку быстроты затухания и отклонения регулирующей величины.
x(t)
+
+ 
_
t
Критерий
обладает недостатком – он представляет
из себя сумму S
криволинейных трапеций, как с
положительными, так и с отрицательными
сторонами.
Дает хорошие
результаты для монотонных процессов,
иначе используют
:
- вычисление сложно,
как в аналит. так и в мат.
Переходят к третьему критерию:
x(t) + Минус: использует много энергетики
+
+
_
t
минимизируем скорость
x(t)
попадание
на траекторию
более плавное
t
Минусом интегральных
оценок является то, что не чем не
ограничивается форма гривой переходного
процесса. Может оказаться, что совершенно
различные по форме процессы имеют одно
и тоже значение квадратичной оценки
(
).