16. Критерий устойчивости Гурвица и Рауcа.

- определитель Гурвица

Критерий Гурвица: Для устойчивости замкнутой САУ необходимо и достаточно, чтобы определитель Гурвица и все его миноры были положительными при

1) Уравнение 1-го порядка: . Критерий Гурвица: , т.е. достаточно положительности коэф-тов характеристического уравнения.

2) Уравнение 2-го порядка . Критерий Гурвица:

. Тоже достаточно положительности коэф-тов.

3) Уравнение 3-го порядка

Нужно еще выполнение условия . Недостаток: Усложнение вычислений при росте степени.

Критерий Рауса: для устойчивости системы необходимо, чтобы все элементы первого столбца таблицы Рауса были положительными; при наличии отрицательных элементов система неустойчива; если хотя бы один элемент первого столбца равен нулю – система на границе устойчивости.

Количество строк в таблице Рауса должно быть равно n+1, где n – степень характеристического уравнения

С_i,j=

17. Критерий устойчивости Михайлова.

Критерий Михайлова: для того, чтобы САУ была устойчивой, необходимо и достаточно, чтобы годограф Михайлова, начинаясь на положительной части вещественной оси, при изменении  от 0 до + последовательно в положительном направлении проходил n квадрантов, где n – степень характеристического уравнения системы.

Характер системы определяется левой частью(характеристический полином):

(1) Заменим p=jw, где w – угловая частота колебаний, соответствующих чисто мнимому корню другого характеристического полинома:

Критерий 1: Характеристический полином (1) не будет иметь корней в правой полуплоскости(т.е. положит. веществ. или комплексных с положит. веществ. частью), т.е. система будет устойчива, если полное приращение фазы при изменении w от 0 до ∞ равно , где n – показатель степени полинома. Кривая Михайлова – годограф, который описывает вектор с данными координатами.

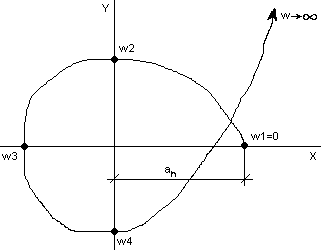
Рассмотрим зависимость между критерием Михайлова и знаками вещественных корней характеристического уравнения при изменении w = [0, ∞)

,

где каждая скобка – комплексное число, а при умножении комплексных чисел аргументы складываются. Результирующий угол:

1) Рассмотрим случай, когда корень p₁ является веществ. и отрицательным: . Тогда этому корню соответствует сомножитель . При w = 0 вещ. часть , а . При увеличении w: , Y – увеличивается, угол поворота .

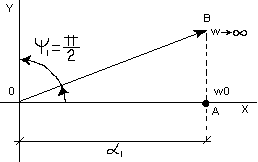
2) p – положительный, ,

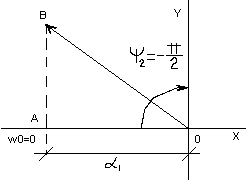
3)

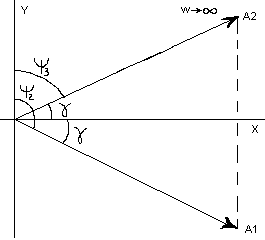
При w = 0 начальное положение 2-х векторов определяется точ. A₁ и A₂. 1-й вектор повернут относительно вещ. оси на , а 2-й вектор повернут на угол против часовой стрелки. Результирующий угол поворота 1-го вектора равен , 2-го . Тогда произведение скобок равно:

4)

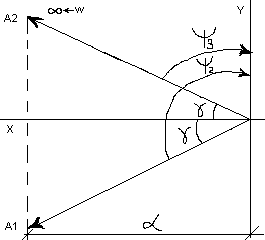
Если характеристическое уравнение имеет l корней с положит. вещ. частью, то каковы бы ни были корни (вещ. или компл.), им соответствует сумма углов поворота, равная .

Остальные (n – l) корней, имеющих отрицат. вещ. части, будут иметь результирующий угол поворота:

Критерий 1: Для линейной системы n-го порядка необходимо и достаточно, чтобы вектор D(jw) , описывающий кривую Михайлова при w = [0, ∞) имел угол поворота . Для устойчивых систем кривая Михайлов имеет плавную спиралевидную форму, причем она уходит в ∞ в квадранте k плоскости, номер которого равен степени характеристического полинома. Для неустойчивых систем характерно нарушение последовательности прохождения квадрантов, вследствие чего угол оказывается меньше, чем .

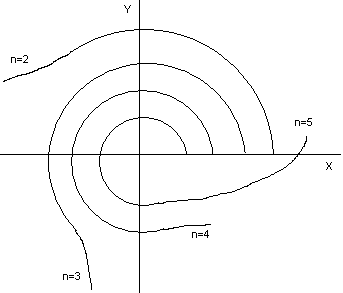
Критерий 2: Для устойчивости системы n-го порядка кривая Михайлова проходит последовательно n квадрантов, из этого следует, что корни уравнений X(w) и Y(w) должны чередоваться.

18. Частотная передаточная функция и частотные характеристики.

Если на вход линейного звена в устойчивом режиме будет подана гармоническая функция: , где – амплитуда, – угловая частота, то на входе будет получена также гармоническая функция той же частоты: , сдвинутую на угол .

Воспользуемся формулой Эйлера: , .

Сигнал на входе: ; сигнал на выходе:

На основании принципа суперпозиции можно рассмотреть прохождение сост-х

Воспользуемся записью:

,

Найдем первую производную:

Подставим в уравнение:

Сократим на , получим:

Выносим за скобки:

Запишем отношение:

;

В более общей постановке: для входного воздействия любого вида частотную передаточную функцию можно представить как отношение входной и выходной величин:

Получим, что ч.п.ф. получается из обычной передаточной функции путем подстановки

Ч.п.ф. – изображение Фурье функции веса:

Для наглядного представления свойств звена используются следующие частотные характеристики:

1. Амплитудно-фазовая частотная характеристика (АФЧХ).

строится в комплексной плоскости, представляет собой геометрическое место точек концов векторов (годограф), соответствующее ч.п.ф. в комплексной форме.

Т.к. может быть (+) и (–), то строится только положительная ветвь, а отрицательная – зеркально отображается.

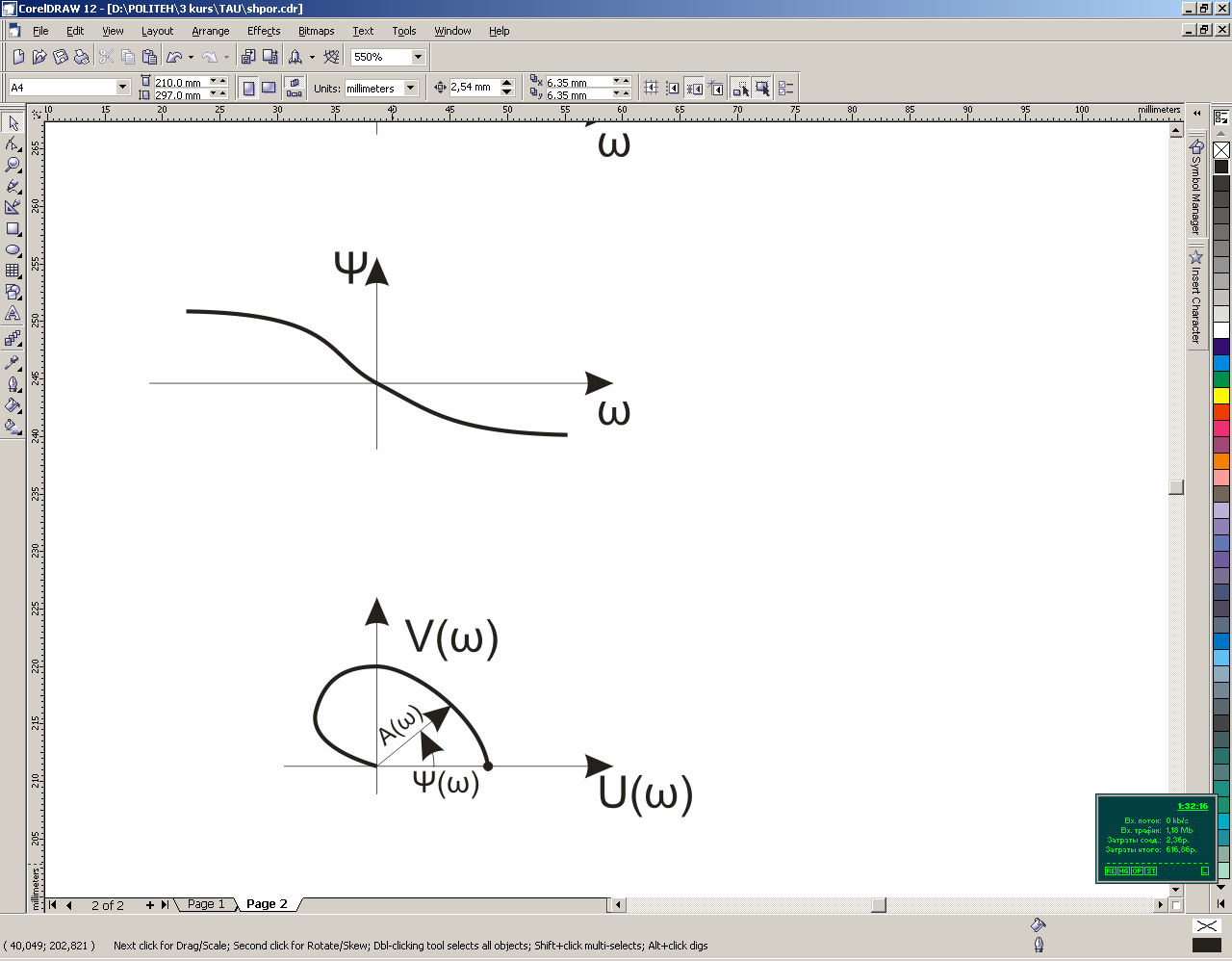
Построение АФФЧХ по вещественным и мнимым частям – трудоемкая работа, проще строить ее, используя полярные координаты при непосредственном вычислении модуля и фазы. В этом случае, зная модуль и фазу, легко вычислить вещественную и мнимую части путем умножения модуля на направл. косинус между вектором и соответствующей осью.

2. АЧХ

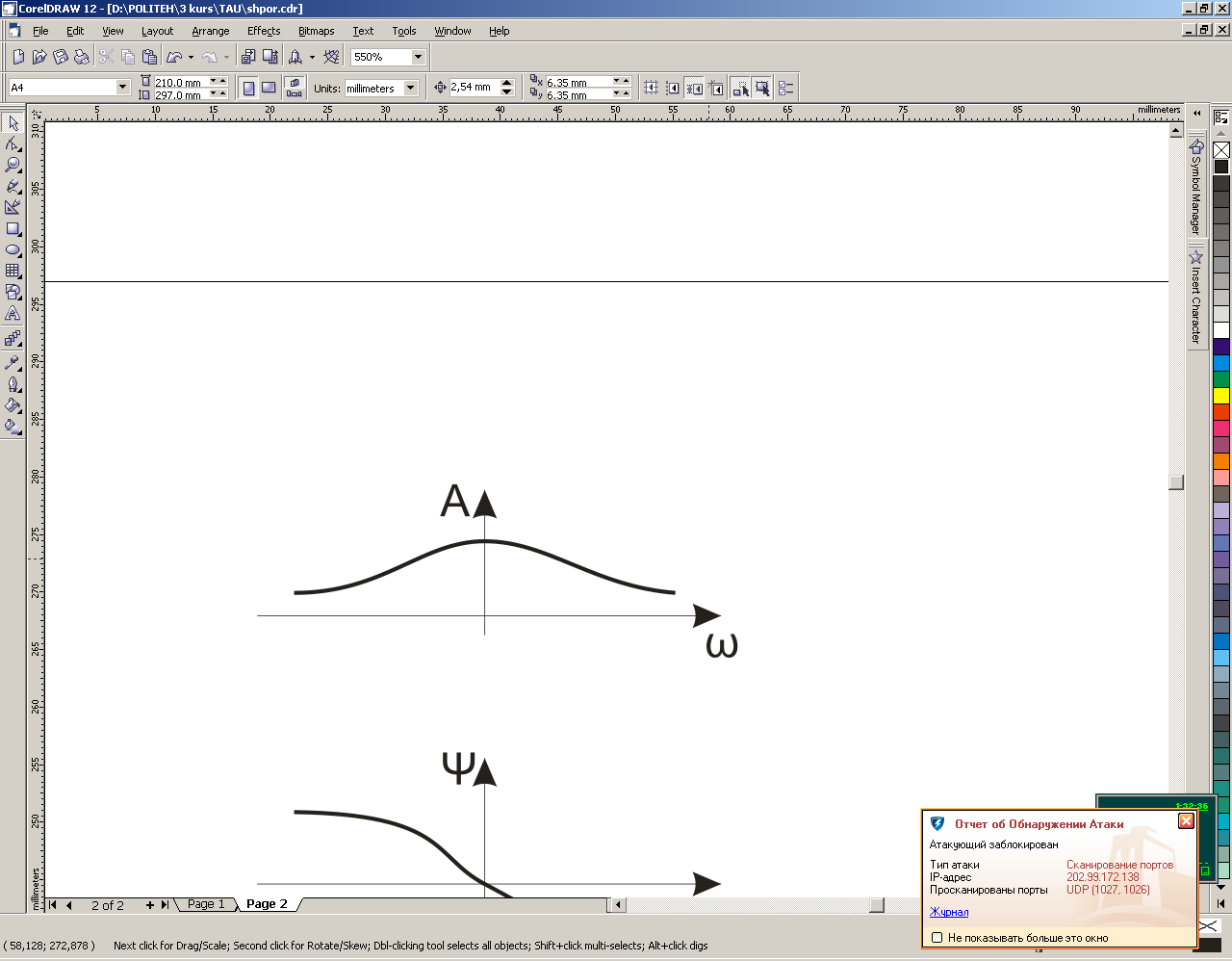
Показывает, как звено пропускает сигнал различной частоты

3. ФЧХ

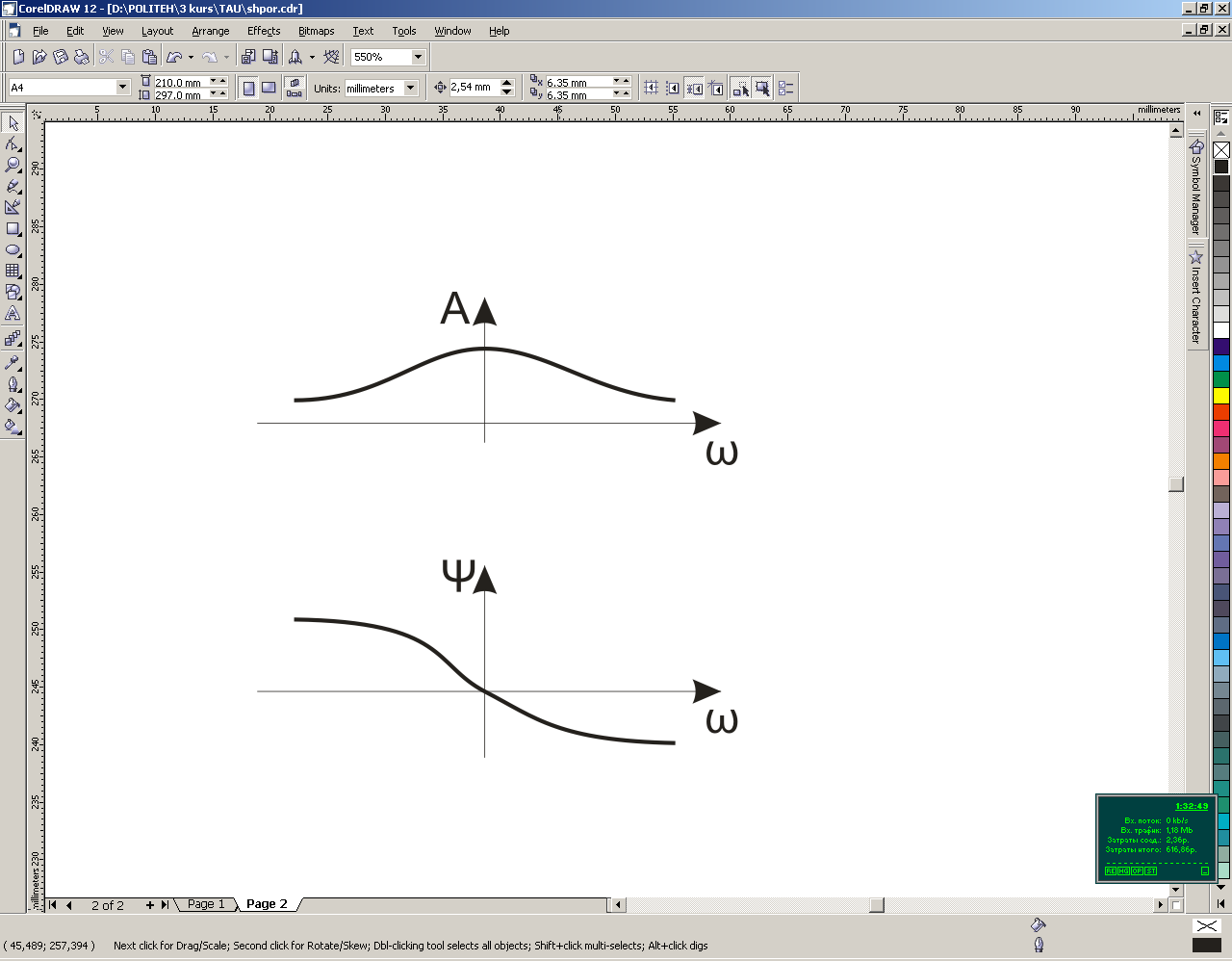
Показывает фазовые сдвиги, вносимые звеном на различных частотах.