Критерий Вышнеградского для систем III порядка:

Для устойчивости системы необходимо и достаточно, чтобы выполнялись условия:

1. a_i > 0

2. a₂a₁ > a₀a₃

Запишем уравнение в безразмерном виде:

p³+A₂p²+A₁p+1=0

Критерий Вышнеградского:

для устойчивости системы необходимо и достаточно: A₁ > 0, A₂ > 0, A₁A₂ > 1

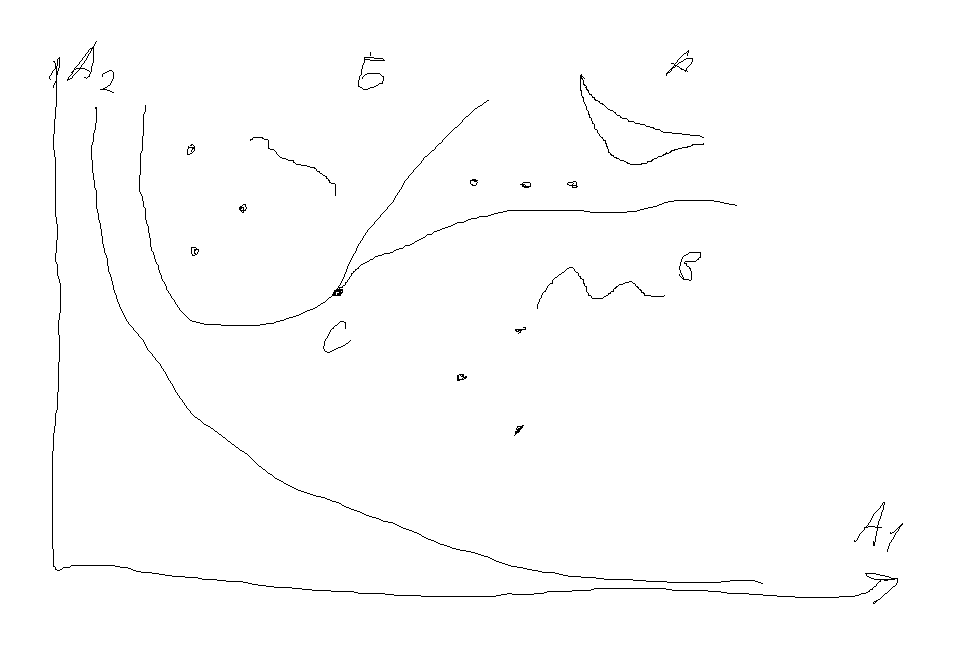
• 3 вещественных корня (A) – апериодический процесс;

• Область (Б) – монотонный процесс, колебательная часть затухает быстрее;

• Область (В) – колебательный процесс, колебательная часть затухает медленнее.

C – точка равенства всех корней. Границе между любыми областями будет соответствовать предельное между двумя распределениями расположение корней.

Билет 27.

Интегральные оценки дают общую информацию о быстроте затухания и величине отклонения регулируемой величины.

, где x(t)=x_пер – x_оп – отклонение регулируемой величины от нового установившегося значения. В устойчивой системе при x0, t∞ интеграл имеет конечную величину. Геометрический смысл – площадь под кривой переходного процесса, записанного в отклонениях.

Не всегда объективен (площади могут быть отрицательными), поэтому зачастую применяют другую оценку:

При управлении желательно минимизировать эти оценки, однако иногда требуется поправка на скорость (не должна быть большой):

Билет 28.

На практике требуется определять характеристики системы при отклонении параметров системы от расчетных. Для оценки этого явления используют функции чувствительности:

, α_j – изменяемый параметр, 0 – функция вычисляется при расчетном α_j.

Исходная функция – функция, все параметры которой соответствуют расчетным (не имеют вариаций), н-р:

.

Варьируемая система – есть вариации параметров:

Дополнительное движение: .

При условии дифференцируемости функций по α_i, возможно разложить дополнительное движение в ряд Тейлора. Для первого приближения получим следующее:

.

При существенной нелинейности используется второе приближение в ряду Тейлора.

Дифференцирование исходных уравнений ведет к получению уравнений чувствительности, решение которых позволяет найти u_i,j:

Удобно использовать передаточные функции:

Функция чувствительности передаточной функции:

Билет 29.

Системы с запаздыванием – системы, имеющие в одном или нескольких звеньях запаздывание во времени начала изменения выходной величины после изменения входной на величину τ.

Уравнение динамики звена с запаздыванием можно разбить на 2:

1. Q(p)x₂=R(p)x₁*

2. x₁*(t)=x₁(t-τ)

Реальное звено с запаздыванием можно приближенно описать, используя разложение в ряд:

, p – оператор дифференцирования.

W(p)=e^-τp – передаточная функция звена чистого дифференцирования.

Тогда:

Q(p)x₂ = R(p) e^-τp x_1.

Частотная передаточная функция с запаздыванием:

W(iw)=W₀(iw)e^-iwτ = A₀(w)e^i(u(w)-τw).