3 Вывод 1закона через энтальпию, через энтропию

Энтальпия

Ранее была приведена так называемая интегральная форма записи первого закона (1), согласно которой для произвольного количества вещест

Для 1 кг вещества:

Дифференциальная форма записи уравнения первого закона при анализе термодинамических процессов часто оказывается более удобной. Уравнение первого закона термодинамики можно представить в другом виде. К выражению

прибавим и вычтем слагаемое Vdp: Последнее слагаемое представляет собой элементарную располагаемую работу. Функцию измеряемую в Дж, в термодинамике называют энтальпией. Энтальпия, отнесенная к 1 кг называется удельной энтальпией. Входящие в выражение (19) величины u, p, υ являются параметрами состояния, поэтому и сама энтальпия также будет параметром (функцией) состояния. Тогда аналитические выражения для первого закона примут вид: Записывая последнее выражение для изобарного процесса p=const, получаем: т.е. изменение энтальпии численно равно количеству теплоты, подводимому к системе в изобарном процессе. Тогда можно записать: В заключение следует отметить, что общее уравнение первого закона термодинамики

Энтропия

Одним из функций состояния термодинамической системы является энтропия. Энтропией называется величина определяемая выражением:dS = dQ / T. [Дж/К] (3.1)или для удельной энтропии:ds = dq / T. [Дж/(кг·К)] (3.2)

Энтропия есть однозначная функция состояния тела, принимающая для каждого состояния вполне определенное значение. Она является экстенсивным (зависит от массы вещества) параметром состояния и в любом термодинамическом процессе полностью определяется начальным и конечным состоянием тела и не зависит от пути протекания процесса.

Энтропию можно определить как функцию основных параметров состояния:S = f1(P,V) ; S = f2(P,T) ; S = f3(V,T) ; (3.3)или для удельной энтропии:s = f1(P,υ) ; s = f2(P,T) ; S = f3(υ,T) ; (3.4)

Так как энтропия не зависит от вида процесса и определяется начальными и конечными состояниями рабочего тела, то находят только его изменение в данном процессе, которые можно найти по следующим уравнениям:

Ds = cv·ln(T2/T1) + R·ln(υ 2/υ 1) ; (3.5)

Ds = cp·ln(T2/T1) - R·ln(P2/P1) ; (3.6)

Ds = cv·ln(Р2/Р1) + cр·ln(υ 2/υ 1) . (3.7)

Если энтропия системы возрастает (Ds > 0), то системе подводится тепло.

Если энтропия системы уменьшается (Ds < 0), то системе отводится тепло.

Если энтропия системы не изменяется (Ds = 0, s = Const), то системе не подводится и не отводится тепло (адиабатный процесс).

5.Исследование изохорного процесса, изобарного, изотермического, адиабатного, политропного.

1). Изохорный процесс (Рис.4.1).

n = Const , n 2 = n 1. (4.10)

Уравнение состояния процесса:

P2 / P1 = T2 / T1. (4.11)

Так как υ 2 = υ 1, то l = 0 и уравнение 1-го закона т/д имеет вид:

q = Du = = сv·(t2 - t1); (4.12)

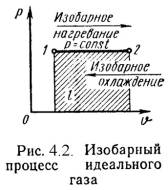
2). Изобарный процесс (Рис.4.2).

P = Const , P2 = P1

Уравнение состояния процесса:

n 2 /n 1 = T2 / T1 , (4.13)

Работа этого процесса:

l = P·(n 2 - n 1). (4.14)

Уравнение 1-го закона т/д имеет вид:

q = Du + l = ср·(t2 - t1); (4.15)

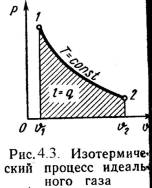
3). Изотермический процесс (Рис.4.3).

Т = Const , Т2 = Т1

Уравнение состояния:

P1 / P2 = n 2 / n 1 , (4.16)

Так как Т2 = Т1, то Du = 0 и уравнение 1-го закона т/д будет иметь вид:

q = l = R·T·ln(n 2/n 1), (4.17)

или q = l = R·T·ln(P1/P2), (4.18)

где R = Rh/ h – газовая постоянная [Дж/(кг·К)].

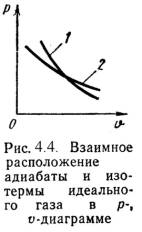
4). Адиабатный процесс (Рис.4.4).

В данном процессе не подводится и не отводится тепло, т.е. q =0.

Уравнение состояния:

P· nl = Const, (4.19)

где l = cp / cv – показатель адиабаты.

Уравнение 1-го закона т/д будет иметь вид:

l = -Du = = -сv·(t2 – t1) = сv·(t1 – t2), (4.20)

или

l = R·(T1 – T2) / (l -1); (4.21)

l = R·T1·[1 – (n 1/ n 2)l -1] /(l – 1); (4.22)

l = R·T2·[1 – (P2/P1) (l -1)/ l] /(l – 1). (4.23)

5)Политропный процесс — термодинамический процесс, во время которого удельная теплоёмкость газа остаётся неизменной. Предельными частными явлениями политропного процесса являются изотермический процесс и адиабатный процесс. В случае идеального газа изобарный процесс и изохорный процесс также являются политропическими.

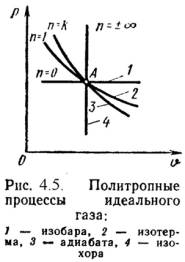
Для идеального газа уравнение политропы может быть записано в виде