6. По семейству выходных характеристик полевого транзистора построить стоко-затворные характеристики. Составить таблицу основных параметров полевого транзистора.

По данным таблицы 10 заданного варианта (таблица 2) строится семейство выходных характеристик полевого транзистора. Стоко-затворная характеристика представляет собой зависимость тока стока I_c от напряжения на затворе U_з. Параметром стоко-затворной характеристики, определяющим семейство этих характеристик, является напряжение на стоке U_си. Последовательность построения стоко-затворной характеристики следующая. На семействе выходных характеристик выбирается первое значение напряжения на стоке (U_си1) в области начала насыщения ВАХ при нулевом напряжении на затворе. Для этого напряжения проводится перпендикуляр и в точках его пересечения с вольт-амперными характеристиками находится ток стока (I_c) и напряжение на затворе (U_з). Эти координаты заносятся в таблицу и по ним строится первая стоко-затворная характеристика. Затем выбирается второе значение напряжения на сто­ке, близкое к максимальному значению, и при этом значении восстанавливается перпендикуляр. Все остальные действия аналогичны рассмотренным при по­строении первой характеристики. Построенные стоко-затворные характеристики необходимо продлить до пересечения с осью напряжений на затворе. Точка пересечения даст значение напряжения отсечки. Сравните это значение напряжения отсечки со значением напряжения отсечки в справочных данных (рисунок П.9).

Приложение

к контрольной работе №2

Рисунок П.1 – ВАХ диода для

определения R_ст и R_дин

Рисунок П.2 – Зависимос

Рис. П.1. ВАХ диода для

определения R_ст и R_дин

Рис. П.2. Зависимость R_ст и R_дин

от U

Рис.П.3. ВАХ стабилитрона. Рис.П.4. ВАХ для двух стабилитронов,

включённых последовательно согласно.

МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ВЫПОЛНЕНИЮ

КУРСОВОЙ РАБОТЫ

ВВЕДЕНИЕ

МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ВЫПОЛНЕНИЮ

КУРСОВОЙ РАБОТЫ

ВВЕДЕНИЕ

Целью курсовой работы является выработка практических навыков анализа радиотехнических цепей второго порядка. Цепями второго порядка называются цепи, описывающиеся дифференциальными уравнениями второго порядка. Эти цепи очень широко распространены в радиотехнических устройствах (колебательные контура одиночные и связанные, реактивные фильтры и т.д.). Наличие навыков анализа таких цепей совершенно необходимо, как для дальнейшего обучения по выбранной специальности, так и для успешной рабо­ты в области радиоэлектроники.

При выполнении курсовой работы рекомендуется использовать следующую литературу:

1. Станевко В.Н. Основы теории цепей: Учебное пособие. Часть Рыбинск, РГАТА имени П.А.Соловьёва, 2009 – 172с.

2. Анализ радиотехнических цепей. Методические указания к курсовому и дипломному проектированию / РАТИ каф. КиПРА; Сост. В.Н. Станевко - Рыбинск, 1989. 40с.

3. Карлашук В.И. Электронная лаборатория на IBM PC: Программа Electronics Workbench и ее применение. - М.: Солон-Р, 2001. -726с.

ЗАДАНИЕ НА КУРСОВУЮ РАБОТУ

1. Выполнить электрический расчёт заданной цепи при гармоническом входном воздействии:

1.1 Определить вид и параметры характеристического сопротивления нагрузки, удовлетворяющей условию , подключаемую к выводам исходной схемы.

1.2 Рассчитать заданную электрическую цепь с учётом п.1.1. при гармоническом входном сигнале:

.

1.3 Оценить точность расчёта методом баланса мощностей. Погрешность расчёта не должна превышать 1%.

2. Выполнить частотный анализ цепи:

2.1 Найти комплексный коэффициент передачи по напряжению.

2.2 Определить аналитическое выражение и построить АЧХ и ФЧХ.

2.3 Определить по АЧХ полосу пропускания.

3. Выполнить анализ переходного процесса при ступенчатом входном воздействии:

,

где – единичная ступенчатая функция.

3.1 Получить аналитическое выражение, описывающее переходный процесс.

3.2 Построить график переходного процесса.

3.3 По графику (п. 3.2) определить время переходного процесса.

4. С помощью программы EWB провести анализ АЧХ и переходного процесса для всех заданных значений резисторов (смотреть исходные данные). Дать объяснение влияния величин заданных резисторов на вид АЧХ и длительность переходного процесса.

При выполнении п.2.2 и п.3.2 наличие таблиц значений для графиков обязательно.

Исходные данные:

f = 5·10³ Гц; R₁ = 2 Ом; R₂ = 2000 Ом;

С = 1·10^-6 Ф; L = 1·10^-3 Гн; U_m = 10 В.

При выполнении п.4 резистору задавать следующие значения:

= 20 Ом; 30 Ом; 40 Ом.

Примечание: У каждого студента своя схема для расчёта. Схему для расчёта определяет преподаватель из ниже указанных вариантов схем.

ВАРИАНТЫ СХЕМ

ПОЯСНЕНИЯ К ВЫПОЛНЕНИЮ КУРСОВОЙ РАБОТЫ

1. В п. 1.1 задания сказано определить вид и параметры характеристического сопротивления нагрузки, удовлетворяющей условию , подключаемую к выводам исходной схемы. Это значит, что в место указанной на схеме R_Н, подключённой к выводам 2 – 2`, должна быть подключена согласованная нагрузка (см. раздел программы 5.Четырёхполюсники, Характеристические параметры четырёхполюсника -входные и выходные характеристические сопротивления четырёхполюсника).

После определения и её составляющих элементов, найденная нагрузка подключается к схеме и выполняется расчёт всей схемы любым известным методом.

Точность расчёта определяется методом баланса мощностей. Погрешность расчёта не должна превышать 1%.

2. При частотном анализе цепи вначале находится комплексный коэффициент передачи по напряжению. Для этого нужно рассчитать напряжение на в комплексной форме и взять его отношение к входному напряжению, представленному также в комплексной форме. Для определения напряжения на нагрузке можно использовать любой известный метод. Однако, из всех методов рекомендуется применить расчёт методом эквивалентного источника напряжения .

Модуль комплексного коэффициента передачи будет являться амплитудно-частотной характеристикой (АЧХ), а фаза комплексного коэффициента передачи будет являться фазо-частотной характеристикой (ФЧХ). Задавая конкретные значения частоты и подставляя их в выражения для АЧХ и ФЧХ, определяются соответствующие им значения АЧХ и ФЧХ. По результатам расчетов строятся графики АЧХ и ФЧХ. С помощью построенного графика АЧХ определяется полоса пропускания.

3. Анализ переходного процесса в цепи начинается с представления схемы в операторной форме и нахождения напряжения на нагрузке в операторной форме. В выражение для напряжения на нагрузке подставляется операторное представление ступенчатого входного воздействия. Полученное соотношение и будет являться аналитическим выражением, описывающее переходный процесс в заданной цепи в операторной форме. Далее необходимо перейти от изображения к оригиналу. Для этого с помощью обратного преобразования Лапласа или теорем разложения переходят от операторного представления напряжения на нагрузке к выражению этого напряжения в функции времени. Подставляя конкретные значения времени в это выражение, находятся значения напряжения на. По этим значениям строится график переходного процесса. С помощью графика переходного процесса определяется время переходного процесса в цепи.

4. С помощью пакета программы Electronics Workbench на компьютере представить заданный вариант схемы с соответствующими параметрами. Подключить к схеме необходимые приборы и снять АЧХ и переходный процесс для вашего варианта задания при различных значениях R₁. Полученные графики АЧХ и переходных процессов проанализировать – определить полосы пропускания и время переходных процессов. По результатам анализа установить как влияет изменение величины R₁ на величину полосы пропускания, времени переходного процесса и добротность схема.

В заключении необходимо отметить, что в курсовой работе должны даваться пояснения всем действиям и должны быть представлены все основные промежуточные выкладки.

Пример ВЫПОЛНЕНИЯ КУРСОВОЙ РАБОТЫ

ЗАДАНИЕ НА КУРСОВУЮ РАБОТУ

Вариант 0

Выполнение курсовой работы начинается с задания на курсовую работу, которое указано выше. В примере будет рассмотрена схема, показанная на рис.1

Исходные данные

f = 1·10³ Гц; R₁ = 10 Ом; R₂ = 100 Ом;

С = 5·10^-6 Ф; L = 5·10^-3 Гн; U_m = 10 В.

1.Электрический расчет заданной цепи при гармоническом входном воздействии.

В соответствии с заданием электрический расчет состоит из двух этапов - определение вида и параметров характеристического сопротивления нагрузки и расчета цепи с найденной нагрузкой.

Для дальнейшего расчета понадобятся значения следующих величин:

.

1.1. Определение вида и параметров характеристического сопротивления нагрузки.

В соответствии с заданием нагрузкой цепи должно являться его характеристическое сопротивление:

(1)

В соответствии с теорией четырехполюсников] характеристическое сопротивление может быть определенно через параметры холосто хода и короткого замыкания по следующей формуле:

(2)

Исходя из (2) видно, что для определения достаточно определить только два параметра - и .

Сопротивление - это сопротивление между выводами схемы при разомкнутых выводах (рис.2).

Из рис.2 видно, что определяется по формуле:

Представляем численные значения в эту формулу и, после очевидных преобразований, находим:

(3)

Сопротивление это сопротивление между выводами при коротком замыкании между выводами . Эта схема представлена на рис.3.

Из схемы рис.3 видно, что определяется по формуле:

После подстановки в эту формулу численных значений и очевидных преобразований, находим:

(4)

При вычислениях рекомендуется уменьшать численные значения выражений путем их взаимного сокращения. Так при вычислении дроби в целесообразно сделать сокращение числителя и знаменателя на .

Найденные значения и подставляем в формулу (2):

.

Исходя из (1), запишем:

(5)

Из (5) получаем:

(6).

Реактивная (мнимая) составляющая может быть или индуктивностью или конденсатором. Как известно, индуктивное сопротивление имеет положительное значение, а емкостное сопротивление имеет отрицательное значение. Наличие минуса в реактивной составляющей сопротивления (5) говорит о том, что реактивной составляющей согласованной нагрузки является конденсатор. Обозначим реактивную составляющую сопротивления через . Найдем величину конденсатора нагрузки.

.

Из последнего соотношения находим.

.

Итак, согласованная нагрузка представляет цепь из последовательно соединённых резистора и конденсатора (рис.4).

Элементы цепи нагрузки имеют следующие значения:

, , .

1.2Электрический расчет цепи с учетом найденной нагрузки.

Схема цепи в комплексной форме с учетом найденной нагрузки представлена на рис.5.

Электрический расчет схемы на рис.5 можно выполнить следующими тремя методами – методом эквивалентного преобразования, с помощью законов Кирхгофа и методом контурных токов. Выбор метода расчёта произволен. Чтобы иметь возможность сравнить эти методы ниже приводятся расчеты каждым из названных методов.

1.2.1. Расчет методом эквивалентного преобразования.

Прежде чем приступить к расчёту названным методом, рассмотрим основные положения этого метода и последовательность расчёта этим методом в соответствии с .

Основная идея метода состоит в том, что электрическая цепь последовательно преобразуется ("сворачивается") до одного эквивалентного элемента, и определяется входной ток. Затем осуществляется постепенное возвращение к исходной схеме ("разворачивание") с последовательным определением токов и напряжений.

Последовательность расчёта:

1. Расставляются условно–положительные направления токов и напряжений.

2. Поэтапно эквивалентно преобразуются участки цепи. При этом на каждом этапе во вновь полученной после преобразования схеме расставляются токи и напряжения.

3. В результате эквивалентного преобразования определяется величина эквивалентного сопротивления цепи.

4. Определяется входной ток цепи с помощью закона Ома.

5. Поэтапно возвращаясь к исходной схеме, последовательно находятся все токи и напряжения.

Для выполнения расчета методом эквивалентного преобразования представим исходную схему в комплексной форме и расставим условно- положительные направления токов и напряжений (рис.6).

Между параллельно соединенными элементами и находиться перемычка. Перемычка не рассматривается как самостоятельная ветвь, т.к. в ней нет элементов, поэтому ток в ней не вычисляется и не показан.

Первое эквивалентное преобразование целесообразно выполнить по объединению и , результат обозначим как (рис.7).

Выразим :

.

Второй этап эквивалентного преобразования состоит в объединении и , результат обозначим как (рис.8).

Определим :

.

Третий этап эквивалентного преобразования состоит в объединении трех параллельно соединенных элементов , и и результат объединения обозначим как . В принципе на этом этапе можно определить полное сопротивление между выводами , просуммировав с результатом эквивалентного преобразования параллельно соединённых названных трё1х элементов схемы. Однако, это приведёт к пропуску одного этапа эквивалентного преобразования, что вызовет затруднение в расчёте при обратном переходе. Итак, объединив параллельно соединённые элементы, схема принимает вид, представленный на рис.9.

Эквивалентное сопротивление определяется по формуле:

(7)

При вычислении (7) выражения числителя и знаменателя будут принимать большие численные значения. Рекомендуется выполнить сокращения числителя и знаменателя на 10³, что делает более обозримым процесс вычисления. Итак, подставляя численные значения в (7) и, выполняя очевидные преобразования, получим:

.

Входное сопротивление цепи обозначим через и оно будет равно:

Подставляя численные значения и выполняя очевидные преобразования, находим :

Теперь можно определить входной ток . Входное напряжение в комплексной форме имеет вид:

Частоту в выражениях для электрических величин (токи и напряжения) принято не обозначать конкретным числом. Пользуясь законом Ома, находим:

.

В соответствии с требованиями последовательности расчёта данным методом возвращаемся к схеме на рис.9 и по закону Ома находим напряжения и :

(8)

В процессе предыдущих вычислений могла иметь место ошибка, которая будет проявляться в последующих вычислениях и обнаружится только на этапе определения погрешности всего расчёта. В случае, если погрешность будет больше допустимой, придётся проверять все расчёты с самого начала. Выяснить правильно ли идёт расчёт можно в процессе расчёта. Это можно сделать уже сейчас двумя способами. Первый состоит в следующем. Для схемы рис.9 определены и . В соответствии с вторым законом Кирхгофа должно выполняться равенство:

.

Входное напряжение известно:

.

Найдём сумму напряжений и , для этого, пользуясь результатами решений (8), алгебраически суммируем косинусные и синусные составляющие и находим:

.

Видно, что равенство для второго закона Кирхгофа выполняется с большой точностью.

Второй способ оценки правильности расчёта состоит в определении погрешности расчёта на данном этапе расчёта методом баланса мощностей .

Для определения потребляемой схемой мощности необходимо знать все её диссипативные элементы. Одним из них является резистор . Комплексное

сопротивление содержит диссипативную и реактивную составляющие, которые обозначим соответственно, как и :

.

Из этого соотношения видно, что диссипативная составляющая равна:

.

Тогда мощность, потребляемая всей схемой, будет определяться из выражения:

Вт.

Мощность источника определяется из выражения:

Вт.

Погрешность расчёта определяется по формуле:

.

Подставляем численные значения и находим, что погрешность расчёта составляет

.

Оба способа оценки точности расчёта показали, что расчёт выполняется с малой погрешностью и можно с уверенностью продолжать расчёт. Поэтапная проверка точности расчёта позволяет найти этап, где допущена ошибка и устранить её.

Продолжим расчёт. Для этого перейдём к схеме на рис.8. Из схемы видно, что

. (9)

Учитывая (9) и (8),определяем токи в параллельных ветвях:

, ,

.

На этом этапе так же можно проверить на сколько точно ведётся расчёт. Одним из методов, с помощью которого можно это выполнить является проверка выполнения первого закона Кирхгофа. В соответствии с ним должно выполняться равенство:

.

Проверить выполнение этого равенства можно построением прикидочной векторной диаграммы. Выполненный анализ показал, что на последнем этапе расчета ошибок не было. Читателю предлагается выполнить это самостоятельно.

Возвращаемся к схеме на рис.7 и определяем напряжения на конденсаторе и на нагрузке .

Так как сопротивление нагрузки состоит из двух элементов (рис.6), то необходимо определить напряжения на каждом элементе цепи нагрузки:

Оценка погрешности расчета.

В соответствии с заданием погрешность расчета будет оцениваться методом баланса мощностей. В соответствии с этим методом погрешность расчета определяется по формуле:

,

где Р_ист – мощность, выделяемая источником,

Р_н – суммарная мощность, потребляемая всеми диссипативными элементами.

Эти мощности определяются по формулам:

,

где - фаза входного тока .

Подставляем численные значения в эти формулы, находим значения мощностей:

Вт

Вт

Подставляем найденные значения мощностей в формулу для определения погрешности:

Полученная погрешность удовлетворяет требованию задания.

2 Частотный анализ цепи

2.1 Определение комплексного коэффициента передачи цепи по напряжению.

Для решения этой задачи необходимо найти комплексным коэффициентом передачи по напряжению:

. (10)

Из этого соотношения следует, что нужно найти напряжение на нагрузке в комплексной форме и разделить его на входное напряжение, представленное в комплексной форме. На рис.10 представлена исходная схема.

Для определения напряжения на нагрузке можно применить любой из ранее используемых методов. Однако, исходя из того, что в данном случае интерес представляет только напряжение на нагрузке, поэтому целесообразно применить тот метод, который позволит определить сразу ток в цепи нагрузки. Из выше приведённых методов это позволяют сделать расчёт с помощью законов Кирхгофа и расчёт с помощью контурных токов. В расчёте с помощью законов Кирхгофа в исходной системе уравнений путём последовательного исключения можно сразу получить решение для тока цепи нагрузки. Далее, по закону Ома, определяется напряжение на нагрузке. Совершенно аналогично можно поступить, пользуясь расчётом с помощью контурных токов. Здесь также путём последовательного исключения в исходных уравнениях достаточно найти только тот контурный ток, который протекает по цепи нагрузки. Этот ток равен току цепи нагрузки и, как и в предыдущем случае, по закону Ома определяется напряжение на нагрузке. Из рассмотренных двух методов предпочтение можно отдать второму, т.к. в расчёте контурными токами число исходных уравнений меньше, чем при расчёте по законам Кирхгофа, а значит, он менее трудоёмок.

Однако есть метод, который рекомендуется применять в тех случаях, когда необходимо определить ток только в одной ветви схема. Это метод эквивалентного источника напряженния. Воспользуемся этим методом для определения тока в цепи нагрузки. Предварительно вспомним последовательность расчёта этим методом .

Последовательность расчета:

1. Отсоединить от схемы интересующую ветвь. Клеммы, к которым подсоединена эта ветвь, обозначить через .

2. Рассчитать оставшуюся часть цепи и определить напряжение на клеммах ( ).

3. В оставшейся части цепи заменить источники ЭДС перемычкой или резистором, сопротивление которого равно внутреннему сопротивлению источника ЭДС.

4. Определить сопротивление этой цепи относительно клемм , которое обозначим .

5. Оставшуюся часть цепи заменить последовательно соединёнными источником ЭДС с напряжением и резистором с сопротивлением . Эту цепь подсоединить к клеммам .

6. К клеммам подсоединить интересующую ветвь и определить ток, протекающий через нее.

Представим исходную схему в комплексной форме (рис.11).

Далее, в соответствии с последовательностью расчёта, отсоединяем от клемм цепь нагрузки (рис.12).

В схеме без нагрузки (рис.12) необходимо определить напряжение между выводами . Так как выводы разомкнуты, то через конденсатор не протекает ток, а значит, на нём не падает напряжение. Тогда очевидно, что напряжение на выводах равно напряжению, прикладываемому к параллельно соединённым резистору и катушки индуктивности . Падение напряжения на этих элементах можно определить методом эквивалентного преобразования и будет определяться по формуле:

. (11)

Далее, в соответствии с пунктами 3 и 4 последовательности расчёта, замыкаем выводы (рис.13) и определяем сопротивление между выводами , которое обозначим как .

Сопротивление определяется по формуле:

. (12)

В соответствии с требованиями пунктов 5 и 6 последовательности расчёта составляем схему с эквивалентным генератором, которая представлена на рис.14.

В соответствии с этой схемой ток в цепи нагрузки определяется по формуле:

. (13)

Напряжение на нагрузке определяем по закону Ома:

. (14)

Комплексный коэффициент передачи по напряжению определяется по формуле (10). С учётом (14) комплексный коэффициент передачи, после некоторых преобразований, принимает вид:

. (15)

Теперь подставляем в (15) численные значения. Комплексный коэффициент передачи является частотно зависимой функцией, т.е. зависит от частоты входного сигнала. Поэтому в (15) численное значение частоты не ставится. В (15) сопротивления конденсатора, индуктивности и нагрузки необходимо подставлять в следующем виде:

.

.

.

В результате выполненных подстановок и необходимых преобразований комплексный коэффициент передачи принимает вид:

. (16)

2.2 Определение амплитудно-частотной и фазо-частотной характеристик

2.2.1Определение амплитудно-частотной характеристики

Амплитудно-частотной характеристикой (АЧХ) является модуль комплексного коэффициента передачи по напряжению. Следовательно для определения

АЧХ нужно определить модуль от выражения (16). Как известно, модуль комплексной дроби равен модулю числителя делённого на модуль знаменателя. С учётом сказанного АЧХ принимает вид:

. (17)

Далее, в соответствии с заданием, необходимо построить график АЧХ. Для этого следует задавать значения частоты и находить значения АЧХ. Полезно предварительно знать в каких пределах изменяется АЧХ при изменении частоты от нулевого значения до бесконечности. Это поможет определить интервал задаваемых значений частот.

Определение значения АЧХ на граничных частотах можно двумя способами. Один из них состоит в том, что исходная схема заменяется эквивалентной схемой для нулевой частоты и для частоты равной бесконечности. Так как на нулевой частоте сопротивление катушки равно нулю, а сопротивление конденсатора равно бесконечности, то в схеме в место катушки будет перемычка, а в место конденсатора разрыв. В этом случае исходная схема принимает вид, как это показано на рис.15.

Наличие разрыва в место конденсатора приводит к тому, что напряжения на нагрузке не будет, т.е. оно равно нулю. Следовательно, АЧХ на нулевой частоте тоже имеет нулевое значение.

При частоте равной бесконечности сопротивление катушки равно бесконечности, а сопротивление конденсатора равно нулю. В этом случае исходная схема примет вид, представленный на рис.16.

Схема содержит три резистора и определить коэффициент передачи здесь не представляет труда:

Второй способ состоит в том, что в формулу для АЧХ (17) подставляются крайние значения частоты. Так подстановка нулевого значения частоты сразу показывает, что АЧХ на этой частоте равно нулю. Этот способ для нулевой частоты проще предыдущего. Однако необходимо иметь в виду, что полученная формула может быть с ошибкой, которая вкралась в неё в процессе вычислений. Поэтому дублирующая проверка с помощью схемы замещения совсем не бесполезна. К этому следует добавить, при инженерном анализе используется именно этот способ.

Определение значения АЧХ при частоте равной бесконечности по формуле (17) приводит к неопределённости. Можно воспользоваться правилом Лапиталя, но это приведёт к громоздким вычислениям. В таких случаях делают преобразования, в результате которых частота окажется в знаменателе числа. В нашем случае разделим числитель и знаменатель на .

.

При подстановке в это выражение значение частоты равное бесконечности получаем:

Сравнивая результаты значений АЧХ, полученных двумя способами, видим, что они близки и это даёт основание говорить, что формулы (16) и (17) соответствуют нашей схеме.

Теперь, зная предельное значение АЧХ, можно путём подстановки в (16) больших значений частоты найти наибольшее граничное значение частоты, при котором расчётное значение АЧХ будет достаточно близко к предельному значению АЧХ. Считается, что расчётное значение АЧХ достаточно близко к предельному значению, если оно отличается от него на 1%.

рад.	0	1	3	5	7	10	20	30	50	100	500
	0	0,127	0,247	0,299	0,336	0,379	0,437	0,483	0,501	0,508	0,511

Результаты расчёта АЧХ (16) сводятся в таблицу.

По табличным данным строится АЧХ (рис.17).

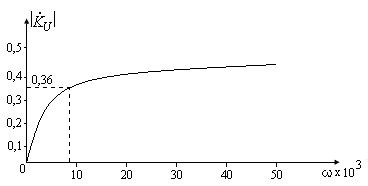
Рис.17 График амплитудно-частотной характеристики.