Задача Штурма — Лиувилля

Задача Шту́рма — Лиуви́лля состоит в отыскании нетривиальных (т.е. отличных от тождественного нуля) решений на промежутке   однородного уравнения

удовлетворяющих однородным граничным условиям

и значений параметра  , при которых такие удовлетворяющие указанным граничным условиям решения существуют.

Оператор   здесь — это действующий на функцию   линейный дифференциальный оператор второго порядка вида

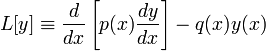
(оператор Штурма — Лиувилля),   — вещественный аргумент.

Функции   предполагаются непрерывными на  , кроме того функции  положительны на  .

Искомые нетривиальные решения называются собственными функциями этой задачи, а значения  , при которых такое решение существует — её собственными значениями (каждому собственному значению соответствует собственная функция).

Свойства

Данная задача обладает рядом свойств:

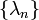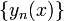• Существует бесконечное счетное множество   собственных значений и соответствующая им бесконечная последовательность   собственных функций. Все собственные значения можно занумеровать в порядке возрастания их абсолютной величины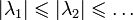 

• Все собственные значения задачи действительные.

• Каждому собственному значению соответствует с точностью до постоянного множителя только одна собственная функция.

• Рассмотрение комплекснозначных собственных функций не обогащает систему всех собственных функций, но добавляет в неё линейно зависимые элементы.

• В случае граничных условий 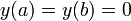  и при выполнении условия 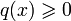  все собственные значениякраевой задачи положительны  .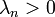

• Собственные функции 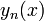  образуют на 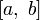  ортогональную с весом 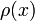  систему  :

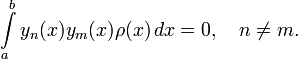
Задача Коши для оду эйлерова типа с постоянными коэффициентами и полиномиальной правой частью. Метод неопределенных коэффициентов.

Если в ЛОДУ эйлерова типа коэффициенты постоянны, а правая часть-полином 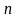-го порядка

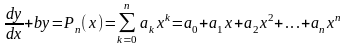(40)

то представляя искомую функцию полиномом того же порядка с неопределенными коэффициентами

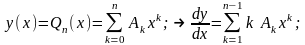(41)

и подставляя ее в уравнение, используя равенство обеих частей редуцированного уравнения по свойству тождественности полиномов

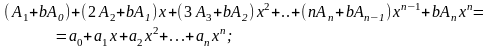(42)

(коэффициенты при одинаковых степенях тождественных полиномов равны) составляется конечная система алгебраических уравнений относительно неопределенных коэффициентов по алгоритму

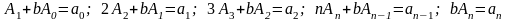(43)

и в результате решения этой последовательно связной системы определяются неопределенные коэффициенты, а, значит, и решение в форме полинома.

4.3.3. Метод ломаных Эйлера. Численный метод, основанный на приближенном представлении ОДУ и использующий дискретную форму представления искомой функции 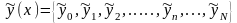в точках разбиения заданного интервала 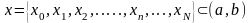, применительно к задаче Коши

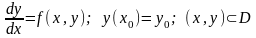(44)

имеет следующую процедуру (алгоритм) построения решения:

-задается сетка-разбиение (дискретизация) аргумента и для нее определяется шаг разбиения

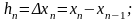(45)

• каждой точке разбиения ставится в соответствие подлежащие

определению дискретные значения функции и ее приращения

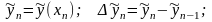(46)

• ограничиваясь линейным представлением производной, определяется

реккурентная формула вычисления искомых значений функции

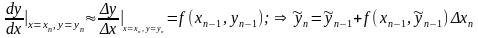(47)

Полученные значения и есть искомое приближенное решение задачи Коши. Точность решения зависит от шага разбиения (чем меньше шаг тем лучше); часто используется постоянный шаг 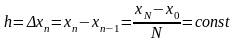и соответствующая реккурентная формула

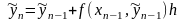(48)

4.3.4. Метод изоклин. Графическое решение задачи Коши для ОДУ первого порядка основано на геометрической трактовки уравнения как углового коэффициента касательной к интегральной кривой

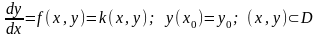(49)

и при фиксированном 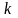описывает кривую с равными углами наклона касательной, называемых изоклинами. Уравнение изоклин

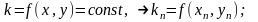(50)

Метод изоклин состоит в построении семейства изоклин с нанесенными на них отрезками касательных. Множество отрезков касательных образует поле направлений касательных интегральных кривых. Алгоритм построения решения таков:

• определяется значение углового коэффициента касательной к

интегральной кривой в начальной точке и задается набор значений углового коэффициента, каждое из значений близки друг другу

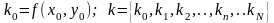
• строится семейство изоклин для каждого значения выбранных угловых

коэффициентов

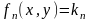
• под углом 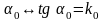строится отрезок касательной до пересечения с

ближайшей кривой семейства ;

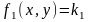• под углом строится отрезок касательной до пересечения с

ближайшей кривой семейства 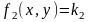и т.д. до достижения точек пересечения отрезков касательных и кривых семейства предельных точек области .

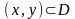Пример 8 (РГР). Показать на рисунке интегральную кривую уравнения

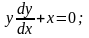проходящую через точку .

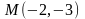Порядок построения:

• уравнению изоклин 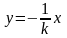- соответствует семейство прямых,

проходящих через начало координат, среди которых начальная, проходящая через начальную точку ;

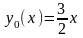- определяется начальное значение 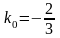углового коэффициента и соответствующий набор, например, ;

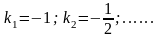• из начальной точки под углом 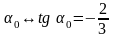строится отрезок

касательной (в рассматриваемом случае он перпендикулярен к изоклине) до пересечения с соседней изоклиной ;

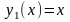- из точки пересечения под углом 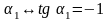строится отрезок

касательной (в рассматриваемом случае он перпендикулярен к изоклине) до пересечения с соседней изоклиной 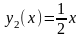и т.д..