Однородная краевая задача для лоду второго порядка с
коэффициентами, зависящими от параметра (задача Штурма-Лиувилля). Собственные числа и собственные функции.
Оп.1. Однородной краевой задачей называется такая задача, для
которой
правая часть краевых условий имеет
нулевые значения, т.е. числа
,
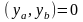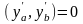или
равны нулю.
Оп.2.
Линейным дифференциальным оператором
второго порядка с коэффициентами,
зависящими от одного числового параметра
,
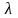называется оператор вида
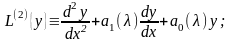(13)
Оп.3. Линейным граничным дифференциальным оператором первого порядка называется опреатор вида
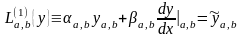(14)
здесь
нижний индекс указывает на принадлежность
к начальному
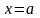или конечному
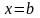значению координат точек интервала.
Оп.4. Однородной краевой задачей для ЛОДУ второго порядка с коэффициентами, зависящими от обного числового параметра, называется краевая задача вида
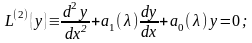(15)
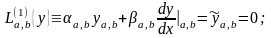(16)
состоящая в определении таких значений парметра , при которых поставленная задача имеет не тривиальное значение (задача Штурма-Лиувилля).
Оп.
5. Значения параметра
,
прикоторых задача Штурма-Лиувилля имеет
решения называются собствеными
значениями
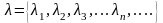или собственными
числами.
Оп.
6. Функции-решения
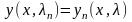задачи Штурма-Лиувилля, соответствующих
собственным значениям (собственным
числам), называ.тся собственными
функциями.
Общая форма простейшей задачи Штурма-Лиувилля является такая, когда коэффициенты дифференциального оператора-степенные функции искомого параметра
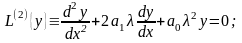
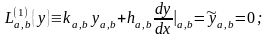(17)
где
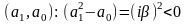- такие числа, дискиминант которых
отрицательное число; это дает
фундаментальные
решения в
виде экспонет
и синус-косинус функций,
т.е. решение в форме
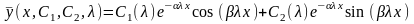(18)
произвольные
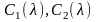постоянные-функции параметра
,
определяемые
из детерминантного
определяющего уравнения,
составленного для заданного типа краевых
условий для каждого фундаметального
решения
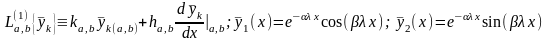(19)
и принимающего форму
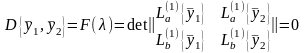(20)
в результате имеем одно трансцендентное (или тригонометрическое) детерминантное характеристическое уравнение для определения значений параметра :
- для краевых условий первого рода на обоих краях
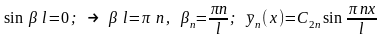(21)
- для краевых условий второго рода на обоих краях
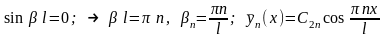(22)
для краевых условий третьего рода на обоих краях
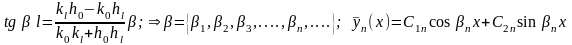(23)
В первых двух случаях имеем тригонометрические уравнения, решения которых простые и дают счетное множество собственных чисел и собственных функций, а в третьем-уравнение трансцендентное, решение может быть определено, например, графически путем построения тангенсоиды и прямо и определения точек пересечения кривых; в результате также имеем счетное множество собственных чисел и собственных функций