Лоду второго пордка с переменными коэффициентами-степенными функциями. Уравнения Эйлера.

6.1.1. Подстановка Эйлера (сведение к ЛОДУ с постоянными коэффициентами). ЛОДУ второго порядка, у которых коэффициенты при производных-степенные функции с показателем равным порядку производной с помощью подстановки Эйлера сводятся к ЛОДУ с постоянными коэффициентами

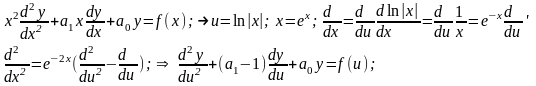(1)

решение которого определяется известными методами, изложенными в предыдущих лекциях.

6.1.2. Метод характеристических показателей степенных фундаметальных решений Эйлера. Полагая фундаментальные решения соответствующих однородных ЛОДУ в виде степенных функций с искомым показателем

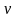
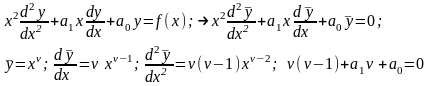(2)

Характеристическое (вековое) определяющее уравнение для чисел -алгебраическое уравнение второго порядка, корням которого

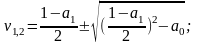(3)

соответствуют следующие фундаментальные решения

• корни действительные простые (некратные)

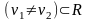
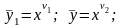(4)

• корни действительные кратные

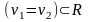
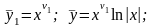(5)

• корни комплксно-сопряженные

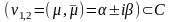
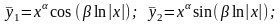(6)

Пример 13 (РГР). Решить уравнение

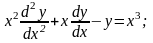
Используем метод подстановки Эйлера-степенных фундаментальных решений, в соответствии с которым однородному уравнению ставится в соответствие вековое уравнение и фундаментальные решения

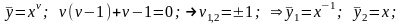
Правая часть специального вида, поэтому частное решение может быть определено методом неопределенных коэффициентов по схеме

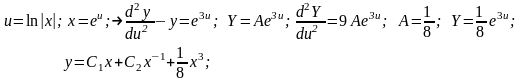
6.2. Общие и частные решения для ОДУ второго порядка. Для ОДУ второго порядка определены три основные типа задач:

-определение общего решения ОДУ на заданном промежутке ;

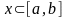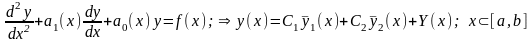(7)

-определение частного решения ОДУ на заданном промежутке , удовлетворяющем начальному условию (условию Коши), когда заданы значение искомой функции и ее производной в заданной точке промежутка

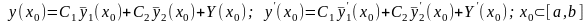(8)

-определение частного решения ОДУ на заданном промежутке , удовлетворяющем граничным условиям (краевым), когда заданы значение искомой функции или ее производной в конечных точках промежутка.

 

Краевая задача для оду второго порядка.

Произвольные постоянные (две) интегрирования в общем решении ОДУ определяются из дополнительных краевых (граничных) условий. Для ЛОДУ второго порядка

(9)

различают три типа линейных краевых условий:

-условия первого рода (Дирихле), когда на краях интервала заданы значения искомой функции

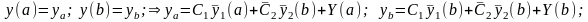(10)

-условия второго рода (Неймана), когда на краях интервала заданы значения производных искомой функции

(11)

-условия третьего рода (Робина или Ньютона), когда на краях интервала заданы линеные комбинации значений искомой функции и ее производных

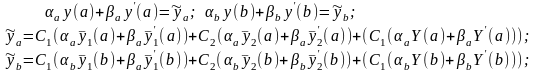(12)

В результате постоянные интегрирования определяются из линейной системы двух алгебраических уравнений, дающей частное решение краевой (граничной) задачи для ОДУ второго порядка.