
- •Задачи коши для линейного оду 1 го порядка.
- •Линейные дифференциальные уравнения высших порядков с постоянными коэффициентами.
- •Лоду второго пордка с переменными коэффициентами-степенными функциями. Уравнения Эйлера.
- •Краевая задача для оду второго порядка.
- •Однородная краевая задача для лоду второго порядка с
- •Задача Штурма — Лиувилля
- •Свойства
- •Задача Коши для оду эйлерова типа с постоянными коэффициентами и полиномиальной правой частью. Метод неопределенных коэффициентов.
Линейные дифференциальные уравнения высших порядков с постоянными коэффициентами.
В
этой статье поговорим о решении линейных
однородных и неоднородных дифференциальных
уравнений порядка выше второго с
постоянными коэффициентами. Такие
уравнения имеют вид ![]() и
и ![]() ,
где
,
где ![]() -
действительные числа, а функция f(x) непрерывна
на интервале интегрирования X.
Сразу
скажем, что аналитически решить такие
уравнения далеко не всегда возможно и
обычно используют приближенные методы.
Однако в некоторых случаях возможно
отыскать общее решение.
Сформулируем
две теоремы, которые показывают, в каком
виде искать общие решения ЛОДУ и
ЛНДУ.
Общим решением y0 линейного
однородного дифференциального
уравнения
-
действительные числа, а функция f(x) непрерывна
на интервале интегрирования X.
Сразу
скажем, что аналитически решить такие
уравнения далеко не всегда возможно и
обычно используют приближенные методы.
Однако в некоторых случаях возможно
отыскать общее решение.
Сформулируем
две теоремы, которые показывают, в каком
виде искать общие решения ЛОДУ и
ЛНДУ.
Общим решением y0 линейного
однородного дифференциального
уравнения ![]() на
интервале X с
непрерывными коэффициентами
на
интервале X с
непрерывными коэффициентами ![]() на X является
линейная комбинация n линейно
независимых частных решений ЛОДУ
на X является
линейная комбинация n линейно
независимых частных решений ЛОДУ ![]() с
произвольными постоянными коэффициентами
с
произвольными постоянными коэффициентами ![]() ,
то есть
,
то есть ![]() .
Общее
решение y линейного
неоднородного дифференциального
уравнения
.
Общее
решение y линейного
неоднородного дифференциального
уравнения ![]() на
интервале X с
непрерывными на том же
промежутке Xкоэффициентами
и
функцией f(x) представляет
собой сумму
на
интервале X с
непрерывными на том же
промежутке Xкоэффициентами
и
функцией f(x) представляет
собой сумму ![]() ,
где y0 -
общее решение соответствующего ЛОДУ
,
а
,
где y0 -
общее решение соответствующего ЛОДУ
,
а ![]() -
какое-нибудь частное решение исходного
ЛНДУ.
Таким образом, общее
решение линейного неоднородного
дифференциального уравнения с постоянными
коэффициентами
ищем
в виде
,
где
-
какое-нибудь его частное решение, а
–
общее решение соответствующего
однородного уравнения
.
Сначала
разберемся как находить
,
а в конце покажем как
определить
.
Уравнение
-
какое-нибудь частное решение исходного
ЛНДУ.
Таким образом, общее
решение линейного неоднородного
дифференциального уравнения с постоянными
коэффициентами
ищем
в виде
,
где
-
какое-нибудь его частное решение, а
–
общее решение соответствующего
однородного уравнения
.
Сначала
разберемся как находить
,
а в конце покажем как
определить
.
Уравнение ![]() называется
характеристическим уравнением линейного
однородного дифференциального
уравнения
.
Если мы найдем все n корней
характеристического уравнения
называется
характеристическим уравнением линейного
однородного дифференциального
уравнения
.
Если мы найдем все n корней
характеристического уравнения ![]() ,
то, исходя из их значений, можно
определить n частных
линейно независимых решений
,
то, исходя из их значений, можно
определить n частных
линейно независимых решений ![]() исходного
ЛОДУ.
Перечислим все возможные
варианты и разберем примеры на каждый
из них:
исходного
ЛОДУ.
Перечислим все возможные
варианты и разберем примеры на каждый
из них:
если все решения характеристического уравнения действительные и различные, то линейно независимые частные решения имеют вид
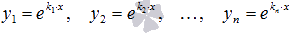 и
и
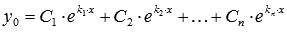 ;
;
если все решения характеристического уравнения действительные и одинаковые
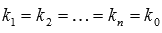 ,
то линейно независимые частные решения
имеют вид
,
то линейно независимые частные решения
имеют вид
 и
и
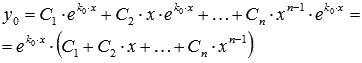
если решениями характеристического уравнения являются различные комплексно сопряженные пары
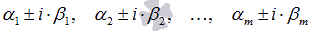 , n
= 2m,
то линейно независимые частные решения
имеют вид
, n
= 2m,
то линейно независимые частные решения
имеют вид
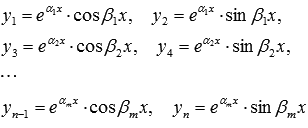 и
и
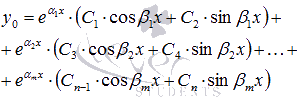 если
решениями характеристического уравнения
являются совпадающие комплексно
сопряженные пары
если
решениями характеристического уравнения
являются совпадающие комплексно
сопряженные пары 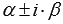 ,
то линейно независимые частные решения
имеют вид
,
то линейно независимые частные решения
имеют вид
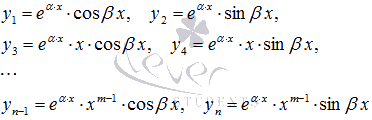 и
и
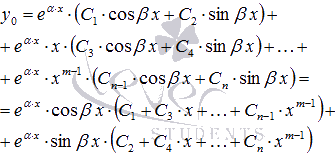
Пример. Найдите общее решение линейного однородного дифференциального уравнения третьего порядка с постоянными коэффициентами
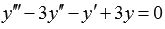 .
Решение.
Запишем
характеристическое уравнение и найдем
его корни, предварительно разложив
многочлен в левой части равенства на
множители способом
группировки:
.
Решение.
Запишем
характеристическое уравнение и найдем
его корни, предварительно разложив
многочлен в левой части равенства на
множители способом
группировки:
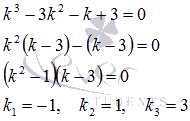 Все
три корня действительные и различные,
поэтому общее решение ЛОДУ имеет
вид
Все
три корня действительные и различные,
поэтому общее решение ЛОДУ имеет
вид
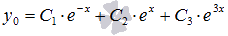 .
.
Пример. Найдите общее решение дифференциального уравнения
 .
Решение.
Характеристическое
уравнение этого ЛОДУ четвертого порядка
имеет вид
.
Решение.
Характеристическое
уравнение этого ЛОДУ четвертого порядка
имеет вид 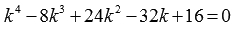 . Если
обратиться к формуле
бинома Ньютона,
то характеристическое уравнение можно
переписать в виде
. Если
обратиться к формуле
бинома Ньютона,
то характеристическое уравнение можно
переписать в виде 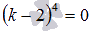 ,
откуда видно его четырехкратный
корень k0 =
2.
Таким образом, общее решение исходного
линейного однородного дифференциального
уравнения с постоянными коэффициентами
есть
,
откуда видно его четырехкратный
корень k0 =
2.
Таким образом, общее решение исходного
линейного однородного дифференциального
уравнения с постоянными коэффициентами
есть
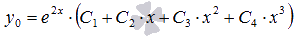 .
.
